#선형대수학은 엄밀한 논리와 추상적인 전개가 주 대상이며 #행렬식, 행렬연산, 행렬의 대각화, 고유값 문제, 선형독립/종속, #선형결합, 선형변환 등이 대상이다.
선형 #대수학 은 #벡터 와 #스칼라 가 무엇인지로 시작하여 #벡터공간 이 무엇인지를 공지8가지로 정의하고 여러 논리를 펼쳐가는 것이 가장 정석적인 선형대수학과정이다.
일반적으로 벡터를 역학에서 기하학적 의미로 정의하여 '크기와 방향이 있는 물리량으로 정의하는데 선형 대수학에서 벡터는 벡터공간의 공리를 만족시키면 그 어떤 대상도 벡터가 될 수 있다.
벡터공간에 대한 개념을 이해하기 위해서는 대수학에서 군, 환, 체가 무엇인지 이해할 필요가 있다. 대수학에서 군, 환, 체의 뼈대를 세우는 일이 매우 중요한 일이지만 개념 자체는 어렵지 않기 때문에 가볍게 터치해 보자.
1. 이항 연산 (Binary operation)
먼저 #연산 (Operation)이 무엇인지 정의해 보자. 4칙연산을 보함하여 적분도 연산의 일종이다. 단지 어떤 대상을 연결시켜 조합을 만들어 내는 행위를 연산의 일종이라고 볼 수 있다. 연산의 정의는 다음과 같다.

쉽게 말하자면 어떤 집합의 두 원소를 뽑아 내서 둘을 연산시켰을 때, 그 연산의 결과물도 집합 X내에 포함된다면 이 연산이 집합에 대해 닫혀 있다(closed)고 말할 수 있다는 것이다.
예를 들어 자연수는 #덧셈 과 #곱셈 에 대해 닫혀 있다. 임의의 #자연수 를 뽑아 덧셈기나 곱셈을 해도 여러번 할지라도 여전히 자연수이기 때문이다. 반면 뺄셈에 대해서는 닫혀있지 않다. 3-5=-2는 자연수가 아니고 5-5=0도 자연수가 아니다.
위 개념은 정의를 기억하고 나서 자연수, #정수 , #유리수 , #무리수 , #실수 에 대해 사칙연산의 닫혀 있는지에 대한 여부 정도로만 확인하고 넘어가도 충분하다.
|
|
N
|
Z
|
I
|
Q
|
R
|
|
+
|
O
|
O
|
×
|
O
|
O
|
|
-
|
×
|
O
|
×
|
O
|
O
|
|
×
|
O
|
O
|
×
|
O
|
O
|
|
÷
|
×
|
×
|
×
|
O
|
O
|
2. 군 (群, Group)
군, 환, 체 중 연산의 기초 중 기초적인 성질이 성립하는 집합을 가리키는 것이 군으로 정의는 다음과 같다.

항등원이란 연산해서 자기 자신을 만드는 어떤 집합의 원소라 볼 수 있다. 함수에서 항등원의 개념은 항등함수이고, 행렬에서는 항등행렬이다. 임의의 행렬에 항등행렬을 무한히 곱해도 여전히 원래 행렬 그대로의 형태가 남기 때문이다. 역원은 항등원의 결과가 나오게 하는 원소로 함수에서 역함수, 행렬에서 역행렬의 역할을 한다.
3. 환 (環, Ring)

#환 은 덧셈 아벨군의 조건을 만족하면서 곱셈에 대한 결합법칙, 분배법칙까지 성립하는 것이고 추가적으로 교환법칙이 성립하면 가환환이라 한다. 정수 전체의 집합 Z와 유리수 전체의 집합 Q, 실수 전체의 집합 R, 복소수의 집합 C가 모두 가환환이다. 곱셈과 덧셈에 대하여 교환법칙이 성립한다.
선형대수학에서 매우 자주 등장하는 행렬은, 행렬의 곱셈의 경우 일반적으로 교환법칙이 성립하지 않는다는 것을 기억하자. MN(R)-n차 정사각행렬, 성분이 환의 원소임을 뜻함-은 가환환이 아닌 환으로 간단히 비가환환이라고 한다.
이렇게 군 > 환 > 체 순서로 어떤 집합의 범위를 좁혀 나가는 것은 연산을 얼만큼 자유자재로 할 수 있는지 적당한 집합을 찾는 것이 목적이기 때문이다. 대수학에서는 사칙연산을 할 수 있는 대상을 찾는 것에 관심이 있기 때문이다. 가장 간단한 덧셈부터 복잡한 나눗셈까지 기본적인 연산법칙들이 성립하는 집합을 찾아 할 수 있다.
4. 체 (Field)
#체 는 가장 중요하고 빈번히 등장하는 연산이 잘 정의되는 집합이다. 체는 사칙연산(나눗셈까지)이 모두 별다른 문제없이 잘 수행되는 대상을 모은 집합이다.
체를 정의하기 전에 곱셈에 대한 역원을 정의해야 한다. R에서 하나 임의로 뽑은 원소에 대해 곱해서 항등원이 되게 하는 원소가 존재할 때, 뽑은 원소를 가역원, 곱해서 항등원을 만드는 원소를 역원이라 한다. 이는 조금만 자세히 들여다 보면 나눗셈을 하겠다는 의도가 깔려 있는 것으로 파악할 수 있다.

체의 정의는 다음과 같다.

유리수 집합 Q, 실수 집합 R, 복소수 집합 C는 모두 체이다. 1에서 설명한 표를 참고하면 좋을 듯 하다. 나눗셈과 정수는 체의 조건을 만족시키지 못한다. 이외에도 체가 되는 집합은 셀수 없이 많은데, 몇가지만 다루어 보도록 합시다.
예제1) 2로 나누었을 때 나머지를 모은 집합 Z2가 Field인지를 검증하여라.
2로 나눈 나머지는 0,1 뿐이므로 Z2의 원소는 이 두개이다.
그럼 0과 1에 대해 각각 ㉡을 만족하는지 확인해 보면 된다. 일단 덧셈과 곱셈을 확인한다.

여기서 왜 1+1이 2가 아니라 0이 되는지 궁금해 할 수 있다. Z2에서 덧셈을 한다는 것은 단순히 더한다는 것이 아니라 더한 숫자를 다시 2로 나누었을 때 나머지가 무엇인지를 확인하는 것이다. 1+1=2를 다시 2로 나누면 나머지가 0이니, Z2에서 1+1은 0이다. 같은 원리로 1+0=1을 다시 2로 나누면 나머지가 1이다. 곱셈 역시 마찬가지다. 그러면 표에서 확인할 수 있듯이 반드시 연산결과가 0 또는 1만 나오게 된다. 이 표를 통해 체의 조건 ㉡이 모두 만족함을 알 수 있다. 예를들어, 1의 덧셈에 대한 항등원은 0이고, 역원은 1이다.
예제2) 다음 집합이 Field임을 보여라.

곱셈에 대한 역원이 존재할까? 역원은 여기서 역수에 해당하는데
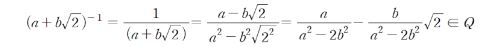
계산해 보면 존재함을 알 수 있다.
이 집합은 Field임을 알 수 있다.
'전기인이 되는 길 > 전기수학' 카테고리의 다른 글
| 미분방정식 : 정의, 용어, 개념 (2) | 2023.07.29 |
|---|---|
| 미분방정식 응용 : 뉴턴 냉각법칙, 리비의 탄소연대 추정 (2) | 2023.07.27 |
| 미분방정식 이해하기 (2) | 2023.07.26 |
| 피벗과 소거법 (Pivots and Elimination method) : 선형 일차 연립방정식 (4) | 2023.02.19 |
| 대칭군, 이면군과 치환 (Symmetric group, Dihedral group, and permutation) (0) | 2023.02.19 |
