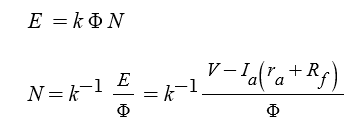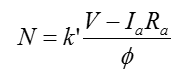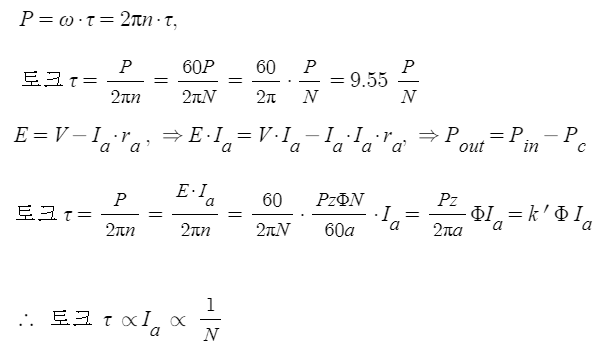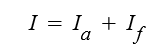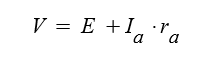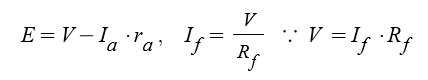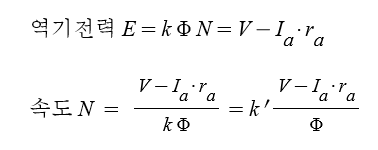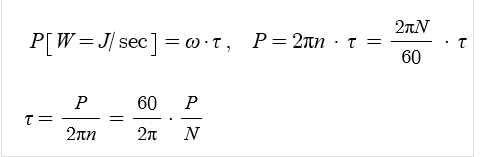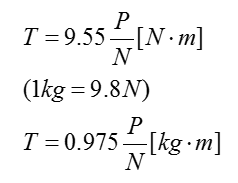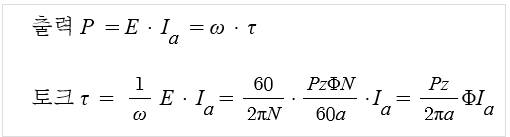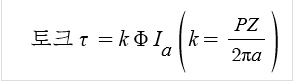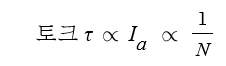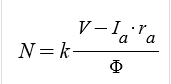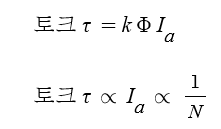이번에는 직류전동의 구조와 원리, 그리고 토크에 대한 개념과 모터에 대해 알아 봅시다.
1. 직류전동기 구조와 원리
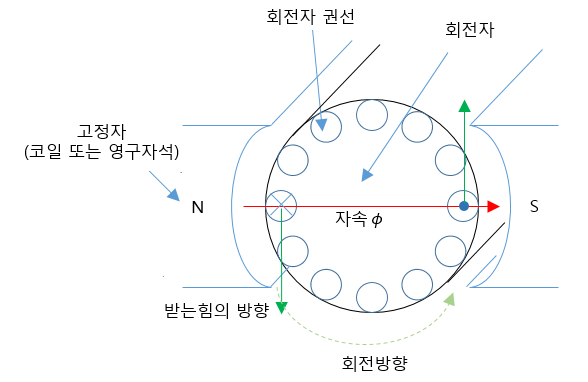 직류전동기 구조
직류전동기 구조
① 직류전동기의 구조
전동기는 발전기와 구조는 동일하다.
전기를 공급하여 회전을 하게 되면 전동기가 되고
회전자(전기자)를 회전시켜서 전기를 만들어 내면 발전기가 되는 것이다.
그렇게 때문에 전기기기를 공부할 때 발전기와 전동기를 분리하지 않고
두 기기를 통칭하여 'Machine'이라고 한다.
기계적 구조는 같지만 발전기와 약간의 용어가 다르긴 합니다.
회전자(Rotor) : 전류가 흐르면 자속에 의해 회전하는 부분(발전기는 전기자)
고정자(Stator) : 자속을 만들어 주는 부분 (발전기는 계자)
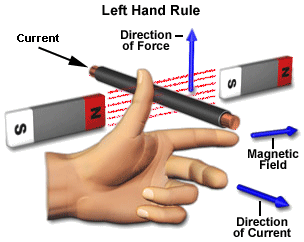
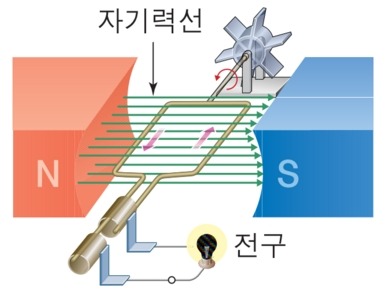
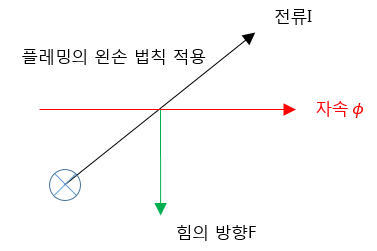 플레밍의 왼손법칙
플레밍의 왼손법칙
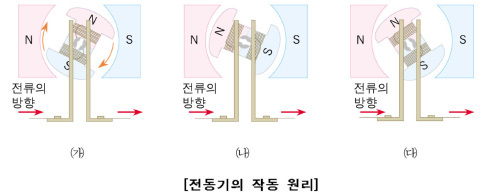
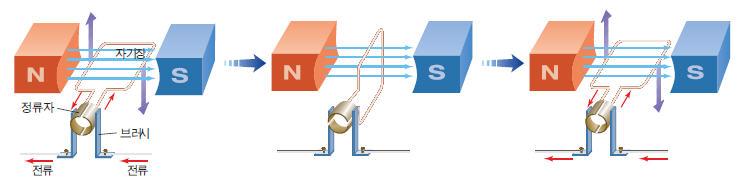
전동기가 회전하는 원리는 플레밍의 왼손법칙을 적용하여 위와 같이 나타낼 수 있습니다.
고정자가 만들어 내는 자속내에 전류가 흐르게 되면 도체에 힘을 받게 됩니다.
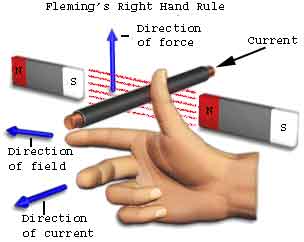
이 때 발전기의 경우 플레밍의 오른손 법칙을 사용하여, 자속에서 전류가 힘을 받으면
전류를 만들어 내게 됩니다.
② 역기전력
전동기가 힘을 받아 회전하는 경우, 그 힘에 의하여 발전기와 같이 기전력을 발생합니다.
이 때 발생하는 기전력은 모터에 입력되는 전압에 반대되는 방향으로 발생하기 때문에
'역기전력'이라고 합니다.
역기전력의 특성은 전동기에 흐르는 전류를 낮추는 역할을 합니다.
역기전력을 이해하기 위해서는 자동차가 빨리 달릴 수록 바람의 저항이 발생하는 것을
상상하면 쉽게 이해할 수 있습니다.
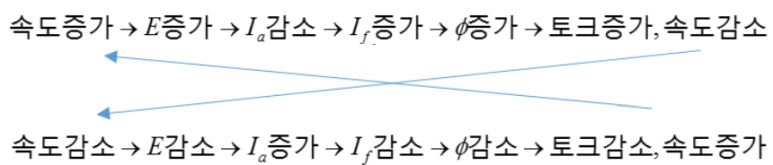
역기전력은 보통 전동기의 회전속도에 따라 증가하게 되는데
전동기가 매우 빠른 속도로 회전할 경우 역기전력과 전동기의 입력전압과 서로 같아져
전류가 매우 작아지는 현상이 발생하게 됩니다.
전동기에 흐르는 전류가 작아지면 고정자의 자속 발생이 작아지고
자속이 낮아지면 전동기 토크가 서서히 떨어지게 되어
결국에는 전동기를 가속하는데 한계가 발생하여
속도에 한계가 발생하게 됩니다.
반대로 전동기의 속도가 낮을 경우에는 역기전력이 작아
매우 큰 전류가 흐를 수 있기 때문에 위험에 처하게 됩니다.
역기전력 : 전동기의 경우 부하로 인해 발전기처럼 동작하여 역으로 기전력이 발생하는 것
③ 전동기 등가회로
전동기는 회전하면서 발생하는 역기전력이 있고
권선에 따라 회전자 권선저항과 고정자 권선저항이 있는 것으로 등가회로를 그릴 수 있다.
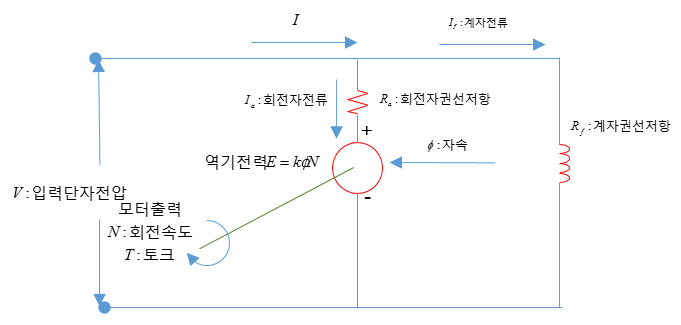
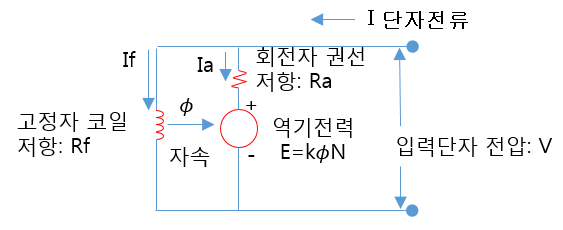
 전동기 등가회로
전동기 등가회로
입력단자에 전압 V를 인가하여 전류가 흐른다고 가정을 합니다.
전동기로 들어가는 전류 I 는 병렬로 나눠지게 되어 Ia 와 If 의 합이 됩니다.
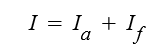
입력전압은 역기전력과 회전자 권선에 걸리는 전압과의 합과 같습니다.
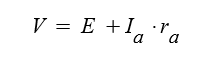
전동기에서 발생하는 역기전력 E와 고정자에 흐르는 전류 If 에 대하여
정리하면 다음과 같습니다.
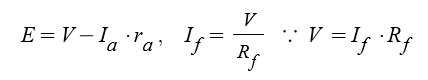
② 토크 공식

⊙ 토크는 회전하는 힘, 돌림힘으로서, 힘(F)와 거리(지레팔)의 곱으로 나타낸다.
이것은 지렛대의 원리와 비슷한 것으로
같은 토크에서 지레팔 거리[m]가 멀수록 힘[F]은 약해지는 특성이 있습니다.
⊙ 만약에 자전거나 자동차를 만들었을 때, 언덕에 오르기 힘들다면,
페달 바퀴를 좀 더 작은 것으로 바꾸어 올라가면 힘이 덜 드는 것과 같습니다.
⊙ 회전하는 물체의 접선의 방향으로 힘이 가해졌을 때,
토크는 회전하는 물체의 중심에서 힘이 작용하는 곳까지의 거리와
힘의 크기의 곱으로 나타냅니다.
따라서 회전하는 돌림힘 토크의 식은 다음과 같습니다.
토크 τ = F × r [N · m]
이때, 1초당 회전수를 초당회전수 n이라고 하면
각주파수와 분당회회전수는 다음과 같다.

⊙ 출력(일률)은 어떤 일을 할 수 있는 능력, 초당 일할 수 있는 능력이라고 할 수 있습니다
즉, 초당 사용하는 에너지를 일률(단위당 일량)이라고 할 수 있습니다.
에너지의 단위는 보통 [J]을 쓰는데, 이 때 1[J]은 1[N]의 힘으로 1[m]를 움직일 때의
에너지를 말합니다.
⊙ 출력 P는 에너지를 시간 초로 나눈 값 [J/sec]이 되며
전기적 단위로 쓰면 1[W] = 1[J/sec]로 나타냅니다.
따라서
에너지 : 1 [J] = 1[N] × 1[m]
일률 : 1[W] = 1[J/sec]
= 1[N] × 1[m] / sec
= 1[N] × 1[m/sec]
⊙ 즉, 힘[N]과 속도 1[m/s]의 곱인 것을 알 수 있습니다.
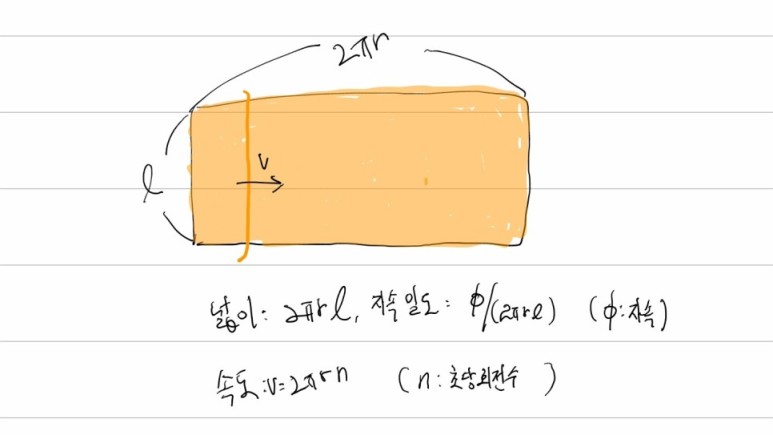
회전하는 물체의 경우 토크가 걸리는 지점의 속도를 계산하면
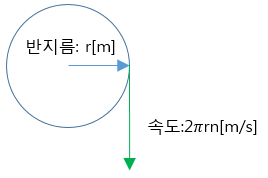
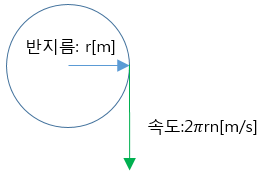
원둘레 길이 : 2πr [m]
1초당회전속도 : n [rps = 회전수/초]
속도 : = 원둘레 × 1초당 회전수 [n/sec]
= 2πr · n [m/s]

[토크와 각속도의 관계]
물체에 힘을 작용하면 물체의 속도가 바뀝니다.
그런데 크기를 갖는 물체의 한부분이 고정되어 있을 때
힘을 작용하면 물체는 회전합니다.
이때 물체의 각속도가 바뀐다고 말합니다.
물체의 속도가 바뀌는 정도 즉 가속도는 물체에 작용한 힘에 비례합니다.
그런데 물체의 각속도가 바뀌는 정도, 각가속도는
단순히 물체에 작용한 힘에만 비례하는 것이 아니라
똑같은 힘을 작용하더라도
물체의 고정된 부분에서 얼마나 멀리 떨어진 곳에 그 힘이 작용했는지에도 비례합니다.
즉 고정된 부분에서 먼 곳에 작용할 수록 각가속도가 커집니다.
이 효과 즉 힘에 고정점에서 힘의 작용점까지 거리를 곱한 것을 토크라고 합니다.
그래서 토크는 "힘 x 회전축에서 거리" 라고 표현할 수 있습니다.
그런데 각속도와 속도 사이의 관계는 "속도 = 각속도 x 회전축에서 거리" 입니다.
따라서 "토크 x 각속도 = (힘 x 회전축에서 거리) x (속도 / 회전축에서 거리) = 힘 x 속도"
즉, 출력(일률[W])은 힘 x 속도 = 토크 x 각속도, P = ω τ " 가 됩니다.
회전수가 분당회전수라면 초당 회전수로 변환하여 사용합니다.
초당회전수 : n[rps], 각 주파수 ω = 2πn = 2πN / 60
분당회전수 : N[rpm], 출력 P = ω τ = 2πN / 60 · τ
⊙ 토크는 회전하는 물체가 회전하기 위한 가속을 위한 힘과 비슷한 요소입니다.
다만, 토크는 힘에 중심에서의 거리가 곱해지는 부분이 다릅니다.
같은 힘이라도 중심(지레점)에서 가까우냐, 머냐에 따라 가해지는 토크가 달라집니다.
반대로 토크를 만들어 내는 모터의 경우
같은 토크라도 힘을 주는 부분이 중심(지레점)에서 가까우냐 머냐에 따라
실제 주는 힘이 달라집니다.
⊙ 모터는 입력되는 Power만큼 기계적 출력을 내기 때문에
입력(P = VI)에 비례하여 출력 (P = 속도 × 힘)이 결정됩니다.
모터의 출력이 크다고 하는 것은 회전속도와 토크가 큰 것이며
이 둘의 곱은 언제나 일정하게 됩니다.
따라서 동일한 모터가 토크가 부족하면 속도를 줄이고
혹은 속도가 부족하면 토크를 줄이도록 하는 방법으로
필요한 성능을 낼 수 있도록 합니다.
⑤ 속도 공식
⊙ 모터의 회전속도는
입력 Power에 따라 회전을 하게 되면서 발생하는 역기전력의 크기로 구할 수 있습니다.
발생하는 역기전력이 클수록 회전속도가 높아 집니다 ( E = kΦN )
⊙ 역기전력이 작아지게 하는 회전자 전류 Ia가 작을 수록,
회전을 방해하는 자속이 작을 수록 회전속도는 커지게 됩니다.
⊙ 모터가 회전하여 발생하는 역기전력은 모터의 입력전압 V와
흐르는 전류 Ia와 회전자 저항 Ra 값을 알고 있을 때 알 수 있습니 다.
역기전력 E = V - Ia · Ra ∵ V = E + Ia · Ra
이 때, E를 알게 되면 다시 역기전력 공식을 통해 회전수를 알 수 있습니다.
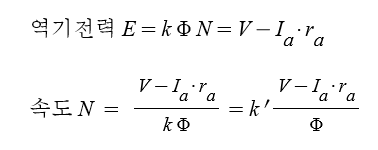
⊙ 비례상수 k' 는 k의 역수로서 계산하기 편하게 다시 쓴 것입니다.
여기서 회전속도는 여러가지 요소들에 의해서 결정되지만,
특히 모터의 자속수에 반비례 한다는 것을 눈여겨 봐야 합니다.

⊙ 또한 모터에 흐르는 전류가 작을 수록 회전수가 증가합니다.
자속수와 반비례하는 이유는 모터의 회전자가 회전을 하면서 만들어 내는
역기전력은 회전자가 돌지 못하게 하는 방향으로 발생합니다.
⊙ 역기전력에 의해 모터가 돌지 못하게 하는 힘은 전자석 처럼 작용하기 때문에,
고정자가 만들어 내는 자속이 클수록 못돌게 하는 힘이 커지게 된다고 볼 수 있습니다.
⊙ 모터가 회전하기 위해서 필요한 토크는 자속이 클수록 커지지만
모터가 회전할 수록 발생하는 역기전력에 의해 속도가 크게 감소하게 됩니다.
이러한 성질을 이용해 자속을 조절하여 모터의 속도와 토크를 조절이 가능합니다.
2. DC 모터의 토크계산
⊙ 이제 본격적으로 DC 전동기의 토크를 계산하고자 합니다.
모터에 입력되는 전압과 전류를 알고 있거나 모터의 출력과 회전속도를 알면
각각의 방법으로 토크를 알아 낼 수 있습니다.
V = E + Ia · Ra
V · Ia = E · Ia + Ia2 · Ra
V · Ia(입력 P), E · Ia (출력), Ia2 · Ra (동손)
출력 P = E · Ia = ω τ
위와 같이 주어졌을 때
* 토크 계산식 1 (모터의 일정 출력 P에서 속도 N과의 관계)
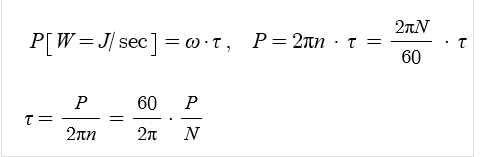
⊙ 출력 P를 알고 있을 때, 토크와 속도와의 관계식을 통해서 위와같이 정리됩니다.
DC 전동기의 토크는 회전수 N에 반비례함을 알 수 있습니다.
* 공식의 단순화 및 단위 변화 (알고 있는 고정된 수는 계수로 전환)
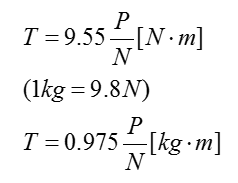
※ 토크 계산식 2 (모터의 전기적 파라미터의 관계식 구하기
(극수,도체수,전류, 자속의 관계 ))
출력 P [W], 회전수 N [rpm]
위와 같이 주어졌을 때, 모터에 입력되는 전압과 전류를 통해
다음과 같이 구할 수 있다.
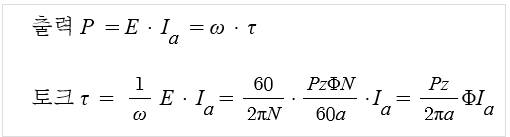
⊙ 여기서 회전수와 무관하게 보이는 식으로 도출되지만
사실상 모터에 흐르는 전류 Ia와 회전수 N은 서로 반비례의 관계이기 때문에
속도와 무관하지 않습니다.
자속과 전류 Ia를 제외하고는 극수 P, 도체수 Z, 병렬 회로수 a는
모터가 설계되어 만들어 진 후에는 고정된 값이 되므로
하나로 묶어 k 상수로 사용하여 간단하게 쓸 수 있습니다.
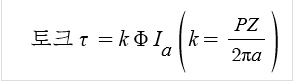
⊙ 토크 계산식 1과 2에서 다음 식을 도출할 수 있다.
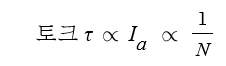
⊙ 결론은 같네요
* DC모터의 토크는 부하(전류)가 클수록 속도가 작을 수록 커짐
3. 타여자 전동기
⊙ 타여자 전동기는 DC 전동기에서 여자를 공급하기 위한 고정자 권선의 입력을
외부에서 가져오는 전동기이며 타여자 발전기와 같은 모양입니다.
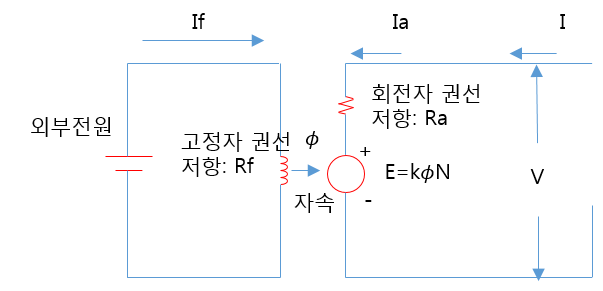
① 속 도
⊙ 모터의 속도는 권선에서 발생하는 자속과
입력되는 전압, 전류와의 관계식으로 다음과 같이 구할 수 있다.
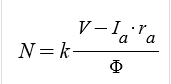
⊙ 위 식을 통해 고정자 권선 저항 Rf에 따라 모터의 속도를 증가시키거나
감소시킬 수 있다.
Rf ↑ ⇒ If ↓ ⇒ Φ ↓ ⇒ N ↑,
Rf ↓ ⇒ If ↑ ⇒ Φ ↑ ⇒ N ↓,
② 토크
⊙ 위에서 토크공식을 이용하여 다음과 같은 결론을 얻었다.
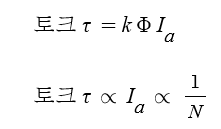
⊙ 타여자 전동기의 토크는 부하 및 속도에 따라 결정됩니다.
③ 용도
⊙ 타여자 전동기는 고정자 권선저항을 조절하여 모터의 속도 및 토크를
쉽게 조절할 수 있습니다.
⊙ 다른 모터들은 별도의 저압조정장치와 같은 복잡한 제어용 인버터가 필요한
것과 대비됩니다. 따라서 일정한 속도나 일정한 토크의 출력이 용이합니다.
⊙ 타여자 발전기의 단점은 외부의 별도 전원이 필요하다는 것입니다.
※ 사용용도 : 엘리베이터, 압연기
(* 제어가 간단하여 부하변동에도 일정한 속도, 토크 출력이 쉽다는 장점 이용)