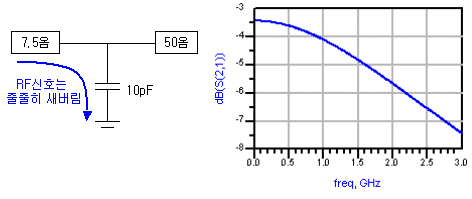
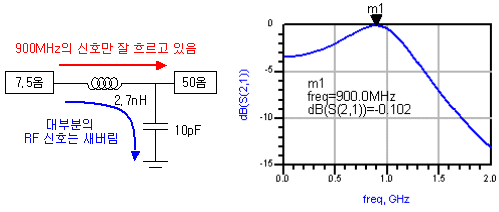
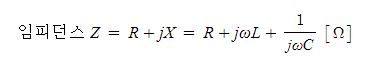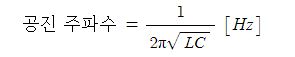제1과목 : 전기이론
1. 도체에 대전체를 접근시키면 대전체에 가까운 쪽에서는 대전체와 다른 전하가 나타나며 그 반대쪽에는 대전체와 같은
종류의 전하가 나타나는 현상이 일어난다. 이와 같은 현상을 무엇이라고 하는가 ?
① 정전 차폐 ② 자기 유도 ③ 대전 ④ 정전유도
[해설] 정전유도 현상 : 대전체를 도체의 근처에 가까이 했을 경우에 대전체 가까운 쪽에는 다른 종류의 전하가, 먼 쪽에는
같은 종류의 전하가 나타나는 현상
2. 도면과 같이 공기 중에 놓은 2 × 10-8 C의 전하에서 4m 떨어진 점 P와 2m 떨어진 점 Q와의 전위차는 몇 V인가 ?

① 45 V ② 40 V ③ 125 V ④ 150 V
[해설] 전위는 거리에 반비례한다.

3. 자계의 영향을 받지 않아 자화가 되지 않는 물질로 강자성체 이외의 자성이 약한 물질이나 전혀 자성을 갖지 않는 물질
을 무엇이라고 하는가 ?
① 상자성체 ② 반자성체 ③ 비자성체 ④ 페리자성체
[해설] 비자성체 (Non-magnetic meterial : 非磁性體)
㉠ 자계에 영향을 받지 않아 자화가 되지 않는 물질로 상자성 물질과 반자성 물질을 포함한다.
㉡ 그 비투자율은 1에 가까운 값이며, 자계에 의해 거의 힘을 받지 않는다. Al, Cu, Sn (주석 등)
※ 폐리 (ferri) 자성체 : 외부 자기장 속에서 자기장과 같은 방향으로 강하게 자화되는 물체를 말하며 텔레비젼이나 반송
전파, 컴퓨터, 마이크로파 기기, 자기 변형 발전기, 고주파 기기에 널리 쓰인다.
4. 길이가 31.4 ㎝, 단면적 0.25 ㎡, 비투자율이 100인 철심을 이용하여 자기회로를 구성하면 자기저항은 몇 AT/Wb인가 ?
(단, 진공의 투자율은 μo = 4π × 10-7 H/m로 계산한다.)
① 2648.24 ② 6784.58 ③ 8741.49 ④ 9997.53
[해설]
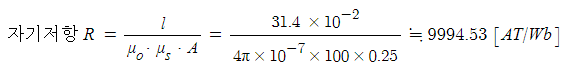
5. 공기중에 1 m 떨어져 평행으로 놓인 두 개의 무한히 긴 도선에 왕복 전류가 흐를 때, 단위 길이 당 18 × 10-7 [N]의 힘이
작용한다면 이 때 흐르는 전류는 약 몇 A인가 ?
① 3 ② 9 ③ 27 ④ 34
[해설] 도체간 작용하는 힘

6. 자장 중에서 도선에 발생하는 유기기전력의 방향은 어떤 법칙에 의하여 설명되는가 ?
① 페러데이 (Fareday)의 법칙 ② 앙페르(Ampere)의 오른나사 법칙
② 렌츠 (Lenz)의 법칙 ④ 가우스 (Gauss)의 법칙
[해설] 렌츠의 법칙 (Lenz's law) : 전자 유도에 의하여 생긴 기전력의 방향은 그 유도 전류가 만드는 자속이 항상 원래 자속
의 증가 또는 감소를 방해하는 방향으로 작용한다.
7. 어느 코일에서 0.1초 동안에 전류가 0.3 A에서 0.2 A로 변화할 때 코일에 유도되는 기전력이 2 × 10-4 V 이면, 이 코일의
자체 인덕턴스는 몇 mH인가 ?
① 0.1 ② 0.2 ③ 0.3 ④ 0.4
[해설] 전자기 유도 기전력

8. 두 코일이 서로 직각으로 교차할 때 상호 인덕턴스는 ?
① L1 + L2 ② L1 - L2 ③ L1 × L2 ④ 0
[해설] 두 코일이 직각 교차하므로 서로 쇄교되는 자속이 없으므로 상호인덕턴스는 "0"이다.
9. 주파수 10 Hz의 주기는 몇 초인가 ?
① 0.05 ② 0.02 ③ 0.01 ④ 0.1
[해설] 주기 = 1/주파수, T =1/f =1/10 = 0.1 [s]
10. L만의 회로에서 유도 리액턴스는 주파수가 1 kHz일 때 50 Ω 이었다. 주파수를 500Hz로 바꾸면 유도 리액턴스는
몇 Ω 인가 ?
① 12.5 ② 25 ③ 50 ④ 100
[해설] 유도리액턴스 : XL = 2πf·L [Ω] 에서, 주파수 f가 1/2배로 되면 XL도 1/2배가 된다.
11. R = 8 Ω, L = 19.1 mH의 직렬 회로에 5A가 흐르고 있을 때 인덕턴스 (L)에 걸리는 단자전압의 크기는 약 몇 V인가 ?
(단, 주파수는 60 Hz이다.)
① 12 ② 25 ③ 29 ④ 36

12. 전압 200 V, 저항 8 [Ω], 유도 리액턴스 6 Ω 이 직렬로 연결된 회로에 흐르는 전류와 역률은 얼마인가 ?
① 20 A, 0.8 ② 20 A, 0.7 ③ 10 A, 0.6 ④ 10 A, 0.5

13. 저항 4 Ω, 유도 리액턴스 8 Ω, 용량 리액턴스 5 Ω 이 직렬로 연결된 회로에서의 역률은 얼마인가 ?
① 0.8 ② 0.7 ③ 0.6 ④ 0.5

14. RLC 직렬 공진 회로에서 최대가 되는 것은 ?
① 전류 ② 임피던스 ③ 리액턴스 ④ 저항
[해설] 직렬 공진 시 임피던스가 최소가 되므로, 전류는 최대가 된다.
15. RC 병렬 회로의 임피던스는 ?

16. 다음 중 유효전력의 단위는 어느 것인가 ?
① W ② Var ③ kVA ④ VA
[해설] ㉠ 피상전력 : VA (Volt-ampere), kVA, MVA
㉡ 무효전력 : var, kvar, Mvar
㉢ 유효전력 : W, kW, MW
17. 220 V 용 50 W 전구와 30 W 전구를 직렬로 연결하여 220 V의 전원에 연결하면 ?
① 두 전구의 밝기가 같다. ② 30 W의 전구가 더 밝다.
③ 50 W의 전구가 더 밝다. ④ 두 전구 모두 안 켜진다.
[해설] 직렬 연결시 두 전구에 흐르는 전류는 같으므로 내부 저항이 큰 30 W의 전구가 더 밝다. (P = I2R [W])

18. 평형 3상 회로에서 1상의 소비전력이 P라면 3상 회로의 전체 소비전력은 ?

[해설] 각 상에서 소비되는 전력은 평형 회로이므로 Pa = Pb = Pc
∴ 3상의 합계 소비전력 P = Pa + Pb + Pc = 3P [W]
19. 세변의 저항 Ra = Rb = Rc = 15 Ω 인 Y결선회로가 있다. 이것과 등가인 △결선 회로의 각 변의 저항은 몇 Ω 인가 ?
① 5 ② 10 ③ 25 ④ 45

20. 비정현파가 발생하는 원인과 거리가 먼 것은 ?
① 자기 포화 ② 옴의 법칙 ③ 히스테리시스 ④ 전기자 반작용
[해설] 비정현파가 발생하는 원인
㉠ 정현파 교류는 기전력이 정현파가 아닌 경우에 발생하는 것 외에 회로 내에 비선형 (nonlinear) 소자가 있는 경우에
발생한다.
㉡ 비선형소자에는 옴 (Ohm)의 법칙을 따르지 않는 인덕턴스나 콘덴서 또는 능동소자로서 진공관, 트랜지스터 등이
있다.
㉢ 코일이 철 등과 같은 강자성체에 감겨 있는 경우에는 자성재료 포화특성 및 히스테리시스 특성에 의하여 전류의 파형
이 일그러지게 된다.
[정답] 1. ④ 2. ① 3. ③ 4. ④ 5. ① 6. ③ 7. ② 8. ④ 9. ④ 10. ② 11. ④
12. ① 13. ① 14. ① 15. ④ 16. ① 17. ② 18. ③ 19. ④ 20. ②
#정전유도 #대전 #전위 #강자성체 #투자율 #자기회로 #기전력 #코일 #인덕턴스 #주파수 #리액턴스 #역률 #공진 #직렬공진 #유효전력 #비정현파 #히스테리시스 #비선형
'전기기능사' 카테고리의 다른 글
| 전기기능사 필기 모의고사 2-3 (0) | 2024.01.20 |
|---|---|
| 전기기능사 필기 모의고사 2-2 (0) | 2024.01.19 |
| 전기기능사 필기 모의고사 1-2 (2) | 2024.01.17 |
| 전기기능사 필기 모의고사 1-1 (0) | 2024.01.17 |
| 전기기능사 모의 고사 1 (2) | 2024.01.16 |