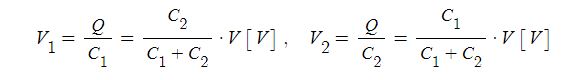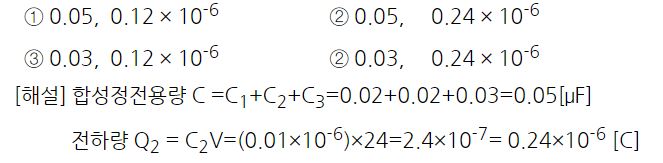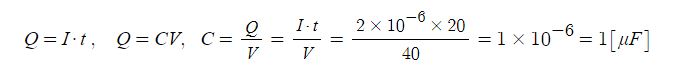1. 상호 #인덕턴스
두개의 코일을 가까이 하고 한쪽 코일에 전류가 흐르게 하면 전류가 흐르는 코일에는 자기장이 발생하게 된다.
이 #자기장 은 전류가 흐르지 않는 코일에도 영향을 주어 전류가 흐르지 않는 #코일 은 #자속 발생을 억제하는 방향으로
기전력이 발생하는데 이렇게 한쪽 코일의 자기장이 다른 쪽 코일에 영향을 주어 기전력이 발생하도록 하는 것을
상호인덕턴스라고 한다.
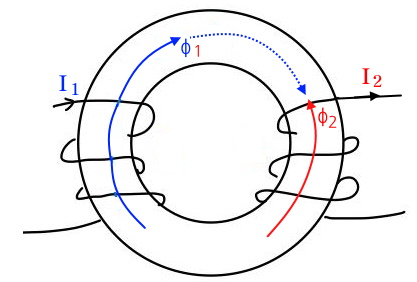
위 그림과 같이 환상 솔레노이드에 2개의 코일이 감겨져 있다.
왼쪽 코일에 전원에 연결되어 외부에서 전류를 흐르게 하고 오른 쪽 코일에는 전원이 연결되어 있지 않다.
왼쪽 코일에는 외부 전원에 의해 전류가 흘러 자기 인덕턴스에 의해 자속이 발생하고 이 자속은 환상 솔레노이드를 통해
오른쪽 코일에 전달된다. 오른 쪽 코일은 이 자속의 변화를 방해하기 위한 자속을 발생하게 되고 이것은 기전력이 되어
오른쪽 코일에도 기전력이 발생하게 된다. 이를 식으로 표현하면 다음과 같다.

상호 #인덕턴스 에 의해 e2는 다른 코일의 전류에 의해 기전력이 발생하게 된다.
2. 인덕터의 #직렬 연결
가. 상호인덕턴스가 존재하지 않을 때
▣ 상호 인덕턴스가 존재하지 않는다면 2개의 인덕터는 각각 독립적으로 역할을 한다
▣ #인덕터 를 직렬로 연결하면 인덕터는 회로에서 저항과 같이 임피던스 역할을 하게 되므로 직렬회로에서는
전류는 일정하고 전압이 각 인덕터에 분배된다.
▣ 이를 이용하여 두개의 인덕터에 발생하는 합성 인덕턴스를 구할 수 있다.
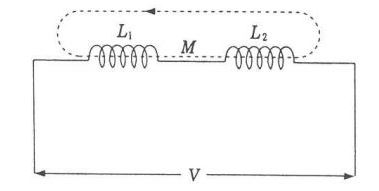
▣ 합성 #전압 V 는 각각의 코일에 발생하는 전압의 합이므로 다음식이 성립된다.

나. 상호인덕턴스가 존재할 때
① #가동결합
▣ 아래 그림과 같이 두 코일이 감긴 방향이 같은 경우 L1에 흐르는 전류가 다른 코일 L2 에 영향을 주고
L2에 발생한 기전력은 다시 L1에 영향을 주게 되어 상호 인덕턴스가 커지게 된다.

합성인덕턴스는 직렬 연결이기 때문에 저항의 직렬연결과 같이 전압분배식을 이용한다.

② #차동 결합
▣ 아래 그림과 같이 두 코일이 감긴 방향이 같은 경우 L1에 흐르는 전류가 다른 코일 L2에 영향을 주고 L2에 발생한
기전력은 다시 L1에 영향을 주게 되어 상호 인덕턴스가 작아지게 된다.

합성인덕턴스는 직렬 연결이기 때문에 저항의 직렬연결과 같이 전압분배식을 이용한다.

합성인덕턴스를 구하는 식은 다음과 같다.

나. 상호 인덕턴스가 존재할 때

4. 전자에너지
가. 코일에 축적되는 #에너지 (W)
코일에 전압을 인가하여 전류를 흘리면 '자속(磁束)'이라는 것이 발생한다. 자석의 자속과 같은 자속이 발생한다.
이 자속은 외부 전원을 차단하여도 그대로 유지되는데 이는 코일에 전류를 흐르게 함으로써 코일이 자화된 것을 의미한다. 즉, 전기에너지가 자기에너지로 변 화하여 코일 내부에 축적된 것이다.
단위 전류당 자속을 생성하는 능력을 '인덕턴스'이라고 합니다. 축적되는 자기에너지의 양이 인덕턴스에 의해 결정되며
단위는 헨리(H)이다.
▣ 에너지를 구하는 식은 W = VI 이다. 여기서 W : 에너지, V : 전압, I : 전류이다.
▣ 위의 에너지는 일반적인 에너지로 회로 전체 에너지를 말하며 전계 내에서 전하를 이동 시킬 때 필요한 에너지를
말한다. 하지만 우리가 구하고자 하는 것은 코일에 축적되는 에너지이다. 코일에 축적되는 에너지는 어떻게 구할까 ?
코일에 축적되는 에너지는 일반 에너지처럼 W = VI로 구할 수 없다. 왜냐하면 코일 내에서는 전류가 일정하지 않으므로
변하는 값이기 때문이다. 이러한 변화하는 값의 합을 구하기 위해서는 적분을 이용하여 구하여야 한다.

나. 단위 #체적당 축적되는 에너지 (Wm)
▣ 에너지는 일을 할 수 있는 능력을 말하며 포텐셜 에너지 즉, 정전계에서는 #기전력, #정자계 에서는 기자력을 의미하며
코일이 저장하는 에너지는 자화되어 자속을 발생할 수 있는 잠재적 기자력을 의미하며 전자석의 공극에 미치는 힘을
말하고 다음과 같다.
▣ 코일이 만드는 전자석의 힘, 기자력과 단위 면적당 축적되는 에너지

▣ 공극에서 단면적이 A[㎡]인 전자석에 자속밀도 B[Wb/㎡]인 자속이 발생했을 때 철편을 흡인하는 힘(기자력)은
다음과 같다.

【출제 예상 문제】
1. A-B 양단에서 본 합성인덕턴스는 ? (단 코일간의 상호유도는 없다고 본다) ③

① 2.5 [H] ② 5 [H] ③ 10 [H] ④ 15 [H]
[해설] 합성인덕턴스
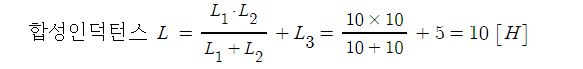
2. 인덕턴스 L[H]인 코일에 I[A]의 전류가 흐른다면 이 코일에 축적되는 에너지 [J]는 ? ③

3. 자기인덕턴스 5[mH]의 코일에 4[A]의 전류를 흘렸을 때 여기에 축적되는 에너지는 얼마인가 ? ②
① 0.04 [W] ② 0.04[J] ③ 0.08[W] ④ 0.08[J]
[해설] 코일에 축적되는 에너지 [J]
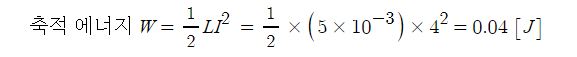
4. 자계의 세기 H[AT/m], 자속밀도 B [Wb/㎡], 투자율 μ[H/m]인 곳의 자계의 에너지 밀도 [J/㎥]는 ? ④

5. #비투자율 이 1,000인 철심의 자속밀도가 1[Wb/㎡]일 때, 이 철심에 축적되는 에너지의 #밀도 [J/㎥]는 ? ②
① 300 ② 400 ③ 500 ④ 600
[해설] 단위 체적당 축적되는 에너지

6. 변압기 철심의 단면적 A=5[㎠], 길이 ℓ=50[㎝], 비투자율 μs= 1,000 코일의 감은 횟수 N=200 이라 하고 1[A]의 전류를
흘렸을 때 자계에 축적되는 에너지는 몇 [J]인가? [단, #누설자속 은 무시한다) ④

'소방설비기사 (전기) > 소방전기일반' 카테고리의 다른 글
| 교류회로의 기본 소자 : 수동 소자 (0) | 2023.02.11 |
|---|---|
| 교류 회로의 기초 (0) | 2023.02.11 |
| 자기유도 (Self induction) 작용과 상호 유도 작용 (0) | 2023.02.08 |
| 전자 유도 현상 : 패러데이의 법칙 등.. (0) | 2023.02.07 |
| 전자력 : 자기장 내에서 도체가 받는 힘 (0) | 2023.02.06 |