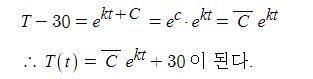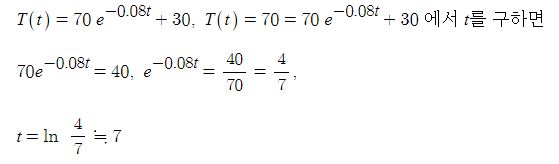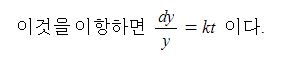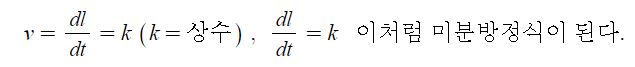아낌없이 주는 나무

미분의 개념을 이야기할 때 미분계수는 어떤 함수의 특정점에서 접선의 기울기값이라고 했다.

특정 점에서 접선의 기울기를 구하기 위하여 극한값을 구하는 과정도 알아 보았다.

그런데 함수 y = f(x)에 대하여 f'(1), f'(2), f'(3) … f'(100)을 구한다면 미분계수의 정의

를 이용하여 미분값을 구한다면 평균변화율의 극한값을 100번을 계산하여야 하는데 이는

번거롭고 효율적이지 못하다. 이런 경우에 x에서의 f'(x)를 함수값으로 하는 새로운 함수

y = f'(x)를 구하여 x값을 대입하면 보다 효율적으로 미분값을 계산할 수 있다.

이와 같이 어떤 함수 y = f(x) 함수에서 x값에 있어서의 미분값으로 하는 새로운 함수

y = f' (x)를 y = f(x)의 도함수라고 한다.

​

1. 도함수의 뜻

​

가. 도함수의 정의

함수 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는​

따라서 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는 a의 값을 2배하여 구할 수 있다. 즉,

f'(1) = 2, f'(√2) =2 √2, f'(π) = 2π, … f'(x) = 2x 이다.

일반적으로 함수 y = f(x)가 정의역 X에서 미분가능하면 정의역에 속하는 모든 x에 대하여

미분계수 f'(x)를 대응시키는 새로운 함수​

이를 그림으로 나타내면 다음과 같다.

이 때, 함수 f'(x)를 f(x)의 도함수라고 하고, 이것을 기호로

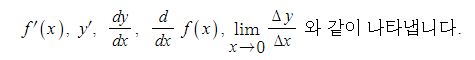
함수 y = f(x) 에서 그 도함수 f'(x)를 구하는 것을 함수 y = f(x)를 x에 대하여 미분한다고 하고 그 계산법을 미분법이라고

한다.​

【평균변화율, 미분계수, 도함수의 비교】

함수 y = f(x) 에서​

   ① 구간에서 x의 증분과 y의 증분의 비율

   ② 기하학적 의미 : 두 점 P(a, f(a), Q (b, f(b))를 지나는 직선의 기울기​

   ① 특정한 값 x = a 에서 평균변화율의 극한

   ② 기하학적 의미 : 곡선 y = f(x) 위의 점 P(a, f(a) 에서의 접선의 기울기​

   ① 특정값이 아닌 정의역에 속하는 임의의 x에 대한 미분계수 함수

   ② 기하학적 의미 : 곡선 y = f(x) 위의 임의의 점 (x, f(x))에서의 접선의 기울기

​

2. 미분법의 공식

도함수의 정의에서 도함수가 존재한다면 주어진 함수의 도함수를 구할 수 있게 된다.

그런데 도함수를 구할 때 정의에 의한 극한의 식으로 도함수를 구하기는 번거롭게 복잡

하다. 따라서 도함수를 구할 때 정의에 의해서 구하는 것보다 공식으로 도함수를 구하면

쉽고 편리하게 구할 수 있다.

​

가. 도함수의 정의에 이용하여 함수 f(x) = xn (n은 양의 정수)의 도함수를 구해 보자.​

인수분해 하면​

나. 상수함수 f(x) = C (C는 상수)의 도함수는

상수함수는 모든 점에서의 접선의 기울기가 항상 0이라는 것을 알 수 있다.

한편 아래의 미분법의 공식과 함수 y = xn 의 미분법을 이용하면 도함수의 정의를 이용하지

않더라도 다항함수​

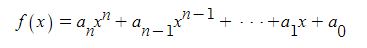
의 도함수를 구할 수 있다.

【미분법의 도함수】

 두 함수 f(x), g(x)의 도함수가 존재할 때

   ① y = cf(x) 이면 y' = c f'(x) (단, c 는 상수)

   ② y = f(x) ± g(x) 이면 y' = f'(x) ± g'(x) (복부호 동순)

   ③ y = f(x) g(x) 이면 y' = f'(x) g(x) + f(x) g'(x) 가 된다.

또한 세함수 f(x), g(x), h(x)가 미분가능하면 함수 y = f(x) g(x) h(x) 도 미분가능하고

y' =f'(x) g(x) h(x)+ f(x) g'(x) h(x)+ f(x) g(x) h'(x) 이다.

​

다. 구간별로 정의된 함수의 도함수

구간별로 정의된 함수

f(x)= x (x < 0), x3 (x≥0) 의 도함수를 구할 때

각 구간의 도함수를 구하여 다음과 같이 나타내는 잘못을 해서는 안된다.

f'(x) = 1 (x <0), 3x2 (x ≥0)

구간의 경계가 되는 x = 0에서 평균변화율의 우극한은 0, 좌극한은 1로 같지 않기 때문에

x = 0 에서의 미분계수는 존재하지 않게 된다.

따라서 아래와 같이 나타내야 한다.

f'(x) = 1 (x <0), 3x2 (x >0)

일반적으로 구간별로 정의된 함수가 주어졌을 때, 그 구간의 경계점에서의 미분가능성은 알

수 없다. 경계점에서 미분가능하려면 미분계수가 존재해야 한다. 즉, 경계점에서의 평균변

화율의 극한이 존재해야 하므로 반드시 우극한과 좌극한이 서로 같은지 확인해야 한다.

참고로​

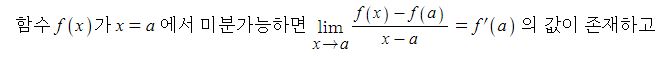
x = a 를 기준으로 나눠서 정의된 다항함수에서의 기하학적인 의미의 y = f(x)의 그래프가

x = a 에서 이어져 있고, 우극한에서의 접선의 기울기와 좌극한에서의 접선의 기울기가

같아야 한다.

​

#도함수 #비분 #우극한 #좌극한 #기하학 #다항함수 #기울기 #미분계수 #함수 #경계점

#평균변화율 #극한 #접선 #정의역 #방정식 #상수 #상수함수

​

【 뉴톤의 냉각법칙 】

​

커피온도는 몇 [℃]일 때 가장 맛이 있을까 ?

커피는 맛으로 마시는 게 아니라 멋으로 마시는 것일 수 있지만 일반적으로 70 [℃]라고

한다. 그럼 100[℃]의 커피를 맛있게 먹으려면 얼마나 기다려야 하는지 알아 보자.

뉴턴의 냉각법칙에 따르면 냉각속도 즉, 온도의 변화속도는 dT/dt는 냉각되는 물체의

온도 T와 주변의 온도 T주변온도 와의 차이에 비례한다.

이것을 식으로 나타내면 다음과 같다.​

이처럼 미분방정식이 성립된다.

이제 100 [℃]의 커피를 30[℃]의 방에 놨을 때 마시기 좋은 온도가 될 때 까지는 몇 분이나

기다려야 하는지 계산해 보자.​

T(t)를 구하기 위해 양변을 적분을 하게 되면​

위 식은 분류를 잘못했다. T는 시간에 따라 변화하는 시간 t의 함수인데

위 식에서는 우변 시간 T를 상수 취급을 하는 오류를 범했다.

온도 T와 시간 t를 따로 모아서 적분을 해야 한다.​

위 식을 적분을 해서 소요되는 시간을 계산해 낼 수 있겠다.​

분모를 미분한 것이 분자에 있으면 ln l분모l가 된다. 위식은 다음과 같이 변한다.​

정리하면 ln lT-30l = kt + C가 되니까.

이제 상수 C를 구해야 하는데 초기조건을 사용하면 된다.

처음(t=0) 커피온도가 100[℃] 즉 T(0)=100 이니까​

하지만 지금도 시간을 구하려 하니 상수 k가 있어서 조건이 하나 더 필요로 한다.

조건하나를 더 추가해 보자. 커피를 놔 두고 3분이 지났더니 커피온도가 85[℃]가

되었다고 하자. 그러면 k를 구할 수 있겠다.​

이제 커피가 70[℃]까지 식는데 소요되는 시간을 구할 수 있겠다.

커피가 100[℃]에서 70[℃]로 식는데는 약 7분 정도 소요되겠다.

​

【 리비의 탄소연대 추정정】 - 방사성 물질의 붕괴

​

탄소연대추정법은 물질속에 C14와 C12의 구성비를 근거로 방사성 동위원소인 C14의 반감기를 추정하여 연대를 추정하는 것이다.

생물의 경우 사체 내에 있는 C14와 C12의 구성비로 연대를 추정한다.

공기중에는 C14와 C12의 구성비율이 일정하다. 식물이건 동물이건 살아있는 동안에는 호

흡을 광합성 또는 음식물 섭취를 통하여 동일한 비율을 유지한다. 그런데 생물이 죽으면 호

흡이나 음식물 섭취가 중단되어 탄소공급이 끊긴다. 그런데 생물이 죽으면 C14 는 방사성

동위원소이니까 스스로 붕괴를 하지만 C12는 그대로 남아 있게 된다. 따라서 세월이 흐르

면 C14 대 C12의 구성비가 변하게 된다.

따라서 생물의 사체내에 존재하는 C14의 양이 공기중의 C14에 비해 몇 [%]나 감소했는

지 알게 되면 생물의 사망연대를 추정할 수가 있다.

그럼 어떤 생물의 사체에서 생존했을 때 있어야 할 C14의 양보다 20[%]밖에 남아 있지

않았다면 이 사체의 사망시점이 몇년 전인지 알아 보자.

C14 는 방사성동위원소로서 붕괴속도는 현재 질량에 비례한다. 이것을 미분방정식으로

나타내면 현재의 질량을 y라 하면 dy/dt =ky이 된다.​

양변에 적분을 해보자.

사망시점 t=0 에서 질량을 yo라고 하면 y(0)= yo 가 된다.​

비례상수 k를 구하기 위해서는 조건이 하나더 주어져야 한다.

또하나의 조건은 C14의 반감기는 5730년이다. 반감기는 질량이 반으로 줄어드는데 소요

되는 시간이므로 초기질량 yo 가 절반으로 줄어드는데 소요되는 시간이 5730년이다.

따라서 이를 아래식에 적용하여 비례상수 k를 구할 수 있다.​

이를 이용하여 C14가 당초 보다 20[%]밖에 남아 있지 않으므로 사망연대를 추정할 수

있다. 20 [%]는 1/5이므로 이를 위 수식에 적용하면 다음과 같다.​

#뉴톤 #냉각법칙 #미분방정식 #상수 #적분 #미분 #리비 #탄소연대추정 #방사성 #동위원소 #탄소 #반감기 #비례상수

1. 미분

​

독립변수 x가 연속적으로 변함에 따라 종속변수 y도 연속적으로 변할 때 어느 한 점에서 종속변수 변화량 Δx와 독립변수 변화량 Δy의 비율의 극한을 그 점에서의 ‘미분계수’ 또는 ‘순간변화율’이라고 합니다.

이에 비해 단순히 종속변수 변화량 Δx 와 독립변수 변화량 Δy의 비율을 평균변화율이라 하죠.

​

1-1. 평균변화율

​

x가 a로부터 a+Δx인 b로 변화될 때 함수 f(x)의 평균 변화율은 다음과 같습니다.

​

아래 [그림 1]에서 파랑색 직선의 기울기가 평균변화율을 뜻합니다.

1-2. 순간변화율 (미분계수)

(1)식에서 Δx→0일 때의 극한값이 순간변화율입니다. 수학적으로 표현하면 아래 식과 같습니다.​​

[그림 1]에서 주황색 직선의 기울기가 a인 지점에서의 순간변화율을 뜻합니다.

​

[예제1] 순간변화율​

[풀이] 아래와 같이 미분계수는 1/2이 나옵니다. 한편 풀이에서 빨강색 부분은 같은 양을 나누고 곱해주었음을 뜻합니다.​

[예제2] 도함수

[풀이] 도함수는 아래와 같이 구해집니다.​

한편, x=1에서의 미분계수를 구한고자 한다면 위의 도함수에서 x대신에 1을 대입하면 됩니다.

그러면 (E-1)식과 같이 1/2이 동일하게 구해지는 것을 알 수 있습니다.

결국 도함수를 구해 놓으면 어느 지점에서건 미분계수를 쉽게 구할 수 있게 됩니다.

​

1-4. 상미분

​

위에서 도함수를 구하는 과정을 미분이라고 했는데요. 이때 원래 함수의 독립변수가 하나인 경우 이 함수를 미분하는 것을 상미분이라고 합니다.

통상적인 미분이라는 뜻이에요.

상미분 개념은 예를 들어 어떤 기계장치의 온도가 기계로 들어가는 교류신호의 실효값에만 의존하는 경우 실효전압의 크기가 증가함에 따라 온도가 어떠한 기울기로 증가하는 지를 알고자 할 때 적용할 수 있습니다.

구체적인 예로는 위 [예제2]가 바로 상미분에 해당합니다. 예제에서 x를 교류 실효값의 크기라 생각하고 f(x)를 온도라고 생각하면 됩니다.

​

1-5. 편미분

​

상미분은 변수가 하나인 경우의 미분이라면 편미분은 변수가 2개 이상인 경우의 미분법을 말합니다.

편미분은 하나의 변수에 대해 미분할 때 다른 변수는 상수로 취급합니다.

편미분 개념은 어떤 기계 장치의 온도가 기계로 들어가는 교류 실효값뿐만 아니라 압력에도 의존한다고 생각해봐요. 그러면 실효값과 압력이 달라지면 온도가 달라지는거에요.

이때 압력을 고정하고, 즉 압력을 상수로 취급하고 실효값에 따른 온도의 기울기를 구하는 방법이 편미분입니다. 물론 실효값을 상수로서 고정하고 압력에 따른 온도의 기울기를 구하는 것도 편미분입니다.

편미분의 기호는 다음과 같습니다. 예를 들어 변수가 여러개인 함수 f를 x로 편미분하고자 한다면 아래와 같이 쓰면 됩니다.​

[예제3] 편미분​

이 함수를 x와 y에 관해 각각 편미분하여라.

​

[풀이]

먼저 x에 관해 편미분부터 하면, y를 상수로 취급하면 됩니다.

이때 상수를 미분하면 0이 되는 것을 상기하세요.​

다음에는 y에 관해 편미분하면 x를 상수로 취급하면 됩니다.

2. 미분방정식 (Differential equation)

​미분방정식이란 ‘하나 또는 그 이상의 독립변수에 관하여 하나 또는 그 이상의 종속변수의 도함수 또는 미분을 포함하는 방정식’을 말합니다.

특히 독립변수가 하나인 경우 상미분방정식(상미방, ODE, Ordinary Differential Equation), 두개 이

상인 경우 편미분방정식(편미방, PDE, Partial Differential Equation)이라고 부릅니다.

​

2-1. 상미분방정식

​

상미분방정식의 예시는 다음과 같습니다.​

(6)식을 보시면 y를 x로 미분하는 dy/dx항이 수식에 포함된 것을 볼 수 있어요.

이렇게 주어진 미분방정식을 푼다는 말은 독립변수가 x이고 종속변수가 y인 함수 y=f(x)를 구한다

는 의미로 보시면 됩니다.

​

2-2. 편미분방정식

​

편미분방정식의 예시는 다음과 같습니다.

(7)식을 보시면 u를 t로 편미분, u를 x로 편미분, u를 y로 편미분하는 내용이 포함된 방정식임을 알 수 있어요. 이렇게 주어진 편미분방정식을 푼다는 말은 독립변수가 x, y, t이고 종속변수가 u인

함수 u=f(x,y,t)를 구한다는 의미로 보시면 됩니다.

​

3. 미분방정식 구분

​

미분방정식은 다양한 모양을 가질 수가 있어요. 미분을 2번하는 방정식, 3번하는 방정식도 있을 수 있고 상미분과 편미분으로 구성된 방정식도 있을 수 있어요.

그래서 미분방정식을 구분하기 위한 이름이 있어야 합니다. 이때 사용되는 것이 미분방정식의 ‘계수’와 ‘차수’, ‘선형’과 ‘비선형’입니다.

​

3-1. 계수와 차수, 선형과 비선형

​

계수란 미분방정식에 포함되는 최고계 도함수의 계수를 말합니다.

미분이 한번인 dy/dx는 1계, d2y/dx2 는 2계가 됩니다. 미분방정식에서 주어지는 도함수의 가장

큰 계수를 기준으로 이름이 붙습니다.

또한 차수란 미분방정식에 포함되어 있는 최고계 도함수의 지수를 말합니다.

예를 들어 (y′′′)3 은 지수가 3이므로 3차가 됩니다.

선형 미분방정식은 종속변수와 그 도함수가 1차이고 각 계수가 독립변수에만 의존하는 것을 말합니다.

이에 비해 비선형 미분방정식은 종속변수와 그 도함수가 지수를 갖거나 계수가 종속변수를 포함하거나, 비선형 함수 등을 포함하는 경우를 말합니다.

​

3-2. 미분방정식 구분의 예​

(10)식에서 3계 도함수가 3제곱이므로 3차 미분방정식이 되며, 또한 이 때문에 도함수가 1차가 아니므로 비선형이 됩니다. 차수는 최고계 도함수를 기준으로 결정된다는 것을 기억하세요.​

(12)식에서 종속변수인 u가 제곱(즉, 2차)의 형태여서 1차가 아니므로 비선형 방정식이 됩니다.​

(13)식은 계수 (1−y)가 종속변수를 포함하여 독립변수만으로 구성되어 있지 않으므로 비선형이 됩니다.​

(14)식은 종속변수가 비선형함수로서 1차가 아니므로 비선형이 됩니다.

​

#미분 #방정식 #미분방정식 #편미분 #비선형함수 #선형함수 #독립변수 #종속변수 #계수 #차수

#도함수 #함수 #실효값 #상수 #변화율 #순간변화율 #접선 #기울기

​

1. 미분방정식이란 ?

​

미분방정식이 왜 중요한 걸까 ?

우리가 사는 세상의 모든 물체를 볼 때 물체의 변화(운동, 상태 등)에 관심을 갖기 때문이다.

물체의 변화는 움직임일 수도 있고 얼었다 녹는 상태의 변화일 수도 있고 부피나 모양의

변화일 수 있다. 이처럼 우리는 물체의 변화에 관심을 갖게 되는데 이런 물체의 변화를 나타내는 것이 미분이다.

물체의 변화 중에서 속도를 예를 들어 보자. 물체의 속도에는 3가지가 있다.

▣ 속도가 없거나

▣ 속도가 일정하거나

▣ 속가 변하거나 이 3가지가 있다.

​

그런데 속도는 거리(L)를 시간(t)로 미분한 것(dℓ/dt)인 것이다.

속도를 수식으로 표현하면 미분항 (dℓ/dt)이 들어가는 미분방정식으로 표현하게 된다.

뉴턴의 운동법칙 1,2,3법칙 중에서 제1법칙이 관성의 법칙이다.

관성의 법칙도 등속도를 유지하려는 법칙이므로 속도와 관련되어 미분과 관련이 있다.

뉴턴의 제1법칙은 속도의 특수한 경우인 "0"인 경우를 제외하고 등속도에 관한 법칙이다.

뉴턴의 제1법칙을 식으로 나타내면 속도 v = k(일정)이 되며​

뉴턴의 제2법칙은 가속도에 관한 법칙이다. 이것도 미분방정식에 해당한다.

뉴턴의 가속도의 법칙도 식으로 나타내면 다음과 같다.​

이처럼 가속도도 미분방정식과 관련이 있다.

​

상대성원리도 마찬가지이다. 상대성원리는 물체가 빛의 속도에 가깝게 빠르게 움직일 때

두드러지게 나타나는 현상인데 그중 특수상대성 원리란 등속도에 관한 것이고 일반상대성

원리는 가속도 운동에 관한 것이다. 이 상대성 원리도 속도와 관련된 사항이므로 미분

방정식에 해당하는 것이다.

우리가 관심을 갖고 있는 것들을 식으로 나타내면 이처럼 많은 것들이 미분방정식으로

표현되는 것들이다. 왜냐하면 우리는 변화하는 것들에 대하여 관심이 많기 때문이다.

​

2. 간단한 미분방정식의 예

【 뉴톤 역학 】

① 썰매장에서 몸무게 50[kg]의 아이를 5[Newton]의 힘으로 계속하여 밀면 10초 후에는 아이는 얼마의 속도로 밀려

     나갈까 ? (얼음과의 마찰력은 없다고 가정한다)

 [풀이] 뉴턴의 제2법칙 가속도의 법칙에 의하면 가속도는 다음과 같다.​

여기서 F = 5N, 질량(아이 몸무게) = 50kg 이므로 이를 위식에 대입하면​

v(10) 을 구하기 위해서는 C를 구해야 하는데 C는 초기조건이라고 한다. 조건에서

처음상태는 아이를 밀기 전이므로 즉, 처음에 아이는 정지해 있었으므로 v(0) = 0이다.

위 식에서 시간 t = 0 일 때 속도 v = 0, v(0) = 0 을 만족해야 한다.​

② 위 조건에서 10초 후에는 처음 위치에서 얼마만큼 떨어져 있겠는가 ?

  ▣ 잘못된 풀이 : ℓ = v × t 이므로 ℓ = 1 × 10 = 10 [m] 이다.

  ▣ 올바른 풀이법 : 아이를 밀 때 계속하여 힘을 가해 주므로 가속도 운동을 하게 된다.

처음 밀 때 속도가 "0" 에서 변화를 하므로 위에서 처럼 등속도 운동으로 풀면 안된다.

속도 v(t)는 거리를 시간으로 미분한 것이다.​

거리(ℓ)을 풀기 위해서 양변을 적분을 하면 다음과 같다.​

여기서도 초기조건 C은 정지상태이므로 ℓ(0) = 0 이란 조건을 이용하여 C를 구한다. 

#미분 #적분 #미분방정식 #뉴턴 #관성법칙 #가속도 #운동법칙 #변화율 #접선 #속도