▣ 중거리 송전선로에서는 R, L, C 까지만 다룬다.
⊙ G는 고려하지 않는다.
Z = r + j ω L
Y = G + j ω C 인데 중거리 송전선로에서는
Z = r + j ω L
Y = j ω C 어드미턴스는 용량성 리액턴스만 고려한다.
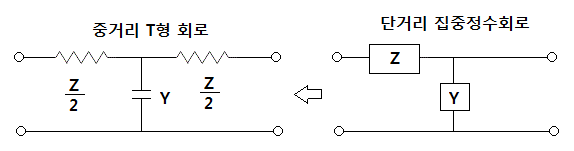
▣ 단거리 송전 선로에서는 집중정수 회로 T형과 π 형이 있다.
그런데 중거리 송전선로에서는 임피던스 Z와 어드미던트 Y를 양분하여
각각 송전단과 수전단에 안분한다.
1. 송전단전압, 송전단 전류 구하기

▣ T형 회로
⊙ 임피던스 Z 는 송수전단 양단에 Z/2 씩 양분하여 집중시키고 어드미던스 Y는 송전선로
중앙에 집중시킨 회로이며 이렇게 하여 궁극적으로 구하고자 하는 것은
송전단 전압과 송전단 전류를 구하고자 한다.
위 식에서 송전단 전압, 전류, 충전전압, 전류를 구해 보자.


위와 같은 방법으로 Es를 구하면 아래와 같이 정리할 수 있다.

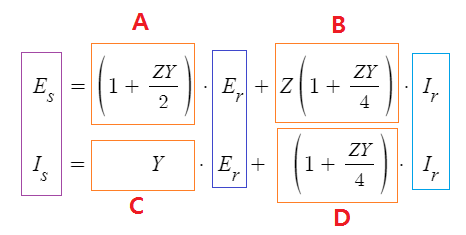
중거리 송전선로에서 송전전압, 전류 이야기가 나오면
먼저 4단자 정수식을 떠 올려야 한다.
Es = A · Er + B · Ir
Is = C · Er + D · Ir
지금까지는 전류 · 전압 관계식으로 풀어 보았다.
[행렬식으로 풀어 보자]

위 그림과 같이 임피던스를 하나의 망으로 싸서 별도로 계산하여 보자
그런데 어드미턴스 Y는 고려하지 않고 임피던스만 행렬식으로 계산하여 보자
위 그림에서 점선으로 싼 부분을 4단자 정수로 나타나면 다음과 같다.

그럼 행렬식을 이용하여 4단자 정수 A, B, C, D 가 무엇을 의미하는지 알아 보자.
먼저 4단자 정수를 행렬식으로 표현해 보자.
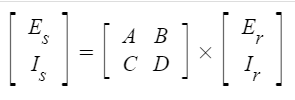
Es = A · Er + B · Ir
Is = C · Er + D · Ir
이제 4단자 정수를 구해 보자.
산술적으로 계산한다고 하면

그러나 이렇게 구하면 실제 구하기도 힘들다.
그러므로 구하기 쉽게 하기 위하여 4단자 정수 A를 구할 때는 B항을 없앤다.
이렇게 하기 위하여 4단자 정수에는 필요한 시험이 있다.
즉, 회로의 4단자 정수를 구하기 위하여 2가지 실험(시험)을 한다.
바로 무부하시험과 단락시험이다.
4단자 정수 - 무부하시험
- 단락시험
무부하 시험을 알아 보자.
무부하 시험은 수전단 측에 부하가 없다는 말이다.
부하가 없으면 전류가 흐르지 않는다.

다음으로 단락시험을 알아 보자. 단락시험은 수전단 측 선로를 단락한다는 말이다.
그러면 수전단측의 전류는 부하(임피던스)가 있는 곳으로 흐르지 않고
단락된 곳으로 전류가 전부 흐른다. 이렇게 되면 부하측 즉 임피던스 측은
전류가 흐르지 않게 되므로 Er = Ir · Z = 0 이 된다.

그러므로 무부하시험은 Ir = 0 이 되며, 단락시험은 Er = 0 으로 놓고
4단자 정수 A, B, C, D를 구한다.
앞으로 무부하라는 말은 Ir = 0 이란 것을, 단락시험은 Er = 0 을 떠올리도록 하자.
[무부하시험, 단락시험을 전제로 4단자 식을 표현해 보자]

4단자 정수를 구한 후에 검산하는 방법이 있다.
검산하는 방법은 다음과 같다.
" A D - B C = 1 " 이다.
Es = A · Er + B · Ir
Is = C · Er + D · Ir
4단자 정수 A, B, C, D는 무엇과 무엇의 관계인지 아래 그림으로 알아보자.


[먼저 임피던스 Z만 있는 회로에서 4단자 정수를 구해보자]

왼쪽그림은 Z만 있는 회로이고 오른쪽 그림은 어드미턴스 Y만 있는 회로이다.
A를 구해 보면

B를 구해 보자.
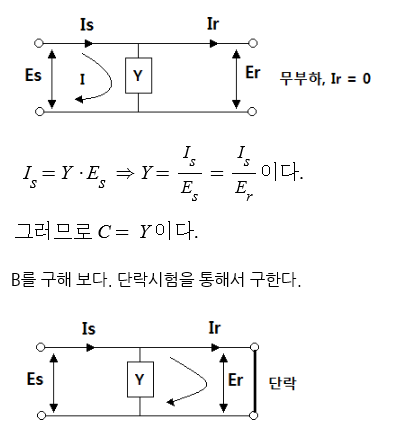
부하측이 단락된 회로에서 전류 I 를 구해 보자.

[2번째 Y만의 회로에서 4단자 정수를 구해보자]
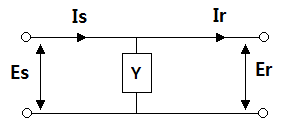
Es = A · Er + B · Ir
Is = C · Er + D · Ir

① 먼저 A를 구해 보면
위 그림의 회로에서 송전단과 수전단 측에서 바라 본 Y 측의 전압은 같으므로
A = Es / Er = 1 이다.
C를 구해 보면 무부하 상태이므로 전류 I는 송전단과 어드미턴스 측으로만 흐른다.
B는 임피던스를 의미하므로 단락된 상태에서는 임피던스가 없으므로 "O" 이 된다.
D를 구해 보자.
위 그림에서 단락된 상태에서 Is = Ir 이므로 Is / Ir 은 "1" 이므로 D는 "1"이 된다.
검산해 보자.
AD (1×1) - BC (Y×0) = 1 이다. 맞다.
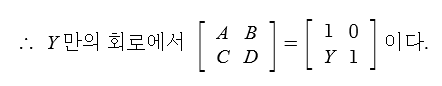
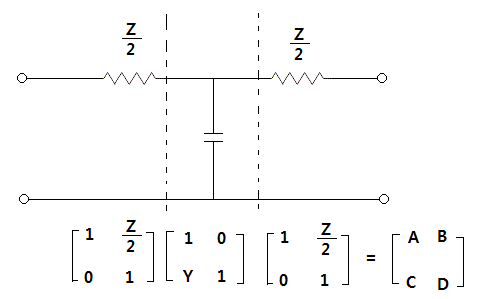
이제 T형 회로의 4단자 정수를 알아 보자.
T의 임피던스와 어드미턴스를 각각 나누어 4단자 정수를 구한 후에
이들 4단자 정수를 행렬식을 이용하여 계산한다.

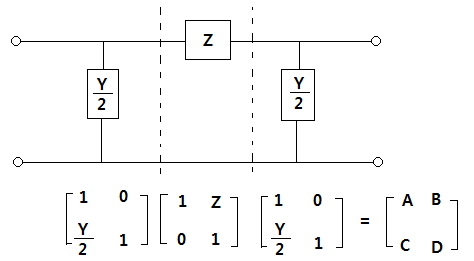
이제 π형 회로의 4단자 정수를 알아 보자.
π형 회로에서도 임피던스와 어드미턴스를 각각 나누어 4단자 정수를 구하고
구한 4단자 정수를 다시 행렬식을 이용하여 합산한다.

이상 중거리 송전선로에서 4단자 정수를 이용하여
송전전압과 송전전류를 구하는 식에 대하여 알아 보았다.
내용이 길다 보니 중거리 송전선로에서 4단자 정수를 구하는 목적인
송전전압과 송전전류를 구하는 목적을 잊곤한다.
'전기인이 되는 길 > 전력공학' 카테고리의 다른 글
| 조상설비 - 역률 : 전력공학 (0) | 2021.09.01 |
|---|---|
| 중거리 송전선로 관련 문제 풀이 (0) | 2021.09.01 |
| 전압관계식 및 경제적인 송전전압, 송전전력과 송전전압 관련 기출문제 (0) | 2021.08.31 |
| 송전단 전압과 전압강하 근사식, 송전전압과 송전전력의 관계 (전력손실) (0) | 2021.08.31 |
| 송전선에서 복도체 방식의 특징 (0) | 2021.08.31 |
