1. 2단자망
▣ 2단자망은 어떤 회로가 주어졌을 때 이 회로의 구성을 알아내기 위해 2개의 단자를
빼어내 전압, 전류를 인가하여 회로의 구성을 알아 보고자 하는 것이다.
가. 정의 : 임의의 선형회로망에서 외부로 나온 단자가 2개인 회로망
▣ 능동회로망 : 회로망 내부에 기전력이 있는 회로망
▣ 수동회로망 : 회로망 내부에 기전력이 없는 회로망
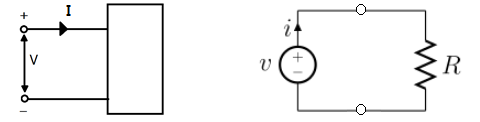
나. 구동점 임피던스
▣ 회로에 기전력이 인가되었을 때 전원 측에서 바라 본 임피던스 값

⊙ 이 때 전원이 교류가 입력되었을 경우 회로분석에 있어서 주파수의 영향이 크게 되는데
교류가 인가되면 임피던스는 주파수의 영향을 받게 되고 주파수는 jω인데 이를 그대로
반영하면 계산이 복잡해진다. 따라서 계산을 단순화하기 위해 "jω = s"로 단순화하여
2단자망을 분석한다.
▣ 2단자망은 입력측에서 분석할 수도 있고 출력측에서도 분석할 수 있는데 입력 측, 전원
측에서 회로의 임피던스를 분석하는 것을 "구동점 임피던스"라고 한다.

▣ 임피던스 구성을 알아 보자.
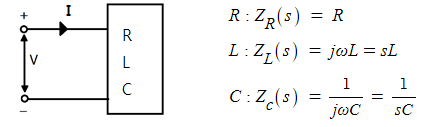
▣ 계산을 편리하기 위해 jω = s 로 치환하면, 저항 R 은 주파수와 관계 없으므로 그대로 R
이고 유도성 리액턴스 jωL = sL 로 용량성 리액턴스 1/jωC =1/sC 로 표현할 수 있다.
예1) 다음 회로의 구동점 임피던스를 구해 보자.
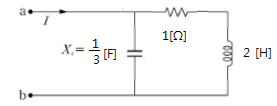
▣ jω = s 로 변환하여 구동점 임피던스를 구해 보자
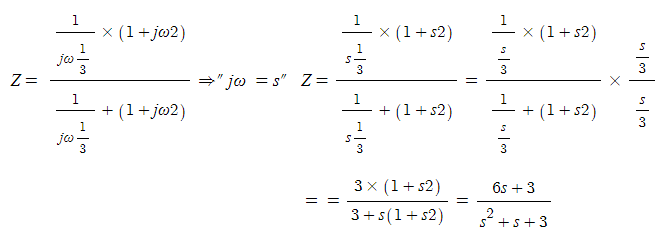
예2) 그림 회로의 구동점 임피던스를 구해 보자.
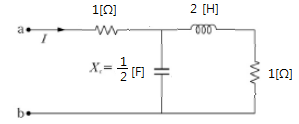
▣ jω = s 로 변환하여 구동점 임피던스를 구해 보자.
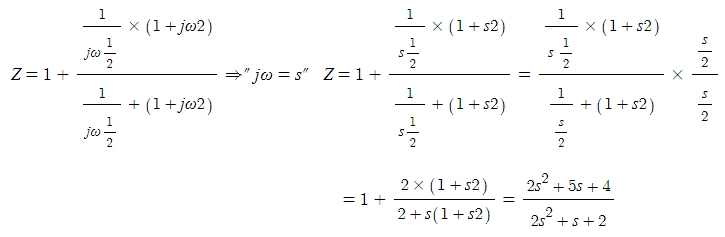
다. 임피던스의 일반화
▣ jω = s 로 변환한 임피던스 구성의 일반화식을 기억하고 s로 표시된 임피던스 식을
R-L-C 회로 그려낼 수 있도록 한다.
① R - L - C 직렬회로
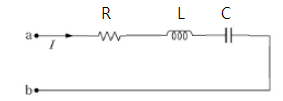
▣ R-L-C 직렬회로의 구동점 임피던스의 일반화식은 다음과 같다.
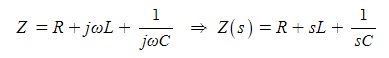
② R - L - C 병렬회로
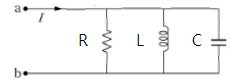
▣ R-L-C 병렬회로의 구동점 임피던스의 일반화식은 다음과 같다.
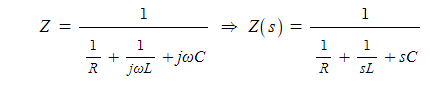
예1) 임피던스 Z(s) = (5s+2) / s 로 표시되는 2단자 회로의 구성은 ?
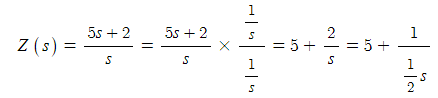
※ 회로의 구성 : 분자의 차수를 분모차수 보다 낮춘다. 분자 차수가 분모 차수 보다 낮춘다
는 것은 S로 분자 분모를 나누어 준다는 의미이다.
위 식을 일반화식과 비교하여 보면 R 과 C로 구성된 회로임을 알 수 있다.
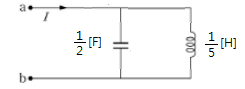
즉 위 식은 다음과 같은 회로를 나타낸다.
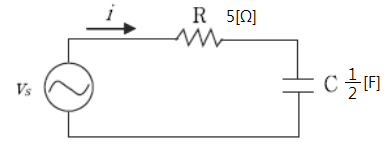
예2) 임피던스 Z(s) = 2s / (S2 + 10) 로 표시되는 2단자 회로를 구성하라.
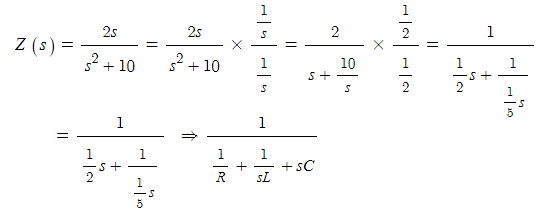
※ 분모차수가 분자보다 작은 경우에는 분자를 "1" 로 만들고 분모의 분자를 "1"로
만들어 준다. 1/s 꼴로 바꾸어 준다.
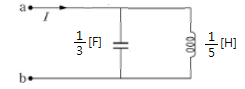
예 3) 임피던스 Z(s) = 3s / (S2 + 15) 로 표시되는 2단자 회로를 구성하라.

라. 영점과 극점
▣ 임피던스가 다음 식으로 표현될 때 영점과 극점에 대하여 알아 보자.
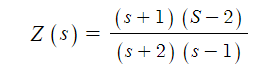
① 영점 : 회로망 함수 Z(s)가 "0"이 되는 S의 값, 즉 "분자 = 0" 인 경우를 말한다.
위 식에서는 S = -1, 또는 S = 2 일 때 영점이라고 한다.
◈ 영점은 회로가 단락인 상태를 말한다. 즉, 임피던스가 "0"인 경우는 단락상태를
의미하기 때문이다.
② 극점 : 회로망 함수 Z(s)가 "∞" 가 되는 S의 값. 즉 "분모 = 0"이 되는 상태를 말한다.
◈ 극점은 회로가 개방상태를 말한다. 즉, 임피던스가 "∞"가 되는 경우에는 회로가
개방된 경우를 의미하기 때문이다.
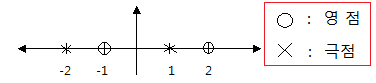
※ 영점과 극점의 좌표상 표시방법은 영점은 "O", 극점은 "X"로 표시한다.
2. 정저항 회로
▣ 정저항 회로는 순수한 저항만 있는 회로와 같은 상태의 교류회로를 말한다. 교류회로는
주파수가 영향을 미치게 되는데 L-C가 공진상태를 이루어 주파수가 임피던스로 작용하
지 않는 회로를 말한다.
▣ 정저항 회로는 다음의 2 종류의 회로를 기억해 두자.

▣ 다음 회로를 이용하여 정저항 회로의 조건을 유도해 보자.
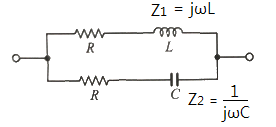
◈ 정저항 회로 조건 Z = R의 조건을 이용하여 유도해 보자.
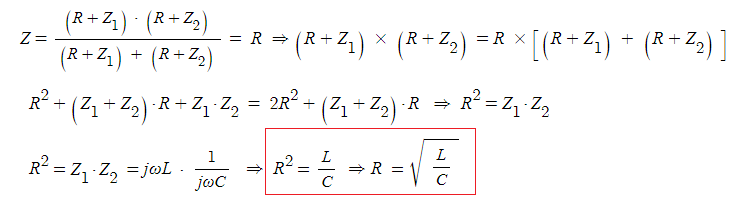
3. 역 회로
▣ 역회로는 쌍대관계에 있는 소자로 회로를 구성하는 것으로 두 임피던스의 곱이 특정상
수의 제곱값을 나타낼 때 두 회로는 역회로 관계에 있다고 한다.
※ 쌍대 관계
◈ 직렬 ⇔ 병렬, L (리액터) ⇔ C (콘덴서)

▣ Z1·Z2 = K2 일 때 Z1과 Z2 는 K에 관하여 역회로 관계에 있다고 한다.
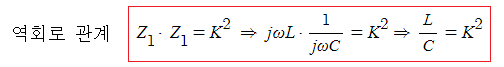
▣ 회로(직렬, 병렬)와 연계하여 역회로를 알아 보자.
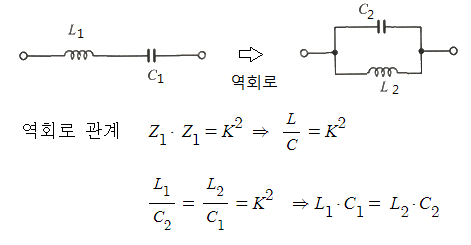
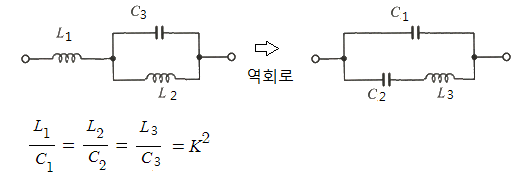
예) 다음 회로의 역회로를 구하라.
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 4단자 정수 - 4단자 전송 파라미터 (0) | 2022.01.16 |
|---|---|
| 2단자망 - 임피던스 함수, 정저항 · 역회로 기출문제 풀이 (0) | 2022.01.15 |
| 비정현파 교류 전력 (0) | 2022.01.11 |
| 비정현파 교류 (0) | 2022.01.11 |
| 대칭좌표법, 고장계산 기출문제 풀이 (3) | 2022.01.10 |
