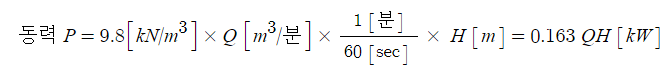아낌없이 주는 나무

1. 방사압력이 0.3[MPa]인 유체가 노즐을 통해 방사되고 있다. 유속 [m/s]을 구하시오.  [8점] ★★★★★​

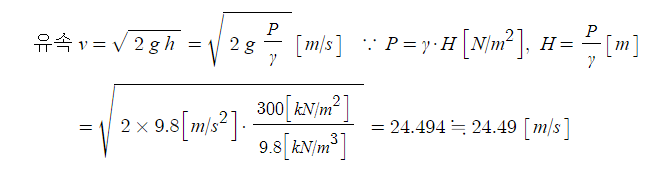
[해설] 유속

▣ 토리첼리 정리​

여기서, v : 유속 [m/s]

            g : 중력 가속도 (9.8 [m/s2])

            H : 높이 [m]

             P : 압력 [kPa = kN/㎡]

             γ : 물의 비중량 (9.8 [kN/㎥]

⊙ 압력 P : 0.3[MPa] = 300[kPa] =300 [kN/㎡]​

2. 지상 30[m]의 창문으로 부터 구조대응 로프의 모래주머니를 자연낙하시켰을 때 지상에 도착할 때의 속도는 몇 [m/s]인

    가 ? [4점] ★★★

[풀이]​

[해설] 유속

▣ 토리첼리의 정리​

여기서, v : 유속 [m/s]

             g : 중력 가속도 (9.8 [m/s2])

             H : 높이 [m]

              P : 압력 [kPa = kN/㎡]

              γ : 물의 비중량 (9.8 [kN/㎥]

    ⊙ 높이 H : 30 [m]​

3. 길이 600[m]인 관로 속을 2.5[m/s]의 속도로 물이 흐르고 있다. 출구의 밸브를 1.3초 후에 잠그면 압력 상승 [kPa]은 얼마

     인가 ? (단, 수관속의 유속 a = 1,000 [m/s]이다)  [4점] ★★★

[풀이]​

여기서, △P : 상승압력 [kPa]

             α : 배관속의 유속 [m/s]

             v : 유속 [m/s]

            g : 중력가속도 (9.8 [m/s])

4. 내경이 25 [㎜]인 급수배관에 정상류가 180 [ℓ/min] 으로 흐를 때 속도수두 [m]는 얼마인가 ? (단, 중력가속도는 9.8[m/s]

    이다.) [3점] ★★★★★​

[해설]

가. 토리첼리의 정리​

여기서, v : 유속 [m/s]

            g : 중력가속도 (9.8 [m/s2])

            H : 높이 (속도수두)[m])

            γ : 물의 비중량 (9.8 [kN/㎥])

            P : 압력 [Pa = N/㎡]

나. 유량​

여기서, Q : 유량 [㎥/s]

              A : 배관의 단면적 [㎡] = π/4 · d2 [㎡]

              v : 유속 [m/s]

              d : 내경 [m]

5. 소화용수를 어떤 고층건물 옥상에서 쏟아 부었다. 소화용수가 떨어진 뒤 3초가 지날 때의 낙하속도는 얼마인가 ?

  ▣ 중력가속도 = 속도 / 시간, 속도 = 중력가속도 × 시간​

[해설] 낙하 속도

   중력가속도 = 속도 / 시간 , g = v / t, v = g · t [m/s]

   여기서, v : 낙하속도 [m/s]

                g : 중력가속도 (9.8 [m/s2])

                t : 시간 [s]

6. 다음 그림과 조건을 참조하여 개방된 고가수조에서 배관을 통하여 물을 방수할 때 ② 지점에서의 방출압력 [kPa]을 구하

    시오. [5점] ★★★

  ⊙ 대기는 표준대기압 상태이다.

  ⊙ 배관의 안지름은 100 [㎜] 이다.

  ⊙ 배관의 길이는 250 [m] 이다.

  ⊙ 방출유량은 2,500 [ℓ/min]이다.

  ⊙ 총 마찰손실수두는 7 [m] 이다.

  ⊙ 방출압력을 구할 때 계기압력으로 구한다.

[풀이] 베르누이의 연속방정식으로 풀어 보면​

위 식에서 수조의 표준대기압 = "0", 수조의 유속 = "0"을 대입하면​

[참고] 적정소방수류가 도달된 최대 높이​

여기서, V : 적정 소방수류가 도달한 최대 높이 [m]

             H : 건물로 부터 소화노즐까지의 거리 [m]

             Q : 유량 [ℓ/s]

  ⊙ H (건물로 부터 소화노즐까지의 거리) : 15 [m]

  ⊙ Q (유량) : 1,000 [ℓ/min] × 1/60​

7. 안지름이 155[㎜]인 관으로 1시간 30분 동안 60 [ton]의 물을 350 [m] 떨어진 곳으로 송수할 때 가하여야 할 필요한 압력

    [kPa]을 구하시오. (단, 마찰손실계수는 0.03이다.) [5점] ★★★★★

※ 달시-웨버의 식을 이용​

[ 압력 환산]

1[atm] = 760 [㎜Hg]

           = 0.101325 [MPa]

           = 101.325 [kPa]

           = 101,325 [Pa]

           = 10.332 [mAq = mH2O]

           = 10,332 [㎜Aq = ㎜H2O]

            = 1,013 [bar]

8. 수평으로 된 어느 소방배관의 레이놀즈수가 1,000으로 유체가 흐르고 있다. 유량이 200 [ℓ/min], 배관의 길이 100[m],

    관지름이 40 [㎜] 일 때 다음을 구하시오. [4점]  ★★★★★

 가. 배관의 마찰손실 수두 [m]를 구하시오. (단, 달시 - 웨버의 식을 이용하여 구할 것)

 나. 출발점의 압력이 0.8[MPa]이라면 끝지점의 압력 [MPa]을 구하시오. (단, 소수점 여섯째 자리까지 구하시오.)

[풀이]

 가. 배관의 마찰손실 수두 [m]를 구하시오. (단, 달시 - 웨버의 식을 이용하여 구할 것)

    ※ 달시-웨버의 식은 마찰손실계수, 관의 길이, 속도와 관경에 의한 손실수두를 구하는 식이다.

나. 출발점의 압력이 0.8[MPa]이라면 끝지점의 압력 [MPa]을 구하시오. (단, 소수점 여섯째 자리까지 구하시오.)

※ 관로 등의 입 · 출구의 한쪽의 에너지가 주어지고 다른 쪽의 에너지를 물어 보는 문제는 베르누이의 연속방정식으로

    풀이를 한다.​

⊙ 위 식에서 수평배관이므로 위치수두와 관경 및 유량(유속)이 입구와 출구가 같으므로 속도수두와 위치수두가 입 · 출구

     에서 같게 되어 다음과 같이 수식을 변경할 수 있다.​

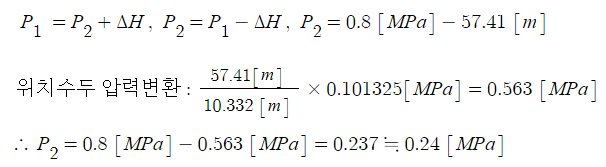
9. 수평으로 곧게 설치되어 있는 40[m] 길이의 배관내에 유량 300 [ℓ/min]의 물이 흐르고 있다. 배관 말단의 수압 [MPa]을

    구하시오. (단, 배관인입측의 수압게는 0.4[MPa] 을 가리키고 있으며, 구경 40 [㎜] 강관의 1 [m]당 마찰손실에 의한 압력

    강하는  △P = 1.08 × 10-7 × Q1.85 이며 Q는 유량 [ℓ/min]이다.)

[풀이]

  △P = 1.08 × 10-7 × Q1.85 × 40 [m] = 0.165 [MPa]

  ∴ 배관 끝 부분의 압력 = 입구측 압력 - 마찰손실 압력  = 0.4[MPa]-0.165 [MPa] ≒ 0.24 [MPa]

[해설] 배관 끝 부분의 압력 = 배관 입구측 압력 - 마찰손실 압력

   ⊙ 배관 입구 부분의 압력 : 0.4 [MPa]

   ⊙ 마찰손실 압력 : 문제의 단서에서 1 [m] 당 마찰손실에 의한 압력강하는

     △P = 1.08 × 10-7 × Q1.85 이라고 했으므로

     △P = 1.08 × 10-7 × Q1.85 × 40 [m] = 0.165 [MPa]

​

10. 어느소화배관내에 3 [m/s]의 유속으로 소화수가 흐르고있다. 마찰손실계수가 0.016, 배관길이가 1.000[m], 배관내경이

      100[m]일 때 배관의 조도를 구하시오. (단, 배관 마찰손실은 달시-웨버공식과 하젠 - 윌리엄스 공식을 이용하고 ,답은

      정수로 쓰시오.) [5점] ★★★★

[풀이] 조도(C)를 구하는 식은 하젠-윌리엄스식 밖에 없다.​

그런데 위식에서 조도(C)를 구할려면 압력변화와 유량을 구해야 한다. 압력변화를 알기 위해 달시-웨버식을 사용하게

 된다.

① 압력변화를 달시 - 웨버의 식으로 알아 보자.​

② 체적유량식을 이용하여 유량을 구해 보자.

     Q = A · v = π/4 · d2[㎡] × v [m/s] = π/4 × 0.12 × 3 × 60 = 1,380 [ℓ/min]

③ 하젠 - 윌리엄스식으로 조도(C)를 구해 보자.

11. 어느 수계 소화설비 배관 (일정한 관경)의 두 지점에서 압력계로 흐르는 물의 수압을 측정하였더니 각각 0.45 [MPa],

      0.4[MPa]이었다. 만약, 이 때의 유량 보다 1.5배 유량을 흘러 보냈다면 두 지점간의 수압차 [MPa]를 구하시오.

      (단, 배관의 마찰손실은 하젠 - 위리엄스 공식을 이용한다) [4점] ★★★★★

[풀이] ​

위식에서 상수 C, D, L은 같으므로 아래식으로 위식을 나누면 다음과 같다.​

[해설] 두 지점간의 수압차 : 하젠 - 윌리엄스 공식​

위 하젠 - 윌리엄스 식에서 압력변화는 유량에 비례하므로​

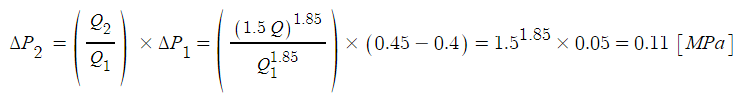
12. 직경 400[㎝]인 소화배관에 0.04[㎥/s]의 유량이 흐르고 있다가 ①, ②의 분기관으로 흐르다 다시 합쳐져 있다. 각 분기

      관에서의 관 마찰계수는 0.022라 할 때 ①,②의 유량 [㎥/s]을 계산하시오. (단, Darsy-Weisbach 식을 이용한다) [6점]

      ★★★★★

※ 최근 자주 출제

 ※ 병렬관로

  Q = Q1 + Q2

      = A1 · v1 + A2 · v2

  ※ Q1, Q2의 마찰손실수두는 동일하다.

  ※ 문제에서 제시한 조건에 따라 달시-바이스바흐식과 하젠-윌리엄스식을 적용한다.

[풀이] 달시 - 웨버식​​

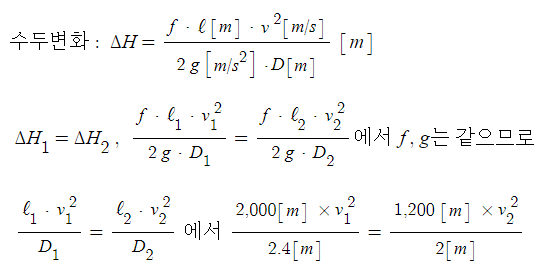
위 식을 속도 v에 대하여 정리를 하면

위에서 산출한 값을 체적유량 공식에 대입을 하면​

13. 다음 그림은 어느 배관 평면도이며, 화살표 방향으로 물이 흐르고 있다. 배관 ABCD 및 AEFD 간을 흐르는 유량 [ℓ/min]

     을 각각 계산하시오. (단, 주어진 조건을 참조하시오)  [8점] ★★★★★

[조건]

① 하젠-윌리엄스의 공식은 다음과 같다.​

(단, △P : 배관의 길이 1[m]당 마찰손실압력 [MPa],

       Q : 유량 [ℓ/min], D : 관의 안지름 [㎜] )

  ② 호칭 50[㎜] 배관의 안지름은 54 [㎜] 이다.

  ③ 호칭 50 [㎜] 엘보 (90˚)의 등가길이는 1.6 [m]이다.

  ④ A 및 D점에 있는 티(Tee)의 마찰손실은 무시한다.

  ⑤ 루프(Loop) 배관 BCFEB의 호칭구경은 50 [㎜] 이다.

[풀이] L1 (ABCD) : 8 +10 + 6 + (1.6 ×2) = 27.2 [m]

          L1 (AEFD) : 2 +10 + 4 + (1.6 ×2) = 19.2 [m]

※ 마찰손실압력 △P(ABCD) = △P(AEFD) 이므로​

여기서, △P : 마찰압력손실 [MPa]

             Q : 유량 [ℓ/min]

             C : 관의 조도 [100]

             D : 관의 내경 [㎜]

             L : 등가길이 [m]

  ※ 등가길이를 적용할 것

   ① 배관 AECD 유량

     ▣ 병렬관로에서 문제 그림의 관로상 ABCD 방향과 AEFD 방향의 배관마찰손실은 같다.

         ∴ △P (ABCD) = △ P (AEFD)​​

         상수, C(100), D는 동일하므로 양변을 이들 수로 양분을 하면

         L1 · Q12 = L2 · Q22 이 된다.

  ⊙ L1(ABCD) = 8 + 10 + 6 + (1.6 × 엘보 2개) = 27.2 [m]

  ⊙ L2(AEFD) = 2 + 10 + 4 + (1.6 × 엘보 2개) = 19.2 [m]​

② 배관 AEFD의 유량

    Q = Q1 + Q2 에서 Q1 = Q - Q2 이므로

    Q1 = 500 [ℓ/min] - 271.74 [ℓ/min] = 228.26 [ℓ/min]

​

14. 다음 그림과 같은 어느 배관에서 화살표 방향으로 물이 흐르고 있다. 주어진 조건을 참고하여 Q1과 Q2 의 유량을 각각

       구하시오. [8점] ★★★★★

[조건] ① 하젠 - 윌리엄스의 공식은 다음과 같다.​

여기서, △P : 마찰압력손실 [MPa/m]

             Q : 유량 [ℓ/min]

             C : 관의 조도

             D : 관의 내경 [㎜]

             L : 등가길이 [m

  ② 호칭 25 [㎜] 배관의 안지름은 27 [㎜]이다.

  ③ 호칭 25 [㎜] 엘보 (90˚)의 등가길이는 1 [m] 이다.

  ④ 배관은 아연도금 강관을 사용한다.

  ⑤ ⓐ점, ⓑ점에 있는 티(Tee)의 마찰손실은 무시한다.

  ⑥ 배관내에 흐르는 유량은 200 [ℓ/min]이다.

  ⑦ 배관의 각 구간의 길이는 다음과 같다.

     ⓐ - ① : 3 [m] , ① - ② : 10 [m] , ② - ⓑ : 2 [m]

     ⓐ - ③ : 6 [m] , ③ - ④ : 10 [m] , ④ - ⓑ : 7 [m]

​

  가. 배관의 구간 (ⓐ-①-②-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

  나. 배관의 구간 (ⓐ-③-④-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

    [풀이]

 가. 배관의 구간 (ⓐ-①-②-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

   L1 (ⓐ,①,②,ⓑ) : 3 + 10 + 2 + (1×2) = 17 [m]

   L2 (ⓐ,③,④,ⓑ) : 6 + 10 + 7 + (1×2) = 25 [m]​

나. 배관의 구간 (ⓐ-③-④-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

     Q2 = Q - Q1 = 200 [ℓ/min] - 110.44 [ℓ/min] = 89.56 [ℓ/min]

​

[해설]

가. 전체 배관 유량

    Q = Q1 + Q 2

     여기서, Q : 전체 관로 유량

                  Q1 : 병렬관로 유량

                  Q2 : 병렬관로 유량

나. 하젠 - 윌리엄스식​

여기서, △P : 마찰압력손실 [MPa]

             Q : 유량 [ℓ/min]

             C : 관의 조도

             D : 관의 내경 [㎜]

             L : 등가길이 [m]

   ※ 등가길이를 적용할 것

    ① 배관 ⓐ①②ⓑ 유량

      ▣ 병렬관로에서 문제의 관로상 ⓐ①②ⓑ 방향과 ⓐ③④ⓑ 방향의 배관마찰손실은 같다.

        ∴ △P (ⓐ①②ⓑ) = △ P (ⓐ③④ⓑ)​​

상수, C, D는 동일하므로 양변을 이들 수로 양분을 하면

          L1 · Q11.85 = L2 · Q21.85 이 된다.

  ⊙ L1(ⓐ①②ⓑ) = 3 + 10 + 2 + (1 × 엘보 2개) = 17 [m]

  ⊙ L2(ⓐ③④ⓑ) = 6 + 10 + 7 + (1 × 엘보 2개) = 25 [m]​

 ② 배관 ⓐ③④ⓑ의 유량

    Q = Q1 + Q2 에서 Q2 = Q - Q1 이므로

    Q2 = 200 [ℓ/min] - 110.44 [ℓ/min] = 89.56 [ℓ/min]

​

15. 다음 그림과 같은 배관을 통하여 흐르고 있는 유량이 80[ℓ/s]이다. B,C관의 마찰손실 수두는 4[m]이고 B관의 유량은 20

      [ℓ/s]일 때 C관의 내경 [㎜]를 구하시오.  (단, 하젠-윌리엄스의 공식은​

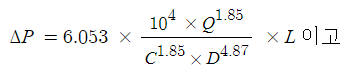
   △P는 압력차 [MPa], L은 배관의 길이 [m], Q는 유량 [ℓ/min], C(조도계수)는 120, D는 내경 [㎜] 이다. [6점] ★★★★

[풀이] C관의 유량 : 80 [ℓ/s] - 20 [ℓ/s] = 60 [ℓ/s] × 60 [s] = 3,600 [ℓ/min]

          마찰손실수두의 압력변환​

#레이놀즈 #베르누이 #달시웨버 #하젠윌리엄스 #압력수두 #에너지보존법칙 #연속방정식 #중력가속도 #속도계수 #유량계수 #속도수두 #위치에너지 #표준대기압 #마찰손실계수 #병렬관로 #표준대기압 #압력수두

1. 베르누이 정리​

여기서, H : 전수두 [m]

             P1, P2 : 압력 [Pa = N/㎡]

             γ : 물의 비중량 (9,800 [N/㎥] = 9.8 [kN/㎥] = 0.0098 [MN/㎥]

             v1, v2 : 속도 [m/s]

             g : 중력가속도 (9.8 [m/s2]

             Z1, Z2 : 위치 수두 [m]

​

2. 토리첼리의 정리

  ▣ 토리첼리의 정리는 위 베르누이의 정리에서 속도수두에 관한 사항이다.​

여기서, v : 유속 [m/sec]

            g : 중력가속도 (9.8 [m/s2]

           H : 높이 [m]

           γ : 물의 비중량 (9,800 [N/㎥])

           ρ : 물의 밀도 (1,000[㎏/㎥])

           P : 압력 [Pa = N/㎡]

​

3. 관의 상당길이 = 등가길이 = 직관장

  ▣ 관의 부속 등의 마찰손실을 동일 구경의 배관의 길이로 환산한 값​

여기서, H : 마찰손실수두 [m]

              f : 마찰손실계수

              ℓ : 배관의 길이 [m]

              v : 유속 [m/s]

              g : 중력가속도 (9.8 [m/s2])

              D : 배관의 직경 [m]

​

5. 하젠-윌리엄스의 식

  ▣ 하젠-윌리엄스의 공식은 관의 마찰압력 손실수두와 조도(관의 거칠기), 관의 직경, 유량 등과의 관계를 나타낸 식이다.​

여기서, △P : 마찰손실압력 [MPa]

              C : 조도 (거칠기)

              D : 배관의 내경 [㎜]

              Q : 유량 [ℓ/min]

              L : 배관의 길이 [m]

   ※ 10^7 이면 마찰손실 압력의 단위는 [kPa]이 된다.

​

6. 병렬관로

▣ 베르누이의 정리에 따라 배관의 입구 부분에서의 에너지는 어떠한 경로로 흘러 가더라도 배관의 출구 부분에 전달되며

     실제 유체 이므로 손실되는 에너지 또한 동일하게 볼 수 있다. (경로가 다르더라도 출발점의 유체의 총에너지와 도착점

      의 유체의 총에너지는 같으므로 경로가 다르더라도 에너지 손실량은 같다) 따라서, 각 병렬관로에서의 마찰손실은 경

      로와 관계없이 동일하다. (△P1 = △P2)

   Q = Q1 + Q2

  여기서, Q : 유량 [㎥/s]

               Q1 : 병렬관로 1에서의 유량 [㎥/s]

               Q2 : 병렬관로 2에서의 유량 [㎥/s]

  ※ 하젠-윌리엄스의 식으로 구하라고 하지 않으면 달시-웨버의 식으로 구한다.

       기본이 달시-웨버의 식이다.

​

7. 노즐의 플랜지 볼트에 작용하는 힘 (반발력)

 ① 플랜지 볼트에 작용하는 힘 

 여기서, F : 플랜지볼트에 작용하는 힘 [N]

              γ : 물의 비중량 (9,800 [N/㎥])

              Q : 유량 [㎥/s]

              A1 : 소방호스의 단면적 ((πd2)/4 [㎡])

              A2 : 노즐의 단면적 ((πd2)/4 [㎡])

              g : 중력가속도 (9.8 [m/s2])

​

 ② 노즐에 걸리는 반발력 (운동량에 따른 반발력)​

 여기서, F : 노즐에 걸리는 반발력 (운동량에 따른 반발력[N])

              ρ : 물의 밀도 (1,000 [N·s2/m4])

              Q : 유량 [㎥/s]

              v1 : 소방호스의 유속 [m/s]

              v2 : 노즐의 유속 [m/s]

​

 ③ 노즐을 수평으로 유지하기 위한 힘​

여기서, F : 노즐을 수평으로 유지하기 위한 힘 [N]

             ρ : 물의 밀도 (1,000 [N·s2/m4])

             Q : 유량 [㎥/s]

             v2 : 노즐의 유속 [m/s]

​

 ④ 노즐에 작용하는 반동력​

  여기서, R : 노즐에 작용하는 반동력 [N]

               P : 방수압력 [MPa]

               D : 노즐 구경 [m]

​

 ※ 플랜지에 작용하는 힘 (계산기에 안들어 가는 경우 해결방안)​

 ※ 1번 공식 다른 방법​

8. 펌프의 분류

 ▣ 원심펌프의 종류 (소방에서는 원심펌프만 사용)

   ① 볼류트 펌프 : 안내깃이 없다. 저가, 저양정 고유량, P↓, Q↑

   ② 터빈펌프 : 안내깃이 있다. 고가, 고양정 저유량, P↑, Q↓

​

9. 펌프의 직렬 및 병렬 운전

   ▣ 펌프를 직렬운전하면 양정이 커지고 토출량은 그대로 이다.

   ▣ 펌프를 병렬운전하면 양정은 그대로이고 토출량은 늘어난다.

​

10. 실제흡입수두 (NPSH)

 ① 유효흡입수두 (NPSHav ⇒ NPSH available)

   ⊙ 펌프설비에서 얻어지는 이용 가능한 유효흡입양정 (펌핑 안해도 사용할 수 있는 수두)​

  여기서, NPSHav : 유효흡입수두 [m]

               Ha : 대기압의 환산수두 [m]

               Hf : 마찰손실의 환산수두 [m]

               Hv : 포화증기압의 환산수두 [m]

               Hh : 낙차의 환산수두 [m] (부압 : -, 정압 : +)

 ② 필요흡입수두 [NPSHre] : 펌프에서 임펠러 입구까지 유입된 물은 임펠러에서 가압되기 직전에 압력강하가 발생한다.

                                               이 때 해당하는 수두가 필요흡입수두[NPSHre]이다.

    ㉠ 펌프제작시 결정되는 고유값으로 설계에 의해 변하지 않는다.

    ㉡ NPSHre 가 클수록 펌프의 흡입능력은 떨어진다.

    ㉢ NPSHre 의 크기는 펌프의 토출량 증가에 따라 커진다. 따라서, 설계시 최대 운전점인 150 [%] 토출량을 적용한다.

  ※ NPSH 계산시 주의할 점

   ⊙ 마찰손실수두 : 정격토출량의 150 [%]를 적용 (최대 운전상태를 적용)

   ⊙ 필요흡입수두(NPSHre) : 비속도 계산시 150 [%] 토출량의 회전수, 유량 및 양정을 적용 (최대 운전상태의 펌프 진공도

                                                를 산출)

​ ③ 공동현상 발생한계 조건

   ㉠ 발생한계 : NPSHav = NPSHre

   ㉡ 발생안함 : NPSHav > NPSHre

   ㉢ 펌프설계시 : NPSHav ≥ NPSHre

11. 동력공식

  ① 동력 P = γ · Q · H 에서 Q의 단위 [㎥/s]

  ② 동력 P = 0.163 Q · H 에서 Q의 단위 [㎥/min]

    ※ 물의 비중량 γ = 9.8 [kN/㎥], 유량 Q [㎥/min]을 대입하면​

    ㉠ 1 [hp] : 0.746 [kW]

    ㉡ 1[ps] : 0.735 [kW]

   ※ 전효율 = 수력효율 × 체적효율 × 기계효율

​

12. 펌프의 동력​

   여기서, P : 동력 [kW], H : 전양정 [m], Q : 유량 [㎥/min], η : 효율, k : 전달계수

      ④ 팬의 동력

  여기서, P : 동력 [kW]

              PT : 전압 [㎜Aq=㎜H2O]

              Q : 풍량 [㎥/min], [1㎥/min × 1 [min] / 60 [sec]]

              η : 전효율

              k : 전달계수

​

13. 상사법칙

 ① 유량 : 펌프의 유량은 회전수에 비례하고 관경의 세제곱에 비례한다.​

  여기서, Q1 : 변경 전 유량 [ℓ/min],           Q2 : 변경 후 유량 [ℓ/min]

              N1 : 변경 전 회전수 [rpm],          N2 : 변경 후 회전수 [ℓ/rpm]

              D1 : 변경 전 관경 [㎜],                D2 : 변경 후 관경 [[㎜]

​

 ② 양정 : 펌프의 양정은 회전수 및 관경의 제곱에 비례한다.​

  여기서, H1 : 변경 전 양정 [m],               H2 : 변경 후 양정 [m]

              N1 : 변경 전 회전수 [rpm],        N2 : 변경 후 회전수 [ℓ/rpm]

              D1 : 변경 전 관경 [㎜],              D2 : 변경 후 관경 [[㎜]

​

 ③ 축동력 : 펌프의 축동력은 회전수의 세제곱 및 관경의 오제곱에 비례한다.​

  여기서, P1 : 변경 전 축동력 [kW],              P2 : 변경 후 축동력 [kW]

              N1 : 변경 전 회전수 [rpm],             N2 : 변경 후 회전수 [ℓ/rpm]

              D1 : 변경 전 관경 [㎜],                   D2 : 변경 후 관경 [[㎜]

​

14. 펌프의 이상현상

가. 공동현상 (Cavitation)

  1) 공동현상 (cavitaion) : 펌프흡입측 배관 내의 물의 정압이 기존 증기압 보다 낮아져 기포가 발생되어 물이 흡입되지

                                            않는 현상을 말한다.

  2) 공동현상의 발생원인

    ① 펌프의 흡입수두(양정)이 큰 경우

    ② 펌프의 설치 위치가 수면 보다 높은 경우

    ③ 펌프의 마찰손실이 클 경우

    ④ 펌프의 임펠러 속도가 클 경우

    ⑤ 펌프흡입측 배관의 구경이 작을 경우

    ⑥ 배관내의 수온이 높을 경우

    ⑦ 내관내의 물의 정압이 기존의 증기압 보다 낮을 경우

  3) 공동현상 방지 대책

    ① 펌프의 흡입수두(양정)을 작게 한다.

    ② 펌프의 설치위치를 수면보다 낮게 한다.

    ③ 펌프의 마찰손실을 작게 한다.

    ④ 펌프의 임펠러 속도를 작게 한다.

    ⑤ 펌프 흡입측 배관의 구경을 크게 한다.

    ⑥ 양 흡입펌프를 사용한다.

    ⑦ 배관내의 물의 정압이 기존의 증기압 보다 높게 한다.

  4) 발생현상

    ① 펌프의 임펠러를 소손시킨다.

    ② 소음과 진동이 발생한다.

    ③ 펌프의 성능이 저하된다.

    ④ 배관의 부식을 초래한다.

​

나. 수격현상 (Water hammering)

  1) 수격현상 (Water hammering) : 배관내의 물의 흐름에서 급격히 밸브를 개폐하였을 경우 발생하는 충격현상을 말한다.

  2) 수격현상의 발생 원인

    ① 급격하게 밸브를 개폐할 경우

    ② 정상 운전시 유체의 압력 변동이 있을 때

    ③ 펌프를 갑자기 정지할 때

  3) 수격현상 방지대책

    ① 배관내의 유속을 낮게 한다.

    ② 배관의 구경을 크게 한다.

    ③ 펌프 토출측 가까운 곳에 밸브를 설치한다.

    ④ 조압수조 (Surge tank)를 설치한다.

    ⑤ 수격방지기 (Water hammering cushion) 또는 에어챔버 (Air chamber)를 설치 한다.

    ⑥ 플라이 휠 (Fly wheel)을 설치한다.

​

다. 맥동현상 (Surging)

  1) 맥동현상 (Surging) : 유량이 단속적으로 변하여 펌프 흡입측 및 토출측에 설치된 진공계(연성계) 및 압력계가 흔들리

                                         고 진동과 소음이 발생하여 펌프의 토출유량이 변하는 현상을 말한다.

  2) 맥동현상 발생원인

    ① 펌프의 성능곡선이 산 모양이고 운전점이 그 정상부에 있을 경우

    ② 배관 도중에 수조가 있을 경우

    ③ 배관내 기체 상태의 부분이 있을 경우

    ④ 유량조절밸브가 배관 중 수조의 후방에 위치해 있을 경우

  3) 맥동현상 방지 대책

    ① 운전점을 고려하여 적정한 펌프를 선정한다.

    ② 배관도중에 불필요한 수조를 설치하지 않는다.

    ③ 배관내 기체를 없앤다.

    ④ 유량조절밸브를 배관 중 수조의 전방에 설치한다.

    ⑤ 회전차나 안내깃의 형상치수를 바꾸어 그 특성을 변화시킨다.

​

5. 르 샤틀리에 공식

  ▣ 르 샤틀리에 공식은 혼합가스의 폭발 가능성을 측정하는 지표이다.

  여기서, U (L) : 혼합가스의 연소(폭발) 상 · 하한계

              V1, V2, V3 : 연소(폭발) 가스의 부피 비율 (조성농도)

              U1 (L1), U2 (L2), U3 (L3) : 연소(폭발) 가스의 상 · 하한계

​

16. 스케줄 수 (Schedule No.)

가. 스케줄 수 (번호)​

나. 안전율​

17. 신축이음

  ① 슬리브형     ② 벨로스형     ③ 루프형     ④ 스위블형     ⑤ 볼조인트

​

18. 관부속품

  ① 엘보      ② 티 :  ㉠ 직류티,  ㉡ 분류티(측류티)     ③ 리듀서     ④ 캡

  ※ 편심리듀서 : 펌프 흡입측 배관의 공기고입을 방지하기 위하여 사용한다.

                           (한쪽으로만 배관이 작아지는 모양)

​

19. 밸브

   ① OS & Y 밸브 : 개폐표시형 밸브

   ② 버터플라이 밸브 : 흡입배관에는 사용하지 않는다. 난류발생

   ③ 글루브 밸브 (유량조절밸브) : 유체의 흐르는 방향이 180 [°]

   ④ 앵글밸브 (Angle valve) : 유체 흐름의 방향이 90 [°]인 밸브

   ⑤ 체크밸브 (Check valve)

        ㉠ 리프트형         ㉡ 스윙형

  ※ 스모레스키 밸브 : 리프트형 체크밸브에 디스크가 달려 충격을 완화시키는 작용을 하는 밸브

  ⑥ 후드 밸브 : 체크밸브 + 여과기능

  ⑦ Y형 스트레이이너 (이 물질 제거)​