1. 연속방정식
▣ 유체는 특이한 성질이 많다. 유체의 성질에 대한 법칙중에서 유체가 특정한 관을 끊이지 않고 연속하여 흐르고 관과
유체간에 마찰이 없다고 가정을 하면 다음과 같은 연속방정식이 성립하게 된다.
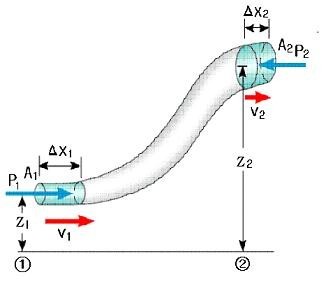
위와 같은 조건에서는 유체는 관 노선 전체에 대하여 같은 시간에 같은 부피만큼 흐른다. 관이 중간에 구경이 커지든, 작아
지든 관계없이 같은 시간에는 같은 부피 만큼 흐르게 된다.
부피1 = 부피2, V1 = V2 이다.
흐르는 유체가 물이라고 하고 물의 온도가 일정하다고 가정하면 물의 밀도도 같게 된다.
밀도1 = 밀도 2, ρ1 = ρ2
그런데 밀도 = 질량 / 부피이므로 밀도와 부피가 같다면 질량도 같게 된다.
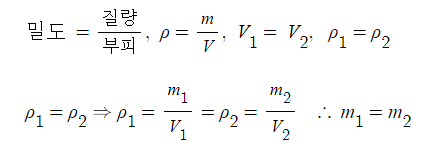
이상의 내용을 정리하면 어떤 유체가 연속적으로 관을 따라 흐를 때 특정시간 동안 관을 따라 흐른 유체의 부피, 질량, 밀도는 관의 굵기 (관경)에 관계없이 어느 지점에서나 일정하다는 것을 알 수 있다.

위와 같은 사실을 토대로 관의 어느 특정 지점에서 유체가 흐르는 속도를 알 수 있게 된다.
유체가 흐른 부피는 관의 굵기(단면적)과 유체가 흐른 거리를 곱한 값이 된다. 유체가 이동한 거리는 유체의 속도와 시간의 곱이 된다. 그런데 유체가 연속하여 흐르는 관에서는 특정시간 동안 유체가 흐른 부피는 관의 어느 지점에서나 같다고 하였으므로 다음과 같은 식이 성립하게 된다.

위 식을 통해 동일 관에서 흐르는 유체의 속도는 관의 단면적에 반비례함을 알 수 있다.
위에서 말한 동일 관을 흐르는 유체는 관의 단면적에 관계없이 어느 지점에서나 동일 시간에 흐르는 부피, 밀도, 질량이 일정하고 유체의 흐르는 속도는 관의 단면적에 반비례한다는 것을 나타내는 식을 연속방정식이라고 한다.
2. 베르누이의 법칙
앞서 특정한 관속의 흐르는 유체의 성질을 연속방정식을 통해 알아 보았다. 그런데 베르누이는 연속방정식으로 알아 본 유체와 성질과 열역학 제1법칙 즉 에너지 보존의 법칙을 이용하여 유체의 특성을 설명하고 있는데 이를 베르누이의 법칙이라고 한다. 베르누이의 법칙에 대하여 상세하게 알아 보자.
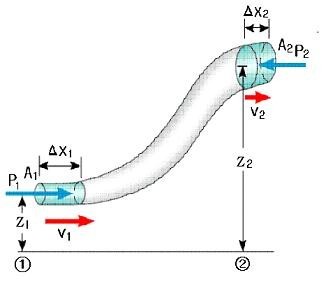
에너지보존의 법칙에 따르면 위 그림 ①에서와 와 ②에서의 유체가 갖은 에너지의 총 합은 같게 된다. 그런데 유체가 갖는 에너지는 유체가 하는 일과 속도에너지, 위치에너지로 구성된다. 여기서 일과 에너지는 같은 것이고 ①과 ②에서 유체는 동일한 압력하에서 부피가 변화는 것으로 보면 일을 했다고 본다. 이를 에너지 보존의 법칙식으로 나타내면 다음과 같다.

위 식에 부피(V)로 양변을 나누게 되면 다음과 같은 식이 성립한다.
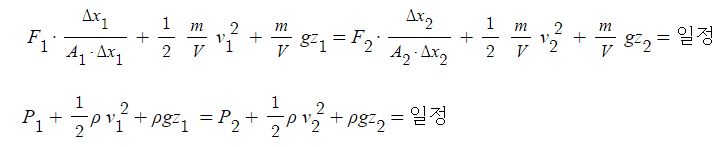
위 식에서 위치에너지가 일정 (관이 수평으로 평행)하다면 다음과 같은 식이 된다.
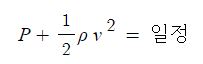
즉 관 내부의 압력과 유체의 속도는 반비례함을 알수 있다.
또한 앞 식을 ρg로 나누면 다음의 식이 성립한다.
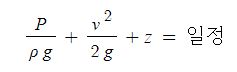
3. 수력기울기 (수력구배)
위에서 설명한 바와 같이 유체에 있어서는 에너지 일반식이 수두의 식으로 표현됨을 알 수 있다. 이러한 수두식은 아래 그래프와 같이 나타낼 수 있고 이를 통해 수력구배에 대하여 알아 보자.
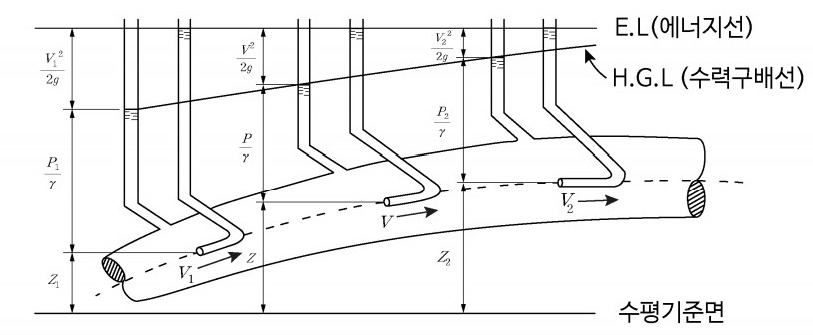
위 그림에서 관내에 마찰이 없다고 하면 전수두는 에너지 보존의 법칙에 따라 일정하고 그림 처럼 수평이 될 것이다. 여기서 전수두란 압력수두, 속도수두, 위치수두를 합한 값이다.
그런데 압력수두와 위치수두의 합을 피에조미터 수두라고 하고 이는 전수두에서 속도수두의 값을 뺀 값이고 이것을 높이로 나타낸 값이 수력기울기선이다. 만약 유체의 진행방향으로 관의 지름이 점차 커진다면 유체의 진행 방향으로 속도가 작아지게 되고 따라서, 속도수두는 작아지는데 에너지선은 일정하므로, 일정한 에너지선에서 속도수두를 뺀 수력기울기선 (수력구배선)은 우상향하게 된다. 또한 속도구배선은 에너지선에서 속도수두를 뺀 것이기 때문에 항상 에너지선 아래에 위치하게 된다.
⊙ 압력수두(Pressure head) : P / ρg 를 압력수두라고 하며, 압력을 유체의 높이로 나타낸 것이다. 압력수두를 접압수두
(Static pressure head)라고도 한다.
⊙ 속도수두 (Velocity head) : v2 / 2g 을 속도수두라고 한다. 유체의 속도에너지를 유체의 높이로 나타낸 것이다.
⊙ 위치수두 (Elevation head) : Z 를 위치 수두라고 한다. 유체의 위치가 갖는 에너지를 말한다. Potential energy라고도
한다.
⊙ 전수두 (Total head) : H를 전수두라고 하며, 압력수두, 속도수두, 위치수두의 합이다.
⊙ 피에조미터 수두 (Piezometric head) : P/ρg + Z 를 피에조미터 수두라고 한다. 압력수두와 위치수두의 합이다.
유체가 흐르는 위치에 피에조미터를 설치했을 때 피에조미터에 액체가 올라가는 부분까지
의 높이에 해당하는 수두를 의미한다.
#유체 #연속방정식 #베르누이 #압력수두 #속도수두 #위치수두 #에너지보존법칙 #관경
#구경 #피에조미터 #포텐셜에너지 #정압수두 #수력구배선 #수력기울기선
'소방설비기사 기계실기 이론' 카테고리의 다른 글
| 소방설비 도시기호 (0) | 2023.10.12 |
|---|---|
| 달시의 법칙 (Darcy's law) (0) | 2023.09.18 |
| 소방 유체역학 공식 정리 - 2 (4) | 2023.09.14 |
| 소방 유체 역학 단위 정리 (2) | 2023.09.12 |
| 소방시설의 종류 (0) | 2023.09.09 |
