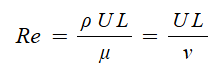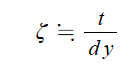아낌없이 주는 나무

1. 펌프의 분류

가. 원심펌프 (Centrifugal pump)

  ▣ 원심펌프는 Vane (Blade)이 달린 임펠러 (Impeller)가 밀폐된 케이싱 (Casing)내에서 회전함으로써 발생하는 원심력을

       이용하여 비압축성 유체를 이송하거나 압력을 높여 주는 회전기기이다.

  ▣ 원심펌프에서 유체를 이동시키는 원력력은 압력이다.

 <원심펌프의 원리>

   ① 유체는 Impeller 중심에서 강제로 유입된다.

   ② 베인 (Vane)을 따라 반지름 방향으로 흐르는 사이에 유체는 운동에너지를 얻는다.

   ③ 유체가 볼류트 (Volute)를 통과하는 사이에 운동에너지가 압력에너지로 변환된다.

  ▣ 축류 펌프는 다수 (보통 3~5)의 깃을 가진 회전차를 동력장치에 직접 연결하여 작은 용량으로 큰 유량을 수송할 수

       있게 설계된 펌프이다.

​

다. 왕복펌프 (Reciprocating pump)

   ▣ 왕복펌프는 펌프를 구성하고 있는 피스톤 등의 왕복운동에 의해 실린더 내를 진공에 가까운 압력상태로 만들어 낮은

        곳에 있는 물을 흡입하고 여기에 압력을 가하여 필요한 거리로 수송하는 설비를 말한다.

​

2. 펌프의 양정 및 동력

  ▣ 펌프의 전양정 = 흡입양정 + 토출양정 + 관내 마찰손실수도

    ⊙ 펌프의 실양정 = 흡입양정 + 토출양정

가. 펌프 양정의 구성

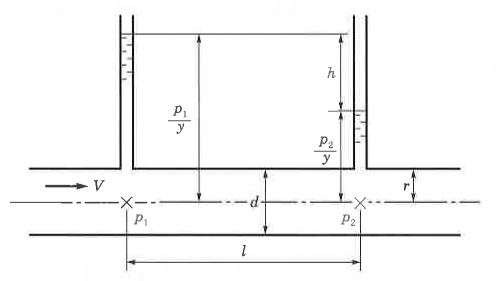
  ① Weisbach - Darcy의 마찰손실 공식​​

     여기서, △h : 배관의 마찰손실수두 (mAq),             f : 관의 마찰손실계수

                  L : 배관의 길이 (m) U : 유속 [m/sec]          D : 배관의 직경 [m] g : 중력가속도 (9.81 m/sec2)

      ∴ 압력손실수두 : P = γh 를 적용시키면​​

  ② 하젠 - 윌리암스의 식​

      여기서, △P : 마찰손실압력 (kgf / ㎠),        Q : 유량 (ℓ/min, lpm),           D : 관경 [㎜]

                   L : 배관의 길이 (linear 및 상당길이의 합),         C : 관벽의 조도에 의한 계수

  ③ 흐름에서의 미소손실 : 관이 휘어지거나 관의 중간에 엘보(elbow), 조인트 (joint), 밸브 (valve) 등과 같은 부속들을 사용

                  하여 관에서의 단면의 형태가 변화되는 곳에서 발생하는 손실을 미소손실이라고 한다. 미소손실에 의한 손실

                  수두 HL은 다음과 같다.​

          여기서, HL : 손실수두,        K : 미소손실수두계수,      U2/(2g) : 속도수두

​

나. 펌프 소요동력의 산출

  ▣ 힘(F)은 질량(m)에 가속도(g)가 가해진 값이며, 일(W)은 힘(F)에 거리 변화가 발생한 값과 같다.

       또한 동력은 일(W)을 시간으로 나눈 값과 같은 의미를 가진다.

       그러므로 유체를 수송하는 펌프의 동력값에 대해 살펴보면 다음과 같이 나타낼 수 있다.​

  ▣ 펌프의 효율이 η이고 축동력 전달계수를 K라고 하면 펌프의 동력값은 다음과 같다.​

     여기서, P : 동력(kW),          Q : 정격 토출량 (㎥/min),              H : 양정 (유체 이송 높이) [m]

                   η : 펌프의 효율,     K : 축동력 전달계수 (보통 1.1을 사용)

​

3. 펌프에서 발생하는 현상

가. 공동현상 (cavitation)

  ▣ 액체 속을 고속도로 움직이는 물체의 표면은 액체의 압력이 저하하는데, 이 때의 압력이 액체의 포화 증기압 보다 낮아

       진 범위에 증기가 발생하거나 액체 속에 녹아 있던 기체가 나와서 공동현상을 이룬다.

       이것은 수력터빈이나 선박용 프로펠러를 운전할 때 자주 발생하는 현상으로 압력 면에 발생하는 경우도 있지만,

       주로 날개의 등 부분에 발생한다. 발생한 기포는 압력이 높은 부분에 이루면 급격히 부서져 소음이나 진동의 원인이

       되며, 터빈이나 프로펠러의 효율을 떨어뜨린다.

  ① 발생원인

     ㉠ 펌프 임펠러 깃에서 물의 압력이 포화증기압 이하로 내려가면 증발하여 기포가 발생한다.

     ㉡ 펌프의 흡입측 낙차가 클 경우

     ㉢ 이송하는 유체가 고온일 경우

     ㉣ 펌프의 마찰손실이 클 경우

     ㉤ 임펠러 속도가 지나치게 클 경우

  ② 발생현상

     ㉠ 소음과 진동이 발생한다.

     ㉡ 펌프의 성능 (토출량, 양정, 효율)이 감소한다.

     ㉢ 임펠러 (Impeller)의 침식이 발생한다.

     ㉣ 심하면 양수불능상태가 된다.

  ③ 방지대책

     ㉠ 펌프 내에서 포화증기압 이하의 부분이 발생하지 않도록 조치한다.

     ㉡ 펌프의 설치위치는 가능한 낮게 한다.

     ㉢ 펌프의 회전수를 낮추고, 흡입 비속도를 크게 한다.

     ㉣ 펌프의 마찰손실을 작게 한다.

     ㉤ 펌프의 유량을 줄이고 양흡입펌프를 사용한다.

​

나. 수격 작용 (Water hammering)

  ▣ 관 내를 흐르고 있는 물의 유속이 바뀌면 유체의 운동에너지가 압력에너지로 변하여 관내 압력이 상승하게 되어 배관

       과 펌프에 손상을 주는 현상으로 수격작용은 펌프의 운전중은 물론이고 펌프가 정지될 때도 발생할 수 있으므로 대용

       량인 펌프와 배관이 길어지는 경우에는 적절한 대비책이 있어야 한다.

  ① 발생원인

     ㉠ 정전 등으로 갑자기 펌프가 정지할 경우

     ㉡ 밸브를 급히 개폐할 경우

     ㉢ 펌프의 정상운전시 유체의 압력 변동이 있는 경우

  ② 발생현상

     ㉠ 압력상승에 의해 펌프, 밸브, 플랜지, 관로 등 여러 기기가 파손된다.

     ㉡ 압력강하에 의해 관로가 압괴하거나 수주분리가 생겨 재결합시에 발생하는 격심한 충격파에 의해 관로가 파손된다.

     ㉢ 소음과 진동의 원인이 된다.

     ㉣ 주기적인 압력변동 때문에 자동제어계 등 압력을 컨트롤하는 기기들이 난조를 일으킨다.

  ③ 방지대책

     ㉠ 관경을 굵게 하여 가능한 한 유속을 느리게 한다.

     ㉡ 펌프 회전축에 플라이휠(Flywheel)을 설치하여 펌프의 급속한 속도변화를 방지한다.

     ㉢ 펌프의 토출측에 조압수조(Surge tank) 또는 수격 방지기(water hammering cusion)를 설치한다.

     ㉣ 유량조절 밸브를 펌프 토출측 직후에 설치하고 적당한 밸브 제어를 한다.

​

다. 맥동현상 (Surgeing)

  ▣ 펌프의 운전중에 압력계기의 눈금이 어떤 주기를 가지고 큰 진폭으로 흔들림과 동시에 토출량은 어떤 범위에서 주기적

       으로 변동이 발생하고 흡입 및 토출 배관의 주기적인 진동과 소음을 수반한다. 이를 맥동(Surging)현상이라 한다.

  ① 발생원인

     ㉠ 펌프의 H - Q 곡선이 오른쪽 상승부에서 운전 시

     ㉡ 펌프의 토출관로가 길고, 배관 중간에 수조 또는 기체가 존재 시

     ㉢ 수조 또는 기체상태가 잇는 부분의 하류측 밸브에서 토출량을 조절 시

  ② 발생현상

     ㉠ 흡입 및 토출 배관에 주기적인 진동과 소음이 발생한다.

     ㉡ 한번 발생하면 그 변동주기는 비교적 일정하고, 송출밸브로 송출량을 조작하여 인위적으로 운전상태를 바꾸지 않는

          한 이 상태가 지속된다.

  ③ 방지대책

     ㉠ 펌프의 H - Q 곡선에 오른쪽 하향구배 특성을 가진 펌프를 채용한다.

     ㉡ 회전차나 안내깃의 형상 치수를 바꾸어 그 특성을 변화시킨다.

     ㉢ 바이패스관을 사용하여 운전점이 펌프 H-Q 곡선의 오른쪽 하향구비 특성 범위 위치에 오도록 한다.

     ㉣ 배관 중간에 수조 또는 기체 상태인 부분이 존재하지 않도록 배관한다.

     ㉤ 유량조절밸브를 펌프 토출측 직후에 위치시킨다.

     ㉥ 불필요한 공기탱크나 잔류공기를 제어하고, 관로의 단면적, 유속, 저항 등을 바꾼다.

​

#펌프 #양정 #캐비테이션 #공동현상 #수격현상 #맥동현상 #마찰손실계수 #다르시 #하젠 #윌리암스

#펌프출력 #안내깃 #임펠러

1. 층류와 난류

 가. 층류

   ① 평균 유속에 정비례한다.

   ② 흐름이 닿은 벽면의 조도에 거의 관계 없다.

   ③ 유체의 점성계수 (μ)에 정비례하므로 온도에 의해 많은 영향을 받는다.

나. 난류

   ① 평균 유속의 약 2제곱에 비례한다.

   ② 흐름에 접하는 벽면의 조도에 의해서 크게 다르다.

   ③ 유체의 점성계수 (μ)에 영향을 받으나 층류의 경우처럼 심하지는 않다.

​

2. 레이놀즈의 수

  ▣ 레이놀즈는 실험을 통하여 층류, 난류의 구분이 속도 (U)에 의해서만 결정되는 것이 아니고 유체의 점성계수(μ), 밀도

       (ρ), 관의 관경 (d)에도 관계됨을 알았다. 이들 변수에 의한 무차원함수를 정의하였는데

       이 함수를 레이놀즈수 (Re)라 부르며, 이에 대한 일반식은 다음과 같다.

           여기서, ρ : 유체의 밀도, U : 유체의 특성속도, L : 특성길이

                        μ : 유체의 점성계수, v : 유체의 동점성계수

  ▣ 무차원수인 Re가 작을 때의 흐름은 층류이며, Re가 커지면 난류로 변하는데

       이 때의 천이점의 Re를 임계 Reynolds 수 (Critical Reynold's number) Rec라고 한다.

​

3. 바이스바흐 - 달시 (Weisbach - Darcy)의 식

  ▣ 다음 그림과 같은 내경 d인 관로속을 평균 유속 V로 유체가 흐르고 있을 때 임의의 거리 l 만큼 떨어진

       두 점의 압력을 p1, p2라 하면 유체의 마찰에 의한 압력손실 hL은 다음 식으로 표시된다.

   ▣ 바이스바흐 - 달시의 유체마찰손실

    이를 Weisbach-Darcy 의 식이라 부르고, λ를 관 마찰계수라 부른다.

​

4. 관 마찰계수의 실용식

  ▣ 보통의 철관 등에 있어서는 관벽 돌기의 간격이 다르거나, 또는 작은 돌기 사이에 큰 것들이 섞여 있는

       경우가 많기 때문에 관마찰계수는 다음 Mises의 실험식으로 구한다.​

    ▣ Scobey의 실험식은 다음과 같다.​

      여기서, d의 단위는 m이고, 콘크리트관에 적용하며, 정수 c의 값은 다음과 같다.

       ⊙ 내면이 매끈한 콘크리트관 : c = 0.156

       ⊙ 연결된 콘크리트관으로서 수년간 사용한 것 : c = 0.218

       ⊙ 특히 조심성 없이 연결된 관 : c = 0.029

​

5. 원관(둥근관) 이외의 관 마찰

  ▣ 단면이 원형이 아닌 관의 관마찰을 생각할 경우에는 관의 단면적을 A, 그 단면의 젖은 길이를 lw, 관의

       길이 l 사이의 압력손실을 △p, 관 단면의 평균유속을 V라 하고, 흐름은 관측과 평행인 것으로 생각하여

       관벽의 평균 횡응력 τ 를​​

     v는 수두손실이 생기는 곳의 영향을 받지 않는 단면에 있어서의 평균유속이고, 손실이 생기는 곳의 전후에

      평균유속이 변화할 대 일반적으로 큰 쪽의 유속을 사용한다.

​

 가. 관로가 급히 넓어질 때 (급확대관)

   ▣ Borda - Carnot의 수두 손실

 나. 관로가 급속히 좁아질 때 (급속축소관)​​

 다. 밸브(valve)와 콕(cock)에 의한 손실

   ▣ 관로 속의 유량 또는 흐름의 방향을 제어 (control)하기 위하여 각종 밸브가 사용되는데, 그 손실수두는 밸브가 달린

        부분에서 흐름의 단면적이 변화하기 때문에 생기며, 그 크기는

      으로 표시된다. 단, V는 관로 속에서 밸브의 영향을 받지 않는 곳에서의 평균유속이다.

  ① 슬루스 밸브 (sluice valve) : 슬루스 밸브에 있어서는 주로 밸브 선단의 직후에 있어서 흐름의 단면적이 급속히 확대됨

                                                     으로 인하여 수두손실이 생긴다.

  ② 글로브 밸브 (globe valve) : 다음 그림의 글로브 밸브에 있어서도 x/d1이 커질수록 ζ는 작아지지만 완전히 열었을 때

                                                    도 ζ는 6 ~ 8의 값을 가진다.

  ③ 너비 너트 밸브 (Butterfly valve) : 이 밸브에 있어서는 밸브만의 경사각 θ 가 커지면 밸브 직후의 단면적의 급증이

                                                              현저해져서 손실계수 ζ가 커진다.

                                                              원형 나비 너트 밸브에서 θ = 0 일 때는 다음과 같다.

               이다. 단, t, dy는 밸브 원관 (둥근관)의 두께와 지름이다.

  ④ 콕 (cock) : 콕에 있어서도 각 θ 의 증가와 함께 흐름의 단면적의 변화가 현저해지고, 손실계수  ζ 는 커진다.

#층류 #난류 #레이놀즈수 #다르시 #달시 #바이스바흐 #마찰계수 #손실수두 #버터플라이 #글로브밸브

#콕 #점성계수 #동점성계수

Darcy's Law : 달시의 법칙

​

1856년 프랑스인 다르시(H. Darcy)가 여과사(濾過沙)의 실험에서 발견한 법칙으로

한마디로 말하면 모래로 가득 채운 원통에 물을 통과시키는데 필요한 압력과 원통의 길이와의 관계를 나타내는 식을 말한다.

즉, 다공성 매질(모래)를 통과하는 수량(물의 양)이 압력과 원통의 길이에 따라 얼마나 달라 지는가를 나타내는 식이다.

​

다르시는 모래 내부에서 물의 움직임을 규명하기 위해 실험을 하였다.

시간(t) 동안 모래 단면적 A를 통하여 흐른 물의 체적(수량, Vol), 수두(水頭, h1과 h2)를 측정한 결과 물의 체적(수량, Vol)과 다른 요소들 사이에는 일정한 관계법칙이 있음을 발견하였다.

​

Darcy는 모래층을 통과하는 물의 유동을 연구하던 중에 모래층을 통과하는 물의 유량 Q는 모래층의 지점1의 수두 h1과 지점2의 수두 h2의 차에 비례하고, 1, 2 지점간의 거리 L에 반비례하며, 단면적 A와 매질의 성질에 따라 좌우되는 계수 K 즉, 수리전도도에 비례함을 알아 냈다.

다르시의 법칙은 다공성 매질을 통과하는 유체의 단위 시간당 유량과 유체의 점성, 유체가 흐르는 거리와 그에 따른 압력 차이 사이의 비례관계를 보여준다. 유체로 포화된 다공성 물질(多孔性物質) 매체 속을 통과하는 수량(水量)은 수두손실(水頭損失)에 비례하고 통과하는 매체의 거리에 반비례한다는 것을 보여준다.

유량 Q (㎥/s)는 매질의 투과율 (Permeability, K), 물이 흐르는 매질의 내부 단면적 A과 유체가 흐르는 두 점간 압력차이 (Pb - Pa)의 곱을 유체가 흐르는 길이(ℓ)로 나눈 것과 같다. 음의 기호는 압력이 낮아지는 방향으로 유체가 흐른다는 것을 의미한다.

여기서 투수계수는 유체의 점성, 매질의 특성 (흙 입자의 크기와 모양, 배열 상태, 포화도,

간극비 등)과 관련 되어 정해지는 값이다.

​

적용범위

​

다르시의 법칙은 유속이 느린 점성 흐름에 대해서만 유효한데 대부분의 흐름에는 다르시의 법칙을 적용할 수 있다. 일반적으로 레이놀즈 수가 1보다 작은 흐름은 층류이고 다르시의 법칙을 적용할 수 있으며 실험에 의하면 레이놀즈수가 약 10 정도인 흐름까지도 다르시의 법칙을 적용할 수 있다.

​

#달시 #다르시 #유체 #손실수두 #유량 #압력 #매질 #투과율 #단면적 #길이 #레이놀즈

Darcy's Law : 달시의 법칙

​

1856년 프랑스인 다르시(H. Darcy)가 여과사(濾過沙)의 실험에서 발견한 법칙

한마디로 모래로 가득 채운 원통에 물을 통과시키는데 필요한 압력과 원통의 길이와의 관계를 나타내는 식이다.

즉, 다공성 매질(모래)를 통과시하는 수량(물의 양)이 압력과 원통의 길이에 따라 얼마나 될지를 나타내는 식이다.

​

달시는 모래 내부에서의 물의 움직임을 규명하기 위해 실험을 하였다. 시간(t) 동안 모래 단면적 A를 통하여 흐른 물의 체적(수량, Vol), 수두(水頭, h1과 h2)를 측정한 결과 물의 체적(Vol)과 다른 요소들 사이에는 관계법칙이 있음을 발견했다.

​

Darcy는 모래층을 통과하는 물의 유동을 연구하던 중에 모래층을 통과하는 물의 유량 Q는 모래층의 지점1의 수두 h1과 지점2의 수두 h2의 차에 비례하고, 1,2 지점간의 거리 L에 반비례하며, 단면적 A와 매질의 성질에 따라 좌우되는 계수 K 즉, 수리전도도에 비례함을 알아 냈다.

다르시의 법칙은 다공성 매질을 통과하는 유체의 단위 시간당 유량과 유체의 점성, 유체가 흐르는 거리와 그에 따른 압력 차이 사이의 비례관계를 보여준다. 유체로 포화된 다공성 물질(多孔性物質) 매체 속을 통과하는 수량(水量)은 수두손실(水頭損失)에 비례하고 통과하는 매체의 거리에 반비례한다는 것을 보여준다.​

유량 Q (㎥/s)는 매질의 투과율 (Permeability, K), 물이 흐르는 매질의 내부 단면적 A과 유체가 흐르는 두 점간 압력차이 (Pb - Pa)의 곱을 유체가 흐르는 길이(ℓ)로 나눈 것과 같다. 음의 기호는 압력이 낮아지는 방향으로 유체가 흐른다는 것을 의미한다.

여기서 투수계수는 유체의 점성, 매질의 특성(흙 입자의 크기와 모양, 배열 상태, 포화도,

간극비 등)과 관련 되어 정해지는 값이다.

​

적용범위

다르시의 법칙은 유속이 느린 점성 흐름에 대해서만 유효한데 대부부느이 흐름에는 다르시의 법칙을 적용할 수 있다. 일반적으로 레이놀즈 수가 1보다 작은 흐름은 층류이고 다르시의 법칙을 적용할 수 있으며 실험에 의하면 레이놀즈수가 약 10 정도인 흐름까지도 다르시의 법칙을 적용할 수 있다.

​

#달시 #다르시 #유체 #손실수두 #유량 #압력 #매질 #투과율 #단면적 #길이 #레이놀즈