아낌없이 주는 나무

나. 유도기전력의 방향 (렌쯔의 법칙)

 ▣ 코일을 통과하는 자속에 변화를 주면 코일에 발생하는 유기기전력의 방향은 자속의 변화를 방해하려는 방향으로

     발생한다. 이것을 유도 기전력에 관한 렌쯔의 법칙(Lenz's law)이라 한다.

다. 유기기전력의 크기 (페러데이 법칙)

 ▣ 코일을 감아주고 전류를 흐르게 하면 코일 내부에 자속 ф가 발생한다. 이번에는 반대로 코일을 감아 주고

      이 코일 내부로 자속 ф 를 공급해 준다. 즉, 감겨진 코일에 자석의 N극을 가까이 접근 시켜 자속 ф를 공급해 준다.

      이렇게 하면 가만히 있던 코일에 전류가 흐르게 되는데 전류가 흐른다는 것은 전압, 즉 유기기전력이 생겼다고

      볼 수 있다. 이 처럼 자속에 의해 전압 (기전력)이 생기는 현상을 '전자유도' 또는 '전자유도현상' 이라고 한다.

      그러면 이 때 유기되는 기전력의 크기는 어떻게 산정할까?

 ▣ 외부의 자계에 의하여 코일에 발생하는 기전력을 유도기전력 또는 유기기전력이라고 하는데 이 유기기전력이 얼마나

      발생했는지를 나타내는 식이 패러데이의 법칙(Faraday's law)이다. 패러데이의 법칙은 다음 수식과 같다.

 ▣ N은 코일을 감은 권수이고 t는 시간, ф는 쇄교자속을 나타낸다. 쇄교는 코일 사이를 통과하는 의미이다.

     d는 변화량을 의미하며 dt는 시간의 변화량, dф는 자속의 변화량을 의미한다. 따라서 dф / dt 는 쇄교자속의 시간에

     따른 변화량을 의미한다.

 ▣ 정리하면 코일 내부에 자속이 변화하면 유도기전력이 생기는데 그 크기를 나타낸 것이 패러데이의 법칙(Faraday's law)

      이다. 유도기전력의 크기는 코일을 감은 권수 N에 비례하고 쇄교자속의 시간에 따른 변화율에 비례한다.

​

2. 움직이는 도체에 의한 유도기전력의 크기와 방향

가. 유도기전력의 크기

 ▣ 앞서 패러데이 법칙을 설명할 때 코일에 자석을 움직여 자속을 변화를 주면 유도기전력이 발생한다고 설명했다.

      이번에 자석에 의해 자기장을 형성해 놓고 이곳에 코일을 움직여 자속을 코일 선이 끊어 주어도 자속이 변화를

      일으켜도 패러데이의 법칙에 의하여 코일에 유도기전력이 발생한다.

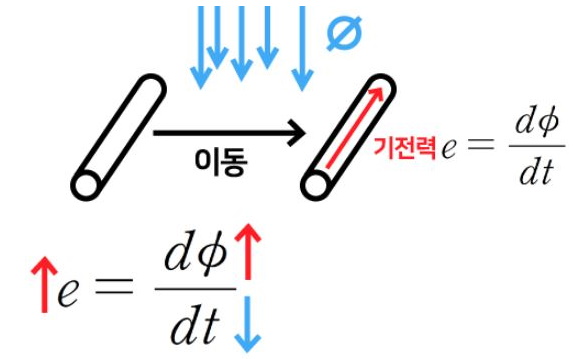
 ▣ 기전력은 패러데이의 전자유도 법칙에 따라 발생한다. 시간당 자속변화가 있으면 도체에 기전력이 발생한다는 것이다.

      이 때 기전력은 자속이 많이 있거나(혹은 자속의 변화가 크거나), 도체가 지나가는 속도가 빠를수록 (혹은 자속변화

       시간이 짧을 수록) 커진다.

 ▣ 자속밀도 B는 단위 면적 A당 자속 ф 이므로 면적을 이항하면 자속 ф는 자속밀도 B와 면적 A의 곱으로 치환할 수 있다.

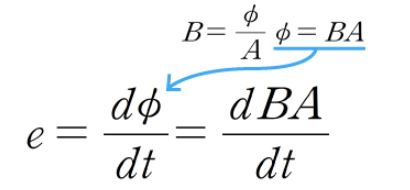
 ▣ 여기서 면적 A는 도체와 자속이 쇄교한 면적을 말한다. 즉, 도체의 유효길이ℓ [m]와 도체가 이동한 거리를 곱하면

      면적이 되는데, 도체의 이동거리는 도체의 이동속도 v [m/s]와 시간[s]를 곱하여 구할 수 있다. (시속 100[㎞/h]로

      1시간을 간다면 100×1=100 [㎞]를 이동했다는 것을 알 수 있듯이 말이다)

【 출제 예상 문제 】

​

1. 코일을 지나가는 자속이 변화하면 코일에 기전력이 발생한다. 이 때 유기되는 기전력의 방향을 결정하는 법칙은 ? ①

    ① #렌츠 의 법칙       ② #플레밍 의 왼손법칙          ③ #키르히호프 의 제2법칙     ④ 플레밍의 오른손 법칙

[해설] 렌츠의 법칙 : 전자유도현상에서 코일에 생기는 유도기전력의 방향 결정

​

2. 전자유도현상에 의하여 생기는 유도기전력의 크기를 결정하는 법칙은 ? ② 

   ① #렌츠 의 법칙                ② 페러데이의 법칙            ③ 앙페르의 법칙          ④ 플레밍의 오른손 법칙

[해설] 페러데이의 전자유도법칙

    ① 자속변화에 의한 유기기전력의 크기 결정

    ② 전자유도현상에 의하여 생기는 유도기전력의 크기를 나타내는 법칙

​

3. 자기장 중에서 도체가 운동할 때 도체에 유기되는 기전력의 방향을 결정하는법칙은 ? ②

   ① #플레밍 의 왼손법칙   ② 플레밍의 오른손 법칙  ③ 페러데이의 법칙    ④ #암페어 의 오른 나사 법칙

[해설] 플레밍의 오른손 법칙 : 도체 운동에 의한 유기기전력의 방향 결정 : 오발, 오른손 발전기, 왼손 전동기

​

4. 1회 감은 코일에 지나가는 자속이 1/100 [sec] 동안에 0.3[Wb]에서 0.5[Wb]로 증가 하였다면 유도되는 기전력은

    몇 [V]인가 ? ③

    ① 5.0 [V]               ② 10[V]                    ③ 20[V]                      ④ 40 [V]

[해설] #전자유도 법칙에 의한 코일의 유도기전력 e = N dф/dt = 1× (0.5-0.3)÷ 1/100 = 20 [V]

​

5. #플레밍 의 오른손법칙에서 중지 손가락의 방향은 ? ③

    ① 운동방향           ② 자속밀도의 방향               ③ 유도기전력의 방향              ④ 자력선의 방향

[해설] 플레밍의 오른손 법칙 : 엄지 - 도체의 운동방향, 검지 - 자속밀도방향, 중지 - 유기기전력의 방향

​

6. 패러데이 법칙에 대한 설명으로 가장 적합한 것은 ? ④

  ① 전자유도에 의해 회로에 발생되는 기전력은 자속 쇄교수의 시간에 대한 증가율에 비례한다.

  ② 전자유도에 의해 회로에 발생되는 기전력은 자속의 변화를 방해하는 반대방향으로 기전력이 유도된다.

  ③ #정전유도 에 의해 회로에 발생하는 기자력은 자속의 변화 방향으로 유도된다.

  ④ 전자유도에 의해 회로에 발생하는 기전력은 자속 쇄교수의 시간에 대한 감쇠율에 비례한다.

[해설] #패러데이 법칙 : 전자유도에 의해 회로에 발생하는 기전력은 자속 쇄교수의 시간에 대한 #감쇠율 에 비례한다.

​

7. #자속밀도 1[Wb/㎡]인 평등자계 중에서 길이 50[㎝]의 직선도체가 자계에 수직방향으로 속도 1[m/s]로 운동할 때의

     최대 유기기전력 [V]은 ? ②

   ① 0.1               ② 0.5                   ③ 1                        ④ 10

[해설] 유기기전력의 크기

     #유기기전력 e = Bℓv sinθ = 1 × 0.5 × 1 × sin 90° = 0.5 [V]

​

8. 10초 사이에 권선수 10회의 #코일 에 #자속 이 10[Wb]에서 20[Wb]로 변화하였다면 이 때 코일에 유기되는 #기전력 은

     몇 [V]인가 ? ③

    ① 0.1 [V]                ② 1.0 [V]                    ③ 10 [V]                  ④ 100 [V]

[해설] 유기기전력의 크기

가. 원자

  ① 원자는 중심에 원자핵(양성자+, 중성자로 구성)이 있고 그 주위에 일정한 궤도를 갖는 전자로 구성되어 있다.

  ② 원자핵의 양전기량과 전자의 음전기량은 같아서 원자는 전기적으로 중성을 띤다.

    ※ 물질의 양

나. 분자

  ▣ 물질의 성질을 가진 최소단위이다. 분자는 서로 다른 종류 또는 같은 종류의 원자가 결합하여 분자를 구성한다.

2. 전기의 발생

가. 자유전자의 이동

  ▣ 원자는 전기적으로 중성이다. 원자핵의 (+)전하량과 전자의 (-)전하량이 같기 때문이다. 그런데 외부의

       영향으로 빛이나 열 등의 영향으로 전자중 최외각 전자가 이동하게 하게 되는데 이를 자유 전자라고 하고

       한쪽 원자에서 다른 원자로 이동하게 되는데 이 때 전하량의 불평형이 생기는데 이와같은 현상으로

       전기가 발생하게 된다.

  ① 중성인 원자에 외부 열, 전기에너지가 가해지면 전자는 원자 궤도 밖으로 이탈한다.

  ② 전자가 이탈한 원자는 (-)가 줄어 전기적으로 (+)가 되고, 이탈한 전자는 다른 원자에 붙어 (-)가 늘어

       전기적으로 (-)가 된다.

  ③ 전기적으로 (+), (-)의 에너지를 가진 것을 전하(electric charge)라고 한다.

  ④ 양성자는 양전하(+)를 더 가졌고, 전자는 음전하(-)를 더 가졌다.

​

나. 전기력 (쿨룽의 힘)

  ▣ 두 전하 사이에 작용하는 힘

  ① 같은 전하 사이 : 반발력 (척력)

  ② 다른 전하 사이 : 흡인력 (인력)

​

다. 전하량 (전기량), Q

  ① 단위 : 쿨룽 (Coulomb : [C] )

  ② 양성자, 전자의 전하량

     1[C] = 6.24 × 10^18 e (e : 기본 전하량)

     1[C]은 6.24 × 10^18 개의 전자가 이동해서 만든 전기량

​

3. 전류, 전압, 기전력, 저항

  ▣ 전기는 물과 비교하면 이해하기 쉽다. 전지는 물탱크로 물의 흐름은 전류, 수압은 전압 수관은 전선으로 비교하면

       개념을 이해하기 쉽다.

      따라서 1초 동안에 1[C]의 전기량이 이동하였다면 전류의 세기는 1[A]가 된다.

  ② 전류의 방향 : 전자의 이동과 반대방향으로 (+)에서 (-)로 흐른다.

나. 전압 (Voltage)

  ① 정의 : 두 지점(전극)간의 전기적인 위치에너지 차이 (전위차)

                 기호 V, 단위 [V] (볼트)

  ② 크기

    ㉠ 1[V]는 단위전하 1[C]이 두 점 사이에서 이동하였을 때에 하는 일의 양이 1[J]일 때의 전위차이다.

    ㉡ 어떤 도체에 Q[C]의 전기량이 이동하여 W[J]의 일을 하였다면 이 때의 전압 [V]은 다음과 같다.​

     여기서, R : 저항[Ω], l : 길이 [m], A : 단면적 [㎡], ρ : 고유저항 [Ω·m]

​

【 출제 예상 문제 】

1. 대전에 의해서 물체가 가지는 전기 또는 전기량을 무엇이라 하는가 ? ②

   ① 전압          ② 전하            ③ 전류             ④ 저항

[해설] 전하 : 대전에 의해서 물체가 띠고 있는 전기

​

2. 다음 설명중 옳지 않은 것은 ? ②

   ① 양전하를 가진 물질은 음전하를 가진 물질 보다 전위가 높다.

   ② 전류의 흐름방향은 전자의 이동방향과 같다.

   ③ 전위차를 갖는 대전체에 도체를 연결하면 전류가 흐른다.

   ④ 전위차가 클수록 전류가 흐르기 쉽다.

[해설] 전류의 특성 : 전류는 전자의 이동과 반대방향인 (+)에서 (-)로 흐르고, 전자는 음극 (-)에서 양극(+)으로 흐른다.

​

3. 전자의 전기량[C]은 ? ③

4. 10[A]의 전류가 5분간 도선에 흘렸을 때 도선 단면을 지나는 전기량은 몇 [C]인가 ?

    ① 3,000[C]              ② 50[C]                ③ 2 [C]                  ④ 0.033 [C]

[해설] 전기량[Q] = Ⅰ· t = 10 × 300 = 3,000 [C]

​

5. 기전력 1[V]의 정의는 ? ①

   ① 1[C]의 전기량이 이동할 때 1[J]의 일을 하는 두 점간의 전위차

   ② 1[A]의 전류가 이동할 때 1[J]의 일을 하는 두 점간의 전위차

   ③ 2[C]의 전기량이 이동할 때 1[J]의 일을 하는 두 점간의 전위차

   ④ 2[A]의 전류가 이동할 때 1[J]의 일을 하는 두 점간의 전위차

[해설] V = W/Q [V], 여기서 V : 전압[V], W : 일[J]

​

6. 1[㎲] 동안에 1010 개의 전자가 이동할 때 흐르는 전류는 약 몇 [A]인가 ? ②

  ① 1.6 × 10^-6         ② 1.6 × 10-3             ③ 1.6             ④ 16

[해설]​

7. 다음중 [C/sec]와 같은 단위는 ? ③

    ① J             ② V              ③ A               ④ W

[해설] 전기량 Q = It 에서 I =Q[C] / t [sec] [A] ∴ 1[A] = 1 [C] / sec

​

8. 도체의 단면에 150[C]의 전하가 1분 동안 통과하였다면 이 도체에 흐른 전류의 크기는 몇 [A]인가 ?

   ① 2.5 [A]           ② 5.0 [A]             ③ 4,500 [A]             ④ 9,000 [A]

[해설] 전류 I = Q / t = 150 / 60 = 2.5 [A]

​

9. 10 [V]의 기전력으로 50 [C]의 전기량이 이동할 때 한 일은 몇 [J]인가 ? ③

   ① 250             ② 400                    ③ 500                  ④ 600

[해설] 1[V]는 1[C]이 흐를 때 1[J]의 일을 할 수 있게 하는 전압이므로

           W = V × C = 50 × 10 = 500 [J]