1. 테브난 정리
▣ 테브난 정리는 복잡한 회로를 간단하게 할 때 사용하는 것으로 하나의 전압원과
하나의 임피던스(저항)으로 표시하는 방법이다.
▣ 테브난 정리에 들어가기에 앞서 개방된 회로의 전압 관계에 대해 알아보자.

⊙ 위 회로도와 같이 내부저항이 1[Ω]일 때 부하저항이 커지면 전압전압이
부하저항에 많이 배분되다가 부하단자가 개방되어 저항이 무한대가 되면
전원 전압이 모두 단자에 걸리게 되며 내부저항에 걸리는 전압은 "0"이 된다.
가. 등가 전압원의 원리
▣ 특정 소자에 대한 회로를 분석할 때 그 소자의 전단에 복잡하게 회로와 전원이
얽혀 있을 때 전단의 회로를 하나의 전압원과 하나의 저항으로 단순화 시키는 것이
테브난의 정리이다.

⊙ 테브난 전압 : 개방단자 a, b에 발생하는 전압
⊙ 테브난 저항 : 전압원은 단락, 전류원의 개방시키고 a,b 단자에서 바라본 전압

⊙ 테브난 전압은 위와 같이 구하고, 테브난 저항은 다음과 같이 구한다.
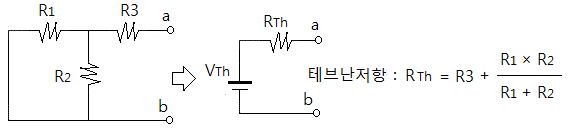
※ 테브난 저항은 전압원을 단락시키고 a, b 단자에서 바라본 합성저항을 말한다.
예제 : 다음 회로를 테브난의 정리에 의해 단순화 해 보자.

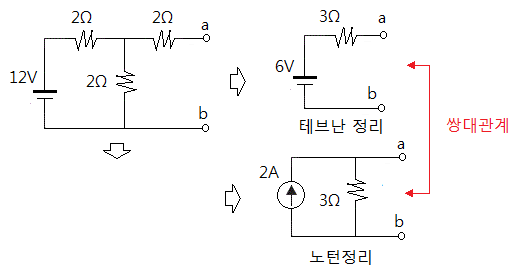
▣ 테브난의 정리와 노튼의 정리는 서로 쌍대관계에 있다. 상호간의 변환이 가능하다.
따라서 테브난과 노턴간의 변환 관계를 알아 보고 이 둘은 똑같은 회로를 전압과 저항을
직렬회로로 표시하느냐, 전류원과 저항을 병렬로 표현하느냐의 차이이다.

▣ 위와 같이 테브난의 정리와 노턴의 정리는 똑같은 회로를 다른 방식으로 표현한 것이며
서로 쌍대관계에 있어 변환이 가능하다.
나. 전원의 등가변환
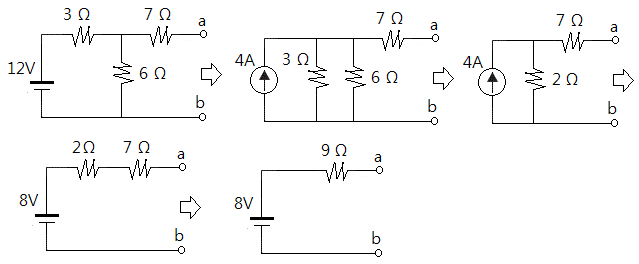
▣ 테브난의 정리의 전압원을 노턴의 정리의 전류원으로 바꿀 수 있다.
⊙ 위 테브난 정리 회로를 이용하여 노턴의 전류원으로 변환하여 보자.
예제 : 다음과 같은 회로가 있을 때 최대 전력 전송의 RL 값과 그 때의 전력전력(W)는 ?

2. 노턴의 정리 : 등가전류원의 원리
▣ 노턴의 정리는 복잡한 전류원과 회로를 하나의 전류원과 병렬의 임피던스(저항)로
단순화하는 것으로 등가전류원의 원리를 이용한 것이다.
⊙ 노턴전류 : a,b간 단자를 단락시켰을 때 a, b 단자간에 흐르는 전류를 말한다.
⊙ 노턴저항 : 개방단자 a, b 에서 바라 본 저항값을 말한다.
※ 전압원을 단락하고 전류원은 개방한 상태에서 a,b간의 합성저항을 구한다.

예제 : 다음 회로를 테브난 회로로 변환하여 보자.

▣ 노턴의 전류는 a, b단자를 단락시킨 후 a, b단자간에 흐르는 전류인데 a, b 단자간을
단락을 시키면 저항이 "0"이므로 모든 전류가 단락지점으로 흐르게 되어 전류원의
6[A]가 모두 흐르게 된다. 노턴의 저항은 a,b 단자에서 바라본 저항으로 전류원은 개방
하므로 전류원 쪽으로는 전류가 흐르지 않아 3[Ω]은 합성저항에 포함되지 않는다.
가. 전원 변환 : 테브난 ⇔ 노턴
▣ 테브난 회로와 노턴 회로는 쌍대 관계가 있어 상호 서로 등가변환할 수 있다.
⊙ 전원 등가변환은 오옴의 법칙에 따라 전압원 전압과 전류원 전류를 구하고
전압원에는 직렬저항을 연결하고 전류원에는 병렬저항을 연결한다.

예제 : 아래 회로에서 테브난을 이용하여 VR을 구하고 노튼을 이용하여 IR을 구하여라.

3. 밀만의 정리 - 테브난과 노튼과의 관계
▣ 테브난과 노튼과는 쌍대관계에 있다.
가. 테브난 정리

▣ 테브난 전압 : a, b 단자가 개방된 상태에서 a, b 단자간에 발생하는 전압
▣ 테브난 저항 : 전압원을 단락하고 a, b 단자에서 바라 본 전압
나. 노튼 정리

▣ 노튼 전류 : a, b 단자를 단락시겼을 때 a, b 단자에 흐르는 전류
▣ 노튼 저항 : a, b 단자에서 바라본 합성저항
다. 밀만의 정리
▣ 테브난의 정리와 노튼의 정리간에는 쌍대관계가 있다.
※ 저항은 그대로 두고 오옴의 법칙에 따라 전압원과 전류원을 변환한 다음
전압원에는 저항을 직렬로, 전류원에는 저항을 병렬로 연결한다.
4. 쌍대 회로
▣ 쌍대 회로 관계에 있는 것은 다음과 같다.
|
쌍대 관계
|
쌍대관계
|
||
|
전압 V
|
전류 I
|
임피던스 Z
|
어드미턴스 Y
|
|
저항 R
|
컨덕턴스 G
|
직렬
|
병렬
|
|
리액터 L
|
콘덴서 C
|
개방회로
|
폐회로
|
|
리액턴스 X
|
서셉턴스 B
|
테브난의 정리
|
노튼의 정리
|
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 테브난의 정리, 노튼의 정리, 밀만의 정리, 기출문제 풀이 (3) | 2022.01.03 |
|---|---|
| 테브난의 정리, 노튼의 정리, 밀만의 정리, 기출문제 풀이 (2) | 2022.01.03 |
| 회로망의 정리 - 선형회로망, 이상적인 전원, 중첩의 원리 (0) | 2022.01.01 |
| 인덕턴스와 벡터 궤적 - 기출 문제 풀이 (0) | 2021.12.31 |
| 인덕턴스와 벡터 궤적 - 2, 캠벨 브리지 (0) | 2021.12.30 |
