1. 캠벨 브릿지
▣ 캠벨 브리지는 '상호 인덕턴스 값'을 알아 내기 위한 회로입니다.

▣ 회로의 구성은 인덕턴스를 직렬 차동 접속하고 인덕턴스와 콘덴서를
병렬로 연결합니다.
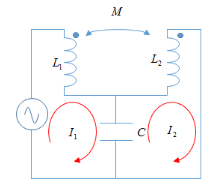
▣ 상호 인덕턴스 값을 구하기 위하여 왼쪽과 오른 쪽에 폐루프를 구성합니다.
오른 쪽 폐루프의 전압을 고려하여 보면 키르히호프의 전압법칙에 의하여
전체 전압의 합은 "0"이 됩니다.
즉 Vc + VL2 + VM = 0 이 됩니다.

따라서 I2 = 0 이 되기 위해서는 ω M = 1/ωC가 되어야 합니다.
위 식을 이용하여 상호 인덕턴스 M을 구할 수 있습니다.

따라서 위 식에 의하여 C값이나 ω 값을 조정하여 I2 = 0으로 한다면
그 때의 M값이 위 리액터 회로의 상호 리액턴스값이 됩니다.
2. 벡터의 궤적
▣ 벡터의 궤적은 각주파수 ω 즉, 주파수의 변화에 따라 임피던스 Z 또는 어드미턴스 Y가
어떻게 변화하는지 알아 보는 것이다.
가. R - L 직렬회로의 임피던스 궤적
▣ R - L 직렬 회로에서 임피던스 Z = R + jωL 이다. 이때 ω를 "0"에서 "∞"로 변화시킬 때
임피던스 변화를 그래프를 통해 알아 보자.

▣ R-L직렬 회로에서 ω를 0에서 ∞로 변화시키면 저항 R은 일정하고 ωL이 증가하면서
1사분면에서 직선으로 상승하게 된다.
나. R - L 직렬 회로의 어드미턴스 궤적
▣ R - L 직렬 회로에서 어드미턴스 Y=1/Z = 1/(R + jωL) 이다. 이때 ω 를 "0"에서 "∞"로
변화시킬 때 어드미턴스의 변화를 그래프를 통해 알아 보자.

▣ 어드미턴스를 계산하기 쉽게 공액 복소수를 분자, 분모에 곱하여 유리화해 보자.

▣ 어드미턴스 궤적에서는 ω = 0 일 때는 리액턴스 값이 "0"이 되므로 저항값만 남게 되고
저항값은 1/R 값이 된다. 만약 ωL = R 이 된다면 어드미턴스 값은 1/2R - j 1/2R값이
되고 ω = ∞가 되면 분모값이 ∞가 되므로 어드미턴스 값은 "0"이 된다.
▣ 종합하여 보면 R-L 직렬회로에서 어드미턴스값은 원점을 지나는 반원궤적을 그리며
4사분면에 나타나게 된다.
다. R - C 직렬회로의 임피던스 궤적
▣ R - C 직렬 회로에서 임피던스 Z = R -j 1/ωC 이다. 이때 ω를 "0"에서 "∞"로 변화시킬
때 임피던스 변화를 그래프를 통해 알아 보자.

▣ R-C회로에서 임피던스는 다음과 같다.

▣ R - C 직렬 회로에서 ω를 0에서 ∞로 변화시키면 저항 R은 일정하고 1/ωC이 - ∞에서
"0"으로 수렴하면서 직선으로 상승하게 된다.
라. R - C 직렬회로의 어드미턴스 궤적
▣ R - C 직렬 회로에서 어드미턴스 Y=1/Z = 1/(R - 1/jωC) 이다. 이때 ω 를 "0"에서
"∞"로 변화시킬 때 어드미턴스의 변화를 그래프를 통해 알아 보자.
▣ 어드미턴스를 계산하기 쉽게 공액 복소수를 분자, 분모에 곱하여 유리화해 보자.

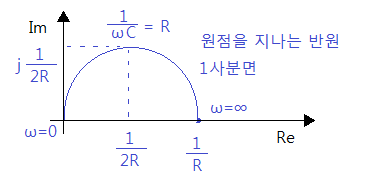
▣ 어드미턴스 궤적에서는 ω = 0 일 때는 리액턴스 값이 "∞"이 되므로 어드미턴스값은
"0"이 된다. 만약 1/ ωC = R 이 된다면 어드미턴스 값은 1/2R + j 1/2R값이 된다.
ω = ∞가 되면 리액턴스값이 "0"이 되므로 어드미턴스 값은 "1/R"이 된다.
▣ 종합하여 보면 R-C 직렬회로에서 어드미턴스값은 원점을 지나는 반원궤적을 그리며
1사분면에 나타나게 된다.
【 ω 의 변화에 따른 Z, Y 의 궤적 】
|
구 분
|
임피던스 (Z) 궤적
|
어드미턴스(Y) 궤적
|
|
|
직렬
|
R-L
|
직선 (1사분면)
|
반원 (4사분면)
|
|
R-C
|
직선 (1사분면)
|
반원(1사분면)
|
|
|
병렬
|
R-L
|
반원 (1사분면)
|
직선 (4사분면)
|
|
R-C
|
반원 (4사분면)
|
직선 (1사분면)
|
|
※ R-L-C 직렬회로에서는 어드미턴스 궤적이 원, 병렬회로에서는 임피던스 궤적이 원점을
지나는 원을 이룬다.
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 회로망의 정리 - 선형회로망, 이상적인 전원, 중첩의 원리 (0) | 2022.01.01 |
|---|---|
| 인덕턴스와 벡터 궤적 - 기출 문제 풀이 (0) | 2021.12.31 |
| 인덕턴스와 벡터 궤적 (0) | 2021.12.29 |
| 회로이론 - 교류전력 기출문제 풀이 (0) | 2021.12.28 |
| 교류 전력의 측정 (0) | 2021.12.26 |
