1. 기체
가. 보일(Boyle)의 법칙
▣ 보일의 법칙은 기체의 온도가 일정하면 기체의 압력과 부피는 반비례한다는 법칙으로, 영국의 자연철학자, 화학자이자
물리학자인 보일(R. Boyle, 1627-1691)이 1662년에 발견하였다.

▣ 비례식은 상수 K를 대입함으로써 등식으로 변형시킬 수 있다.
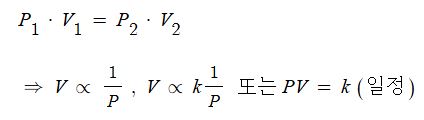
[예제] 1 atm에서 1,000ℓ 를 차지하는 기체가 등온의 조건 10 atm에서는 몇 ℓ 를 차지하겠는가 ?
[풀이] 1 : 10 = x : 1,000, x = 1,000 / 10 = 100 ℓ
나. 샤를(Charles)의 법칙
▣ 샤를의 법칙은 기체의 부피가 기체의 온도에 비례한다는 법칙으로, 프랑스의 과학자인 샤를 (J. Charles, 1746-1823)이
발견하였다.

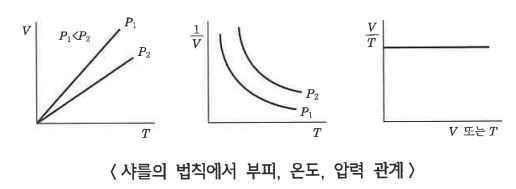
샤를의 법칙은 기체의 압력이 일정할 때 기체의 부피가 기체의 절대온도에 비례한다는 법칙이다.
이를 수식으로 나타내면 다음과 같다.

예제 : 15℃ 에서 3.5 ℓ를 차지하는 기체가 있다. 같은 압력 38 ℃에서는 몇 ℓ를 차지하는가 ?
[풀이] 기체의 부피는 절대온도에 비례한다는 샤를의 법칙을 적용하여 푼다.
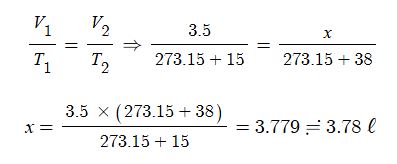
다. 보일-샤를 (Boyle-Charles)의 법칙
▣ 기체의 상태를 정의하기 위해서는 온도(T), 압력(P), 부피(V), 양 또는 몰 수(n) 네 가지 변수가 필요하다. 보일-샤를
법칙은 양(mole 수)이 일정할 때, 이상기체의 부피(V), 압력(P), 온도(T)의 관계를 나타내는 법칙을 말한다.
기체의 부피, 압력, 온도가 V1, P1, T1에서 V2, P2, T2으로 변하였을 때 다음 관계가 성립한다.


위 식에서 비례상수 k를 대입함으로써 다음과 같이 변형할 수 있다.

예제 : 273 ℃, 2 atm 에 있는 수소 1 ℓ 를 819 ℃, 압력 4 atm으로 하면 부피 (ℓ)는 얼마가 되겠는가 ?
[풀이] 보일 - 샤를의 법칙 비례식을 이용하여 푼다.

라. 아만톤 (Amanton's law)의 법칙
▣ 보일 - 샤를 (Boyle-Charles)의 법칙 중 등적의 조건에서 다음식을 유도할 수 있다.
이를 아만톤의 법칙이라 한다.

예제 : 27℃, 용기의 어떤 기체 압력이 10 atm이었다. 이 용기의 온도를 327 ℃로 올리면 용기내의 전체 압력은
몇 기압인가 ?
[풀이] 아만톤의 법칙에 따라 절대온도와 기압이 비례함을 이용하여 비례식으로 푼다.

마. 이상기체 상태 방정식 (출제빈도 높음) ★★★
① 아보가드로(Avogadro) 법칙
▣ 기체의 부피는 그 기체의 몰 (mol)수에 비례한다.
V ∝ n
위 식을 비례상수 k를 대입하여 다음과 같이 변형할 수 있다.
V = kn
보일(Boyle)의 법칙, 샤를의 법칙(Charles)의 법칙, 아보가드로 (Avogadro)의 법칙으로 부터 다음 식을 유도할 수 있다.

위 식에 비례상수에 기체 상수 R을 대입하면 다음과 같은 식이 성립하게 된다.

※ R (기체상수)
▣ 보일(Boyle)의 법칙과 샤를 (Charles)의 법칙 + 아보가드로 (Avogadro)의 법칙에서 유도

예제 : H2 (수소기체)가 0℃에서 부피는 9.65 ℓ 이며 압력은 2.5 atm 이다. 수소 기체의 몰 (mol) 수를 구하여라.

바. 기체의 분자량
▣ 이상기체 방정식을 이용하여 기체의 분자량을 구할 수 있다.

예제. 40℃, 190 ㎜Hg에서 1.6 ℓ의 기체 질량은 0.5 g 이다. 이 기체의 분자량을 구하여라.

사. 실제 기체 법칙
① 이상기체와 실제 기체
|
구 분
|
이상기체
|
실제기체
|
|
분자
|
질량은 있으나 부피는 없다.
|
질량과 부피 모두를 갖는다.
|
|
분자간의 힘
|
없다.
|
있다.
|
|
낮은 온도와 높은 압력
|
기체만으로 존재한다.
|
액체나 고체로 변한다.
|
|
- 273 ℃ 에서 상태
|
부피 = 0
|
고체
|
|
보일 - 샤를의 법칙
|
적확히 적용된다.
|
대략 맞는다.
|
② 반 데르 발스 (Van der Waals) 식 : 실제 기체에 적용되는 식으로는 여러가지가 있으나 반 데르 발스 (Van der Waals)의
식이 가장 널리 사용된다.

반 데르 발스 (Van der Waals) 상수 a와 b는 실험을 통해서 구할 수 있으며 다음과 같다.
|
기체
|
a ( atm · ℓ^2 / mol^2)
|
b (ℓ/mol)
|
|
He
Ne
Ar
Kr
Xe
H2
N2
O2
Cl2
CO2
CH4
NH3
H20
|
0.034
0.211
1.35
2.32
4.19
0.244
1.39
1.36
6.49
3.59
2.25
4.17
5.46
|
0.0237
0.0171
0.0322
0.0398
0.0511
0.0266
0.0391
0.0318
0.0562
0.0427
0.0428
0.0371
0.0305
|
예제 : 48℃에서 CO2 1몰의 체적이 1.32 ℓ 가 되는 압력을 이상기체 상태방정식과 반 데르 발스 상태방정식으로 계산하여
라.
◈ 이상기체 상태방정식 : PV = nRT

◈ 반 데르 발스 상태방정식
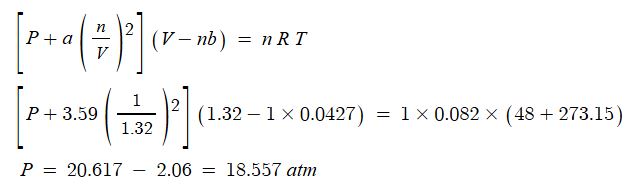
아. 돌턴 (Dalton)의 분압법칙
▣ 서로 반응하지 않는 혼합기체가 나타내는 전체 압력은 성분 기체들 각각의 압력(분압)을 합한 것과 같다는 것으로
다음과 같다.

위 식에서 PA 를 PT로 나누면 다음 식이 유도된다.

예제 : 용기에 산소, 질소, 아르곤이 채워져 있다. 이들의 몰분율은 각각 0.78, 0.21, 0.01 이며, 전체 압력이 2atm일 때
기체들의 부분 압력을 각각 구하여라.

자. 그레이엄 (Graham)의 법칙 : 그레이엄의 확산 속도 법칙(Graham's law of effusion)
▣ 기체들이 특정 용기에 갇힌 상태에서 용기의 작은 구멍을 통해 분출되는 속도(effusion rate)의 비는 각 기체의 질량비
의 제곱근에 반비례한다. 같은 온도에서 기체 분자의 운동에너지는 그 종류와는 관계없이 일정하므로 가벼운 분자는
상대적으로 빨리 움직이고, 무거운 분자는 상대적으로 느리게 운동한다. 기체 분자운동론의 관점에서 본다면,
용기 안에서 기체들은 끊임없이 직진운동을 하고 있다.
이러한 운동 중 기체가 용기의 구멍에 해당하는 부분의 표면에 부딪힐 때 기체는 용기에서 빠져나온다.
이렇게 용기에서 빠져나오는, 다시 말하면 단위 시간당 분출되는 기체분자의 수는 용기 내에 존재하는 특정 기체의
제곱평균근 속도 (root mean square (rms) velocity)에 비례한다.
▣ 기체의 분출속도를 온도와 압력이 동일한 조건하에서 비교하여 보면 분출속도가 기체 밀도의 제곱근에 반비례한다는
결과가 나타난다. 이 관계를 그레이엄 (Graham)의 법칙이라고 하며, 다음과 같은 식으로 나타낼 수 있다.

※ d, m : 크기 질량...
예제 : 어떤 기체가 프로판 기체 보다 약 1.6 배 더 빠른 속도로 확산하였다. 이 기체의 분자량을 계산 하시오.
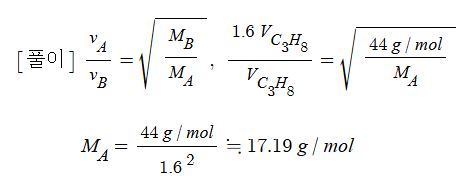
2. 액체 (Liquid)
▣ 액체는 모양은 변하나 부피는 일정하다. (진동, 회전 운동)
가. 액체의 일반 성질
① 압력을 가해도 분자간 거리가 별로 가까워지지 않으므로 압축이 잘 안된다.
② 일정량의 액체 부피는 일정하고 모양은 담긴 그릇의 모양에 따른다.
③ 액체 분자는 한 자리에 고정되어 있지 않고 유동한다.
나. 증기압력과 끓는 점
① 동적 평형 : 액체 분자가 증발되는 속도와 기체 분자가 액체로 응축되는 속도가 같은 상태
ex : 어떤 온도에서 물과 수증기가 동적 평형상태에 있다면, 수증기가 물로 되는 속도와 물이 수증기로 되는 속도가
같다.
② 증기압력 : 일정한 온도에서 증기 (기체)가 나타내는 압력
◈ 증기압력이 크다 = 휘발성이 크다 = 끓는 점이 낮다.
= 몰 증발열이 작다 = 분자간 인력이 약하다.
③ 끓는 점 : 액체의 증기압이 외부압력과 같아지는 온도로, 외부압력이 1기압일 때 끓는 점을 기준 끓는 점이라 하고,
따라서 외부 압력이 달라지면 끓는 점도 달라지며 외부 압력이 커지면 끓는 점이 높아진다.
<참고>
㉠ 증발 : 액체를 공기 중에 방치하여 가열하면 액체 표면의 분자 가운데 운동에너지가 큰 것은 분자간의 인력을 이겨
내어 표면에서 분자가 기체 상태로 튀어 나가는 현상
㉡ 증발열 : 액체 1 g 이 같은 온도에서 기체 1g 으로 되는데 필요한 열량 (물의 증발열은 539 cal/g)이다.
㉢ 증발과 끓음 : 액체의 표면에서만 기화가 일어나면 증발이고, 표면 뿐만 아니라 액체의 내부에서도 기화가 일어나면
끓음이라 한다.
예제. 물이 들어 있는 밀폐된 용기가 계속 가열되고 있다. 이 때 증기압력과 끓는 점의 변화는 어떻게 되는가 ?
[풀이] 밀폐되어 있는 용기를 압력밥솥으로 생각하면 끓는 점이 높아지면 쌀이 잘 익는다고 볼 때 온도가 올라 감에 따라
증기압력이 커지고 끓는 점도 높아진다.
3. 고체 (Solid)
▣ 고체는 그 모양과 부피가 일정하다. (진동운동)
가. 고체의 일반 성질
① 고정된 위치에서 진동운동만 한다.
② 유동성이 없고 일정한 모양과 부피를 가진다.
나. 융해와 녹는 점
① 융해열 : 녹는 점에서 고체 1g을 액체로 변화시키는데 필요한 열량
예 : 얼음의 융해열은 80 cal / g
② 몰 융해열 : 녹는 점에서 고체 1 몰을 액체로 변화시키는 데 필요한 열량
다. 고체의 승화
① 분자 사이의 인력이 약한 고체는 액체 상태를 거치지 않고 직접 기체 상태로 변한다.
예 : 나프탈렌, 아이오딘, 드라이아이스 등
라. 결정성 고체와 비결절성 고체
① 결정성 고체 : 입자들이 규칙적으로 배열되어 있는 고체로 녹는 점이 일정하다.
예 : 다이아몬드, 수정, 드라이아이스, 염화나트륨, 얼음
② 비결정성 고체 : 입자들이 불규칙하게 배열된 고체로 녹는 점이 일정하지 않다.
예 : 유리, 플라스틱, 아교, 엿, 아스팔트
[참고] 결정의 종류
㉠ 분자성 결정 : 결정을 구성하는 입자가 분자인 결정
예 : 드라이아이스, 나프탈렌, 얼음 등
㉡ 이온성 결정 : 정전기적 인력에 의한 결정
예 : NaCl, CaCl2, CaO, CsCl
㉢ 원자성 결정 : 결정을 구성하는 입자가 원자로서 공유결합에 의한 결정
예 : 다이아몬드, 흑연
㉣ 금속성 결정 : 금속 양이온과 자유전자 사이의 금속결합
예 : 알루미늄, 철 등의 금속
◈ 고체의 결합력 세기
원자성 결정 > 이온성 결정 > 금속성 결정 > 분자성 결정
◈ 고체의 분자 : 분자 사이의 간격이 극히 짧아서 분자와 분자 간의 인력이 크다.
#보일의법칙 #샤를의법칙 #아보가드로 #아만톤 #반데르발스 #돌턴 #그레이엄 #증기압력 #끓는점
'위험물 기능장 > 일반화학및유체역학' 카테고리의 다른 글
| 용액과 용해도 (0) | 2024.11.13 |
|---|---|
| 산과 염기 (2) | 2024.11.12 |
| 물질의 화학결합 (0) | 2024.11.09 |
| 원자의 구조와 원소의 주기율 (8) | 2024.11.07 |
| 물질의 상태와 변화 (5) | 2024.11.06 |
