1. 소화배관에 0.2 ㎥/s 의 유량이 흐르고 있다. 이 유량이 A, B의 분기관으로 나뉘어 흐르다가 다시 합쳐질 때 유속 [m/s]과
유량 [㎥/s]을 구하시오. [6점] ★★★★★
[조건]
① A, B 분기관의 마찰손실계수는 0.02 이다.
② A 분기관의 길이는 1,000 m, 직경은 200 ㎜ 이다.
③ B 분기관의 길이는 300 m, 직경은 150 ㎜ 이다.
가. 배관 A와 B의 유속 [m/s]을 각각 구하시오.
나. 배관 A와 B의 유량 [㎥/s]을 각각 구하시오.
[문제풀이]
▣ 두 배관이 나뉘어 흐르다가 합쳐지는 경우 두 배관에서의 마찰손실수두는 같다.
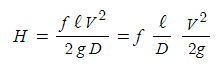
가. 배관 A와 B의 유속 [m/s]을 각각 구하시오.
⊙ A,B 관의 마찰손실수두가 같으므로 달시-웨버식으로 항등식을 만들 수 있다.
※ 다르시- 웨버 식에서 중력가속도 g, 마찰계수 f가 같으므로 이들은 약분한다.
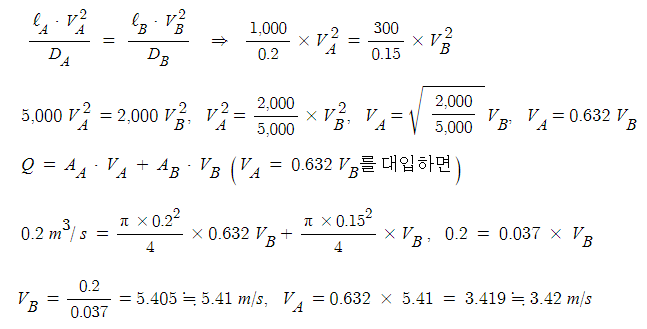
나. 배관 A와 B의 유량 [㎥/s]을 각각 구하시오.
Q = A · V [㎥/s] 식으로 계산한다.

2. 다음 그림과 같이 A지점으로 물이 유입되어 B지점으로 유출되고 있다. A ~ B 사이에 있는 3개의 분기관의 내경이
40 [㎜]라고 할 때 각 분기관으로 흐르는 유량을 계산하시오. [8점] ★★★★

[조건]
⊙ 배관의 마찰손실압력을 구하는 공식은 다음과 같다.

여기서, △P : 마찰손실압력 [MPa], Q : 유량 [ℓ/min], C : 조도, D : 배관경 [㎜], L : 배관길이 [m]
⊙ 유입점과 유출점에는 1,000 [ℓ/min]의 유량이 흐르고 있다.
⊙ 90° 엘보의 등가길이는 2 [m]이며, A와 B 두지점의 배관부속 마찰손실은 무시한다.
[문제풀이]
가. 전체 배관 유량
Q = Q1 + Q2 + Q3, Q : 전체관로 유량, Q1, Q2, Q3 : 병렬관로 유량
나. 하젠 - 윌리암스 공식

여기서, △P : 마찰손실압력 [Pa], Q : 유량 [ℓ/min], C : 관의 조도, D : 관의 내경 [㎜], L : 등가길이
① Q1 배관의 유량
병렬관로에서 문제 그림의 관로상 Q1 방향, Q2 방향 및 Q3 방향의 배관마찰손실은 동일하다.
△P1 = △P2 = △P3

그런데 위식에서 상수, C, D가 동일하므로 이를 생략하여 식을 정리하면 다음과 같다.
L1 × Q11.85 = L2 × Q21.85 = L3 × Q31.85
⊙ L1 : 15m + 20m + 15 m + (2m × 엘보 2개) = 54 m
⊙ L2 : 20 m
⊙ L3 : 5m + 20m + 5 m + (2m × 엘보 2개) = 34 m
54m × Q11.85 = 20m × Q21.85

△P1 = △P3 이므로 54m × Q11.85 = 34m × Q31.85

Q = Q1 + Q2 + Q3 (Q2 = 1.71 Q1, Q3 = 1.284 Q1 을 대입하면)
Q = Q1 + 1.71Q1 + 1.284 Q1 , 문제에서 Q = 1,000 ℓ/min 이라 하였으므로
1000 ℓ/min = Q1 + 1.71Q1 + 1.284 Q1, 1000 ℓ/min = 3.994 Q1

② Q2 배관유량
Q2 = 1.71 Q1 이므로 Q1에 위에서 구한 값 250.38 ℓ/min을 적용하면
Q2 = 1.71 × 250.38 ℓ/min = 428.149 ≒ 428.15 ℓ/min
③ Q3 배관유량
Q = Q1 + Q2 + Q3 에서 Q3 = Q - Q1 - Q2 이므로
Q3 = 1,000 ℓ/min - 250.38 ℓ/min - 428.15 ℓ/min = 321.47 ℓ/min
3. 다음 그림과 같이 1,500 ℓ/min의 유량이 Q1, Q2, Q3의 분기배관으로 나누어 흐르다가 다시 합쳐져 있다. 조건을 참조
하여 각 배관에 흐르는 유량 Q1, Q2, Q3 [ℓ/min]을 각각 구하시오. (단, 정답은 반올림하여 정수로 나타내시오) [10점]
★★★★
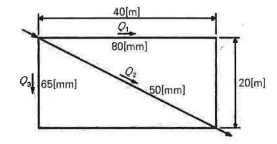
[조건]
① 각 분기관에서의 마찰손실은 10m로 모두 동일하다.
② 배관의 마찰손실은 다음의 하젠 - 윌리엄스의 식으로 산정한다.

여기서, △P : 마찰손실압력 [Pa], Q : 유량 [ℓ/min], C : 관의 조도, D : 관의 내경 [㎜], L : 등가길이
③ 배관의 조도는 모두 동일하다.
④ 비중량 γ = 9.8 kN/㎥ 이다.
[문제풀이]
▣ P = γH 이므로 △P = 9.8 × 10-3 ×10 = 0.098 MN/㎡ = 0.098 MPa
▣ 하젠-윌리엄스 공식을 유량 Q로 정리하면 다음과 같다.
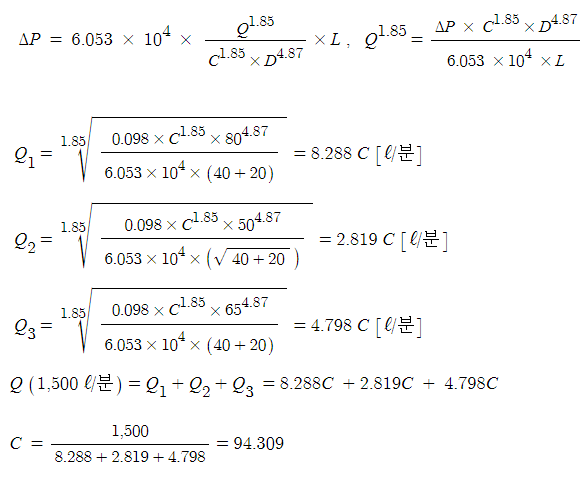
① Q1 배관의 유량
Q1 = 8.288 × 94.309 = 781.632 ≒ 782 [ℓ/min]
② Q2 배관의 유량
Q2 = 2.819 × 94.309 = 265.857 ≒ 266 [ℓ/min]
③ Q3 배관의 유량
Q3 = 4.798 × 94.309 = 452.494 ≒ 452 [ℓ/min]
4. 다음은 소화펌프의 흡입측 배관을 도시한 도면이다. 다음 각 물음에 답하시오. [10점] ★★★★

[조건]
① 펌프의 토출량은 180 [㎥/hr]이다.
② 소화펌프의 토출압력은 0.8 [Mpa] 이다.
③ 흡입배관상의 관부속품(엘보 등)의 직관 상당길이는 10 [m]이다.
④ 소화수의 증기압은 0.00238 [MPa], 대기압은 1 [atm]이다.
⑤ 배관의 압력손실은 아래의 하젠 - 윌리암스식으로 계산한다. (단, 속도수두는 무시한다.)

여기서, △H : 마찰손실압력 [mH2O], Q : 유량 [ℓ/min], C : 관의 조도 (100), D : 관의 내경 [㎜], L : 등가길이
⑥ 유효흡입양정의 기준점은 A로 한다.
가. 흡입배관에서의 마찰손실수두 [mH2O)를 구하시오. (단, 답은 소수점 넷째자리에서 반올림하여 셋째자리까지
구하시오.)
나. 유효흡입양정 (NPSHav)를 구하시오.
다. 필요흡입양정 (NPSHre)이 7 [mH2O)일 때 정상적인 흡입 운전가능여부를 판단하고 그 근거를 쓰시오.
라. 유효흡입양정과 필요흡입양정의 개념을 쓰고 NPSHav와 NPSHre의 관계를 그래프로 설명하시오.
[문제풀이]
가. 흡입배관에서의 마찰손실수두 [mH2O)를 구하시오. (단, 답은 소수점 넷째자리에서 반올림하여 셋째자리까지
구하시오.)
⊙ L (배관길이) : 12m + 4m + 4m + 0.5m +10m = 30.5m
⊙ Q (유량) : 180 ㎥/hr = 180 ㎥ × 103 [ℓ/㎥] × 1 hr/ 60 min = 3,000 ℓ/min

나. 유효흡입양정 (NPSHav)를 구하시오.
▣ 유효흡입양정 = 대기압 + 낙차 - 마찰손실압 - 증기압
NPSHav = Ha + Hh - Hf - Hv
⊙ Ha (대기압 환산수두) : 1 × 10.332 = 10.332 m
⊙ Hh (낙차) : 4 - 0.5 = 3.5 m
⊙ Hf (마찰손실수두) : 가. 에서 구한 2.519 m
⊙ Hv (증기압) : 0.00238 / 0.101325 × 10.332 = 0.242 m
∴ NPSHav = 10.332 + 3.5 - 2.519 - 0.242 = 11.071 ≒ 11.07 mH2O
다. 필요흡입양정 (NPSHre)이 7 [mH2O)일 때 정상적인 흡입 운전가능여부를 판단하고 그 근거를 쓰시오.
▣ 공동현상이 발생하지 않음 (정상흡입 가능 조건) : NPSHav > NPSHre
11.07 mH2O > 7 mH2O 이므로 정상적인 흡입 운전 가능
라. 유효흡입양정과 필요흡입양정의 개념을 쓰고 NPSHav와 NPSHre의 관계를 그래프로 설명하시오.
① NPSHav (유효흡입양정) : 펌프의 설치조건에 따라 결정되는 펌프로 가해지는 흡입측 으로 부터의 양정
② NPSHre (필요흡입양정) : 펌프 기동에 필요한 흡입측 압력을 말하며 펌프 회전에 의해 만들 수 있는 펌프의 내부 진공
도에 의해 결정
③ NPSHav와 NPSHre 의 관계 그래프

5. 다음 그림과 조건을 참조하여 각 물음에 답하시오. [5점] ★★★★

[조건]
① 대기압은 0.1 MPa 이다.
② 물의 온도는 20 ℃ 이고, 포화수증기압은 2.3 kPa이다.
③ 물의 비중량은 9.8 kN/㎥ 이다.
④ 배관 내 마찰손실수두는 0.3 m 이다.
가. 유효흡입양정 (NPSHav) [m]를 구하시오.
나. 필요흡입양정 (NPSHre)그래프를 보고 펌프의 사용가능여부와 그 이유를 설명하시오.
[문제풀이]
가. 유효흡입양정 (NPSHav) [m]를 구하시오.
▣ 유효흡입양정 (NPSHav)
NPSHav : Ha + Hh - Hf - Hv
여기서, NPSHav : 유효흡입양정 [m], Ha : 대기압 환산수두 [m]
Hh : 낙차압력환산수두[m] (흡입 : -, 압입 : +)
Hf : 흡입측 마찰손실 압력수두 [m]
Hv : 포화증기압 환산수두 [m]
P = γH 에서 H = P / γ
⊙ Ha : 대기압 환산수두 [m] : 0.1MPa = 0.1/0.101325 × 101,325 = 100,000 Pa = 100,000 N/㎡
H = 100,000 [N/㎡] / 9,800 [N/㎥] = 10.20 m
⊙ Hh : 낙차압력환산수두[m] (흡입 : -, 압입 : +) : 5 m
⊙ Hf : 흡입측 마찰손실 압력수두 [m] : 0.3 m
⊙ Hv : 포화증기압 환산수두 [m] : 2.35 kPa / 101.325 × 101,325 = 2,350 Pa = 2,350 N/㎡
H = 2,350 N/㎡ / 9,800 [N/㎥] = 0.239 m
∴ NPSHav = 10.20 - 5 - 0.3 - 0.239 = 4.665 ≒ 4.67 m
나. 필요흡입양정 (NPSHre)그래프를 보고 펌프의 사용가능여부와 그 이유를 설명하시오.
⊙ 펌프 흡입양정 (NPSHre) 그래프에서 정격운전시 (100% 운전시) 필요흡입양정은 4m 이므로 4.67 m > 4 m : 정상적인
펌프 운전 가능
⊙ 필요흡입양정 (NPSHre) 그래프에서 과부하 운전시 (150% 운전시) 필요흡입양정은 5m 이므로 4.67m < 5m : 공동현상
이 발생하므로 정상적인 펌프 운전 불가능
∴ 정격운전시 (100% 운전시)에는 정상적인 펌프운전이 가능하나 과부하운전시 (150% 운전시)에는 공동현상이 발생하므
로 정상적인 펌프운전이 불가능하다.
6. 아래 그림은 펌프를 이용하여 옥내 소화전으로 물을 배출하는 개략도이다. 열교환이 없으며, 모든 손실을 무시할 때,
펌프의 수동력 [kW]을 계산하시오. (단, P1은 게이지압이고, 물의 밀도는 ρ = 998.2 [㎏/㎥], 중력가속도 g = 9.8 [m/s2],
대기압은 0.1[MPa], 전달계수 K = 1.1, 효율 η = 75 [%] 이다.) [8점]

[문제풀이]
▣ 펌프의 수동력
P = γHQ
여기서, P : 수동력 [W], γ : 물의 비중량 [N/㎥], Q : 토출량 (유량) [㎥/s], H : 전양정 [m]
▣ 베르누이 방정식

여기서, H : 전수두 (전양정) [m], P1, P2 : 압력 [Pa = N/㎡], γ : 물의 비중량 [N/㎥], V1, V2 : 유속 [m/s]
g : 중력 가속도 (9.8 [m/s2), Z1, Z2 : 위치수두 [m], △H : 마찰손실수두 [m]
▣ 비중량
γ = ρ · g
여기서, γ : 물의 비중량 [N/㎥], ρ : 밀도 (㎏/㎥, N·s2/m4), g : 중력 가속도 (9.8 [m/s2)
▣ 유량

여기서, Q : 유량 [㎥/s], A : 배관의 단면적 [㎡] = π/4·d2 [㎡], V : 유속 [m/s], d : 내경 (안지름) [m]
① Q 유량 산정

② H 전양정 = 압력수두 + 속도수두 + 위치수두
⊙ 비중량 γ = ρ · g = 998.2 [㎏/㎥] × 9.8 [m/s2] = 9,782.36 N/㎥

∴ 수동력 P = γHQ = 9,782.36 × 0.035 × 20.83 = 7,131.829W = 7.13 kW
7. 원심펌프가 3,600rpm의 회전수로 회전하고 있다. 전양정이 120 m, 유량은 1,228 ㎥/min, 비속도가 200 ~ 260 rpm ·
m0.75 / min0.5 의 범위의 펌프로 설정하고자 할 때 몇 단의 펌프가 되는지 구하시오. [5점] ★★★
[문제풀이]
▣ 비교 회전도 (비속도)

여기서, Ns : 비교회전도 (비속도) [rpm · m0.75 / min 0.5]
N : 회전수
H : 양정 [m]
n : 단수
① 비교회전수 Ns = 200 [rpm · m0.75 / min 0.5] 일 경우 (최소단수)

② 비교회전수 Ns = 260 [rpm · m0.75 / min 0.5] 일 경우 (최대단수)

∴ 단수가 2.218 단 ~ 3.147 단이므로 3단 펌프를 선정한다.
#압력 #유효흡입양정 #필요흡입양정 #마찰손실압력 #병렬관로
'소방설비기사기계실기' 카테고리의 다른 글
| 소방설비기사 기계 답답형 정리 (0) | 2024.08.26 |
|---|---|
| 가스계 소화설비 약제저장량 관련 공식 정리 (2) | 2024.07.13 |
| 포소화설비 기출문제풀이 - 2 (수정) (0) | 2024.07.11 |
| 스프링클러설비(간이) 기출문제풀이 - 10 , 배관 및 관부속품 (2) | 2024.07.09 |
| 스프링클러설비 기출문제풀이 9 - 소방기계 실기 (0) | 2024.07.08 |
