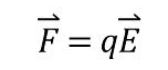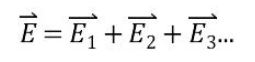아낌없이 주는 나무

가우스의 법칙은 독일의 수학자 칼 프레드리히 가우스가 1867년 발표한 전기력학의 기초라고 할 수 있다. 이 법칙은 대칭성을 가진 전하분포상에서 전기장을 구하는데 아주 유용하게 쓰인다.

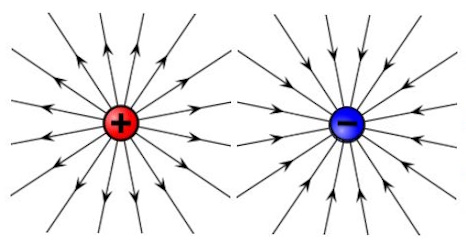
전기력의 세기를 구하거나 전기장을 정의할 수 있는 공식 중의 하나인 쿨룽의 법칙이 있는데 이 쿨룽의 법칙은 모든 전기력을 구하는데는 한계가 있다. 쿨룽의 법칙은 '점전하 (point charge)를 가정하여 전기력을 구한다. 그런데 현실에서는 전기력이 점전하 뿐만 아니라 다양한 형태로 존재하고 이런 전기력을 구하는데에는 쿨룽의 법칙은 한계가 있다.

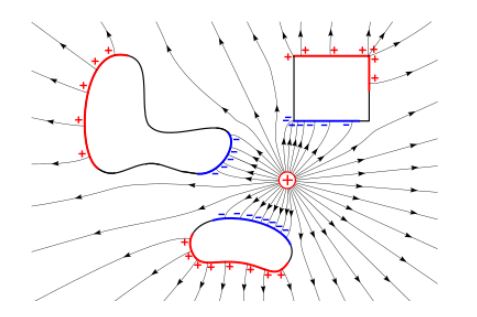
일상에서는 위 그림 처럼 원형, 육각형, 사각형 등의 다양한 형태의 크기와 넓이를 가진 물건들이 많은데 크기를 고려하지 않는 쿨룽의 법칙으로는 이들의 전기력, 전기장을 계산하기가 힘들다. 이런 것들의 전기장을 구하려면 적분을 통해 이 물체의 전하분포를 엄청 잘게 잘라서 점전하급으로 잘게 나눈 후, 그 점전하들의 전기장을 합하여 계산할 수 있지만 전기장은 크기 뿐만 아니라 방향도 가지고 있어 계산이 매우 어렵게 된다.

위 식과 같이 매우 복잡한 계산을 해야 한다.

​

위와 같은 복잡한 계산 식을 사용하지 않고 전기장을 쉽게 구하기 위해 나온 계산식이 바로 '가우스의 법칙'이다. 그러나 가우스의 법칙도 선, 구, 면 처럼 전하의 분포가 대칭성을 가지는 경우에만 적용이 가능하지만 적어도 대칭성을 가진 전하분포일 때 전하를 구하는 방식은 가우스 법칙하나만으로 아주 간단하게 구할 수 있다.

​

가우스의 법칙은 무엇일까 ?

위 식은 가우스의 법칙을 나타낸 식이다.

이를 우리말로 표현을 하면 '임의의 폐곡면 (가우스면)을 통과하는 전기선속은 폐곡면내의 총 전하량에 비례한다'라고 할 수 있다. 이말은 어떤 의미일까 ? 상세히 알아 보자.

​

1. 전기선속 (electric flux)이란 ?

위 그림처럼 넓이가 A인 사각형 단면을 전기력선이 통과하고 있다고 가정해 보자. 전기력선의 밀도는 전기장의 크기에 따라 달라지는데 그렇다면 단면 A를 지나가는 전기력선의 갯수는 E × A 에 비례한다. 이것을 '전기장 다발' 혹은 '전기력선속'으로 부르며 electric flux 라고 하며 기호로는 ф 대문자 파이 (phi)로 나타낸다.

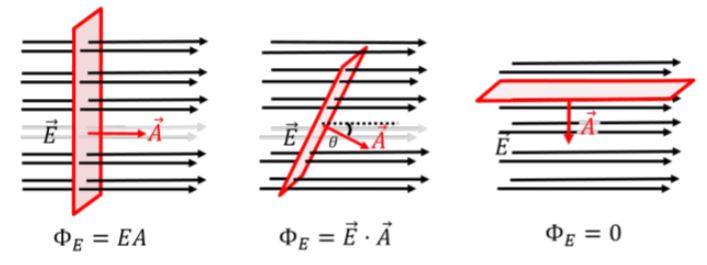
그런데 위 그림에서 처럼 맨 앞 그림은 단면이 전기력선속과 수직으로 되어 있지만 경우에 따라서는 가운데 그림처럼 비스듬하게 놓여 있을 수도 있고 극단적으로 면이 수평으로 누워있을 수도 있다. 그렇다면 전기력선과 단면이 수직인 경우에 비해 전기력선이 단면에 통과하는 경우에 통과하는 양이 적어지므로 전기선속 Φ = EA cos θ 로 구하게 된다. 즉, 전기선속은 단면과 전기력선속이 수직일 때 제일 크고, 수평일 때 가장 작다.

그렇다면, 단면이 아닌 닫힌 곡면, 즉, 폐곡면의 경우를 살펴보자. 위 그림과 같이 구체 모양인 곡면의 정중앙에 양전하 q가 있다고 하자. 이 양전하 q가 뿜어내는 전기장에 의해 구체 표면으로 빠져 나가는 전기선속을 구하려면 곡면을 잘게 나누어서 잘게 나눈 면의 전기장을 구한 다음 각각의 전기장을 합하면 될 것이다. 이를 수식으로 나타내면 다음과 같다.

위와 같이 전기장 (방향을 가진 벡터값)과 면적벡터를 폐곡면에서 모두 적분을 하면 되지만 이는 계산하기 매우 까다롭다.

​

2. 점전하에 대한 가우스 법칙

그렇다면 점전하 q가 반지름이 R(=r)인 구의 중심에 잇다고 가정을 하자. 쿨룽의 법칙에 의하면 전기장의 크기는 다음과 같이 구할 수 있다.

구의 표면적은 4πr2 이므로 가우스면 (폐곡면)을 일컫는 dA = 4πr2 이 된다. 이를 식으로 표현하면 다음과 같다.

여기서 알수 있는 중요한 사실은 구체의 반지름 r이 어떻게 되든 전기선속의 값에는 아무런 영향을 주지 않는다는 것이다. 결국, 전기선속의 값은 입실론 (ε)의 값도 정해져 있으므로 가우스면 내부의 '총 전하량'에만 영향을 받는다는 것을 알 수 있다.

만약에 점전하 하나가 위 그림의 S1이라는 폐곡면의 중심에 있는데 폐곡면이 만약 구체 형태가 아닌 S2, S3와 같이 찌그러진 곡면이라고 하면 이 때 폐곡면에서 나가는 전기력선의 수가 달라질까 ? 위의 오른쪽 그림만 보아도 그렇지 않다는 것을 쉽게 알 수 있다. 결국 가우스면 이기만 하면 곡면의 반지름과는 상관없이 총 전하량에 의해서만 전기력선속이 정해진다는 것을 그림으로 알 수 있다.

결국 폐곡면이기만 하면, '임의의 폐곡면(가우스면)을 통과하는 전기선속은 폐곡면 내의 총전하량에 비례한다'는 법칙이 성립하는데 이것이 바로 전자기학에서 말하는 가우스 법칙 (Gauss's law)이다.

​

※ 주의

⊙ 가우스 법칙에서 가장 오른 쪽 Q는 가우스면 내부의 알짜 전하량을 의미하나 E는 가우스면 내외부의 전체 전기장임을

     염두에 두어야 한다.

⊙ 전기선속이 "0"이면 전기장도 "0"이다. 아니다.

     가우스 법칙은 전기선속이 폐곡면 내부의 알짜 전하량에 비례한다는 것이지, 전기장이 폐곡면 내부의 알짜 전하량에

     비례한다는 것이 아니다.

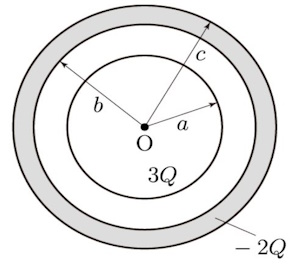
가우스 법칙은 대칭성을 가진 전하 분포에 대한 전기장을 계산할 때 아주 유용하게 쓰이는데 이를 구하려면 가우스 법칙만으로는 계산이 어렵고 대칭성을 이루는 형태 (구, 원통, 평면 등)에 대한 '표면전하 밀도'를 알고 있어야 계산이 가능하다.

​

#가우스 #폐곡면 #전기력선속 #전기력선 #점전하 #쿨룽 #알짜 #전기장

1. 전기장이란 ?

전기장 (Electric field)은 '어느 하나의 전하가 전기적인 힘을 미치는 공간'이라고 할 수 있다. 다시 말하면 어느 공간에 하나의 전하를 놓으면 주위에 있는 다른 전하에게 영향을 미치는 성질이라 할 수 있다. 여기서 '장(field)'에는 전기장 뿐만 아니라 중력장, 자기장 등도 있는데 예를 들어 자석에 쇠구슬을 서서히 다가가게 하면, 어느 일정한 거리에 도달하는 순간 자석이 쇠구슬을 끌어 당기면서 자석에 붙게 된다. 이는 자석이 가진 힘이 미치는 공간, 즉 장(field)에 쇠구슬이 진입했기에 쇠구슬이 자석의 힘의 영향을 받게 된 것이다.

이 예를 통해 '장(field)'이란 비접촉력을 설명할 때 사용하는 용어라는 것을 알 수 있다.

전기장도 마찬가지로 하나의 전하의 힘이 이웃한 전하에게 영향을 미치는 영역을 말한다.

위 그림에서 원전하 Q의 근처에 임의의 시험전하 q가 들어 왔다고 가정을 해 보자.

Q와 q가 모두 양전하라면 Q와 q는 서로 척력을 발생시키며 반발할 것이다. 그러면 반발력이 Q와 q가 서로 맞닿아 있을 때만 발생하는가 ? 그건 아니다.

전기장 (Electric field)이라는 성질은 공간적으로 떨어져 있는 곳에도 영향을 미친다는 의미가 포함되어 있으므로, Q와 q는 일정한 거리에 접근하는 순간 Q의 전기장에 의해 서로 닿지도 않았는데 반발력이 발생하게 된다. 만약에 Q는 양전하이고 q는 음전하라면 Q의 전기장내에 q가 들어서면 서로 끌어 당기는 인력이 발생할 것이다.

이러한 전기장을 식으로 표현할 때 E (전계의 세기)로 표현하며, 전기장을 알고 있을 때 전기력을 구하는 식은 다음과 같다.

이와 같이 전기장을 알게 되면 전기장 내에 있는 전하가 받는 힘의 크기와 방향도 알 수 있게 된다. 다시 말하면 전기장 (전계의 세기) E는 시험전하 q가 Q의 전기장 내에서 전기력을 받는 세기라고 할 수 있다.

Q와 q가 점전하라고 한다면 전기력은 쿨룽의 법칙에 의하여 구할 수 있고, 이 식에서 전기장 (전계의 세기)을 구하는 식을 유도할 수 있다. 위 식에서 결국 전기장을 구하는 식은 쿨룽의 법칙, 전기력을 구하는 식에서 시험전하의 전하량 q를 빼면 된다.

​

위 식에서 이 전기장에 대하여 하나 덧붙이면, 전기장이 균일하게 분포되어 있다고 가정하면 전하량이 q이고 질량이 m인 입자를 균일한 전기장 E 내에 놓았을 때의 입자가속도를 구할 수 있게 된다.

※ 전기력 F는 단지, 힘의 종류 중에 하나이므로 뉴턴의 운동법칙 F = ma 의 식을 적용할 수 있다.

위와 같이 F = ma 를 이용하여 균일한 전기장 E 내에 위치한 전하 q, 질량 m인 입자의 입자 가속도를 구하는 방정식을 유도해 낼 수 있다. (단, 균일한 전기장일 때 입자에 작용하는 전기장이 일정하여 등가속도 운동임을 특정할 수 있다)

​

2. 전기력선이란 ?

​

전기력선 (Electric field lines)은 '전기장을 눈에 보이게 선으로 그려 놓은 것'이라 할 수

있다. 전기장을 형성하는 전기력선의 벡터를 선으로 이어 놓은 것이라 할 수 있다.

양전하, 음전하이냐를 떠나서 모든 전하는 자신만의 전기장을 갖게 되는데, 이 전기장은 눈에 보이지 않으므로 전기장이 미치는 범위와 형태를 선으로 표현하면 이해하기가 쉽게 된다. 가장 기본적인 전기력선은 위 그림처럼 양전하와 음전하의 전기장을 표현하는 것인데 음전하는 화살표가 안쪽으로 양전하는 화살표가 바깥쪽으로 향하게 된다.

이 때 전기력선의 규칙은 다음과 같다.

  ⊙ 전기장 벡터 E는 각 점에서 전기력선의 접선방향이다.

  ⊙ 전기력선은 양전하에서 나와서 음전하로 들어간다.

  ⊙ 전기력선은 서로 교차하지 않는다.

이러한 규칙에 따라 전기력선은 위 그림과 같이 다양한 형태로 나타난다. 전하 하나만 독립적으로 존재하거나, 같은 극성을 같는 전하가 이웃할 때, 다른 극성을 갖는 전하가 이웃할 때 등 전기력선이 나타는 모양을 각각 다르게 된다.

전기력선은 단순히 방향만을 알려 줄 뿐만 아니라 전기력선이 어떻게 분포되어 있느냐에 따라 전기장의 세기도 가늠할 수 있다. 전기력선이 듬성듬성 분포한 곳은 상대적으로 전기장이 약한 곳이며, 전기력선이 촘촘히 분포한 곳은 전기장이 상대적으로 강한 곳이다.

​

그런데 지금까지는 전하가 각각 하나씩 존재하는 경우를 가정했는데 현실 세계에서는 전하가 하나의 공간에 무수히 많이 존재하게 된다. 한 공간에 전하가 무수히 많이 존재하게 되면 각 전하가 가진 전기장이 서로 중첩될 수 있는데 이럴 경우 특정지점의 전기장 E는 그 주변에 존재하는 무수한 전하들의 전기장들의 벡터합으로 표현할 수 있다. 이를 중첩의 원리라고 하며 식으로 표현하면 다음과 같다.

#전기장 #전계의세기 #전기력선 #자기장 #전하