1. 포물선 운동
포물선 운동에 대하여 알아 보자.
포물선 운동을 분석하기 위해서는 먼저 벡터운동의 합성에 대해 알아야 한다.
벡터는 수평성분 cos 성분과 수직성분 sin 성분으로 구성되어 있다.
포물선 운동에서도 이들 벡터성분을 구분하여 합성을 하면 이해하기 쉽다.
다음 그림을 보면서 포물선 운동에 대하여 알아 보자.

어떤 물체를 지면에서 30°의 방향으로 40m/s의 속도로 던졌다고 하고 이 때 공기저항은 없다고 가정을 해 보자. 공기저항이 없기 때문에 이 물체는 오로지 중력의 영향만 받는다.
초기 속도 Vo = 40 m/s 이다. 이는 벡터 성분이므로 높이 방향으로 움직이는 연직 상향 운동 성분과 거리, 시간 방향인 등속직선운동 성분으로 구분할 수 있다.
수직 운동 성분인 연직 상향 운동 성분은 초기 속도에 sin θ 를 곱해 주어 Vo sinθ 로 나타낼 수 있고 40 sin 30° = 20 m/s가 된다. 마찬가지로 수평 운동 성분인 등속직선운동은 초기 속도에 cos θ를 곱해 주어 Vo cos θ 로 나타낼 수 있고 40 cos 30° = 20 √3 m/s가 된다.
포물선 운동을 분석할 때는 최고점 높이에 도달하는 시간을 먼저 구하면 다른 것 들을 쉽게 구할 수 있게 된다. 최고점 높이에 도달하는 시간을 구해 보면 다음과 같다.

또한 물체가 공중에 체공하는 시간은 최고점에 도달하는 시간의 2배이므로

다음은 최고점 도달 높이에 대하여 알아 보자. 도달 높이는 평균속도 × 시간으로 구할 수 있다. 그런데 초기 속도를 V 라고 한다면 마지막 속도는 "0"이 된다. 따라서 평균속도는 V/2로 나타낼 수 있다. 이를 식으로 나타내면 다음과 같다.

수평 도달 거리도 같은 방식으로 계산할 수 있다. 거리 S = 속도 × 시간이다.

수평 운동은 등속 직선운동이라고 가정하였으므로 속도 V = Vo cos θ [m/s]가 된다.
그러므로 거리 S = V · t 로 나타낼 수 있다.

가속도, 속력, 높이와 관련된 식을 정리하면 다음과 같다.

2. 등가속도 직선 운동
등가속도 운동은 시간이 변화함에도 가속도는 일정한 운동을 말한다.
등가속도 직선운동을 통하여 가속도와 속도 그리고 시간과의 관계에 대해 알아보자.

위 그림 (a)에서 보는 바와 같이 등가속도 직선운동은 시간에 관계없이 가속도가 일정한 운동의 상태를 말한다. 그림 (b)에서는 시간과 속도와의 관계를 보여준다. 등가속도 직선운동의 경우에 시간의 변화에 대해 속도의 변화도 일정한 경우에 해당한다. 따라서 속도의 변화율 즉, 속도변화 직선의 기울기가 가속도가 된다. 그림 (c)에서는 시간과 거리와의 관계를 나타내는데 등가속도 직선운동에서는 시간의 변화에 따라 이동 거리는 기하급수적으로 변화함을 보여 주고 있다. 그림 (b)에서 속도 변화를 식으로 나타내면 다음과 같다.

그림 (b)에서 이동 거리는 직선 아래의 면적으로 나타내는데 그 면적은 □ 면적과 △ 면적의 합이 된다.

이 공식은 시간이 주어지지 않았을 때 이동 거리를 구할 때 사용하는 공식이다.
이 식의 유도과정을 알아 보면 다음과 같다.

이는 뉴톤의 운동방정식으로도 유도할 수 있다.

위 그림은 어떤 물체에 F라는 힘을 가하여 S 만큼 이동하였고 속도는 당초 V1에서 V2로 변화한 것을 보여 주고 있다. 이를 통하여 위 식을 유도해 보자.
위 그림에서 행하여 진 일의 양은 W = F · S가 되며 다음과 같이 유도된다.

【 등가속도 직선운동】
다음의 그래프를 이용하여 등가속도 직선운동 관련식으로 위 식을 유도해 보자.

앞서 등가속도 직선운동에서 다음 식이 성립함을 보았다.
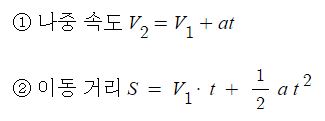
또한 가속도 정의에 의하여 다음 식이 성립함을 알 수 있다.

위 그래프이 기울기는 가속도를 의미하는데, 기울기 = Y/X = 속도/시간 = 가속도이고
직선 아래의 면적은 이동거리를 나타내는데
면적 = X × Y = 속도 × 시간 = 변위 (이동거리)
직선 아래 면적을 구해 보면

위와같은 식이 성립된다.
#등가속도 #운동법칙 #유도식 #뉴톤 #가속도 #시간 #속도 #변위 #포물선 #중력
'소방설비기사 (기계) > 기초물리' 카테고리의 다른 글
| 몰(mol), 몰질량, 몰부피, 입자수 사이의 관계 (0) | 2024.08.08 |
|---|---|
| 분류에 의해 작용하는 힘 (0) | 2024.08.07 |
| 운동량과 충격량 (Momentum & Impulse) (0) | 2024.08.07 |
| 베르누이 방정식과 토리첼리 정리 (0) | 2024.08.07 |
| 뉴톤의 운동법칙 : 힘과 운동 (0) | 2024.08.07 |






































