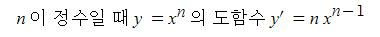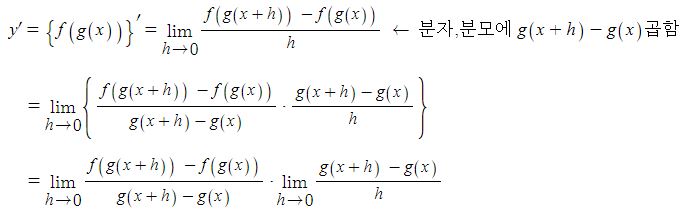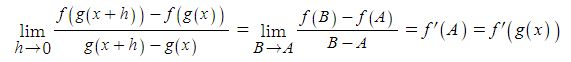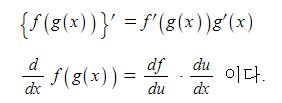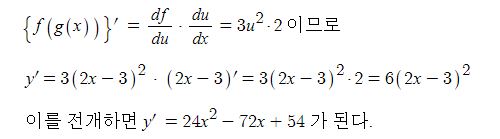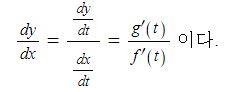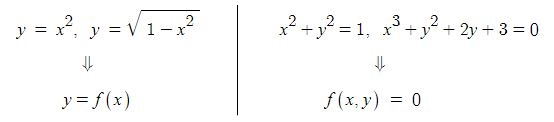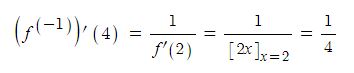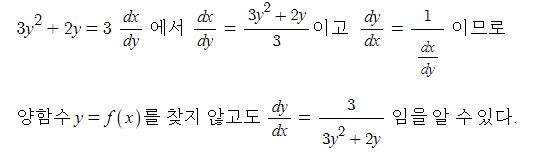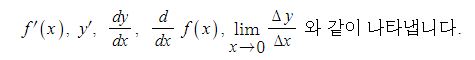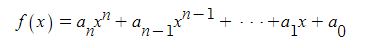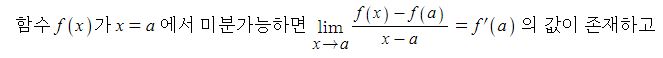아낌없이 주는 나무

삼각함수의 덧셈 또는 뺄셈을 곱셈으로 고치는 공식과 삼각함수의 극한을 이용하여 삼각함수의 도함수를, 지수함수와

로그함수의 극한을 이용하여 지수함수와 로그함수의 도함수를 구하는 방법을 알아 보자. 또한 이계도함수의 정의와

이계도함수의 계산법도 알아 보자.

​

1. 삼각함수의 도함수

삼각함수의 도함수를 구하려면 임의의 점에서의 미분계수를 구하면 되는데 삼각함수의 극한을 구할 수 있다.​

가. 삼각함수 y = sin x, y = cos x, y = tan x 의 도함수는 도함수의 정의와 삼각함수의 극한, 삼각함수의 합 또는 차를

      곱으로 변환하는 공식을 이용하여 구할 수 있다.

① y = sin x 의 도함수​

따라서 (sin x)' = cos x 이다.

​

② y = cos x의 도함수​

따라서 (cos x)' = - sin x 이다.

​

③ y = tan x 의 도함수​

   따라서 (tan x)' = sec2 x 이다.

​

나. 삼각함수 y=cosec x, y = sec x, y = cot x 의 도함수도 바로 위에서 구한 세 삼각함수의 도함수와 몫의 미분법을

      적용하여 구할 수 있다.

① y = cosec x 의 도함수​

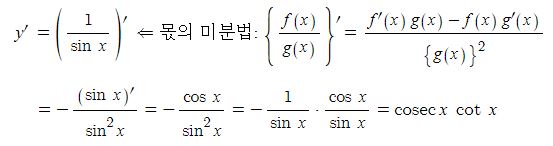
② y = sec x 의 도함수​

   따라서 (sec x)' = sec x · tan x 이다.

③ y = cot x 의 도함수  ​

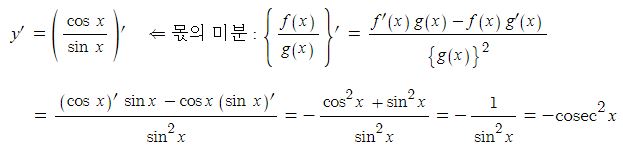
【 삼각함수의 도함수】​

2. 지수함수의 도함수

지수함수 y = e^x, y = a^x 의 도함수는 도함수의 정의와 지수함수의 극한을 이용하여 구할 수 있다.​

가. y = e^x 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 하면​

나. y = ax (a >0, a ≠ 1) 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 하면​

참고로 합성함수의 미분법을 이용하여 y = ex 의 도함수를 구할 수 있다.​

3. 로그함수의 도함수

로그함수 y = ln x, y = log ax (a >0, a ≠1)의 도함수는 도함수의 정의와 무리수 e의 정의에 의하여 구할 수 있다.​

가. 로그함수의 도함수

y = ln x 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 한다면

△y = ln (x+△x) - ln x 가 되므로 도함의 정의에 의해​

또한 로그의 성질 log ax = ln x / ln a (a >0, a≠1)를 이용하면 다음과 같이 y =log ax 의 도함수를 구할 수 있다.​

나. 절대값을 포함한 로그함수의 도함수

미분가능한 함수 f(x)에 대하여 f(x) > 0 또는 f(x) <0 인 경우에 ln lf(x)l 의 도함수를 구해 보자.

① f(x) > 0 일 때, lf(x)l = f(x)이므로 u = f (x)로 놓으면 y = ln u​

② f(x) < 0 일 때, lf(x)l = -f(x)이므로 u = -f (x)로 놓으면 y = ln u​​

【 로그함수의 도함수 】​

따라서 ①, ② 를 정리하여 보면​

4. 로그 미분법

가. 로그 미분법

밑과 지수에 모두 변수를 포함하는 지수형태의 함수나 복잡한 분수함수의 도함수를 구하기 위해서는 양변에 로그를

취한 후 합성함수의 미분법이나 음함수의 미분법을 적용하면 된다.

이런 방법을 로그미분법이라고 한다. 이때 로그의 진수가 양수이어야 하므로 로그를 취하기 전에 식의 양변에 절대값을

먼저 취한 다음 로그를 택해야 한다. 만약 이미 양변이 양수일 때는 절대값을 취하지 않아도 된다.​

몫의 미분법과 합성함수의 미분법을 적용하면 도함수를 구할 수 있지만 식이 매우 복잡하므로 로그를 취한 후 음합수

미분법을 이용하여 도함수를 구하는 것이 보다 빠르고 쉽다.

양변이 모두 양수이므로 식의 양변에 자연로그를 취하여 로그의 성질을 이용한다.​

즉, 함수 y = f(x) 에서 f(x)의 형태가 일반적인 미분법을 적용하기에 복잡한 형태라면 로그미분법을 이용해서

다음 순서에 따라 함수의 도함수를 구할 수 있다.

【 로그 미분법 】

복잡한 지수와 몫으로 표현된 함수는 로그미분법을 이용하여 도함수를 구할 수 있다.

① 양변에 절대값을 취한다. ⇒ ㅣyㅣ= l f(x)ㅣ

② 양변에 자연로그를 취한다. ⇒ ln ㅣyㅣ = ln l f(x)ㅣ​

나. y = xa 의 도함수 (단, a는 실수)

자연수 지수에서 부터 유리수 지수까지는 함수 y = x'의 도함수가 y'=r xr-1 이다.

이제 로그미분법을 이용하여 a가 임의의 실수일 때, 함수 y = xa의 도함수를 구해 보자.​

【 로그 미분법의 활용 】

가. 지수함수 y = ax (a > 0, a ≠ 1)의 도함수를 로그미분법을 이용하여 구해 보자.

      y = ax 의 양변에 자연로그를 취하면 ln y = ln ax = x ln a

      양변을 x에 대하여 미분하면​

   위 식은 지수함수를 미분해서 얻은 도함수와 그 결과가 일치한다.

나. 이번에는 y =af(x) 의 도함수 (a>0, a≠1)를 로그미분법을 이용하여 구해 보자.​

   이 또한 지수함수를 포함한 합성함수의 도함수와 그 결과가 일치한다.

​

5. 이계함수

함수 y = f(x) 의 도함수 f'(x)가 미분가능하면 f'(x)의 도함수는 다음과 같다.​

이 때, f'(x)의 도함수를 함수 f(x)의 이계 도함수라고 하고 기호로는 다음과 같이 나타낸다.​

즉, 이 이계도함수는 어떤 함수를 두번 미분한 함수이다.

일반적으로 자연수 n 에 대하여 함수 y = f(x)가 n번 미분가능한 함수일 때 y = f(x)를 n번

미분하여 얻은 함수를 y = f(x)의 n계도함수라고 하고 기호로는 다음과 같다.​

【 이계 도함수 】

함수 y = f(x)의 도함수 f'(x) 가 미분가능할 때, f'(x)의 도함수를 y = f(x)의 이계도함수라

하고 기호로는 다음과 같이 나타낸다.​

#삼각함수 #도함수 #미분 #미분계수 #지수함수 #합성함수 #극한 #미분법 #평균변화율

#로그함수 #절대값 #로그미분법 #이계도함수

두 함수를 몫으로 표현된 함수, 합성함수, 음함수, 역함수, 매개변수로 표현된 함수 등

다양한 형태의 함수의 미분법에 대하여 알아 보자.

​

1. 몫의 미분법

가. 몫의 미분법​

위 함수는 도함수의 정의를 이용하여 다음과 같이 풀이할 수 있다.​

위와 같이 매번 도함수의 정의를 이용하여 도함수를 구하는 것은 복잡하고 시간이 많이

걸리게 되는데 몫의 미분법은 결과를 공식화하여 기억하자.​

[예제] 몫의 미분법을 이용하여​

【 몫의 미분법 】

두 함수 f(x), g(x) (g(x) ≠ 0)가 미분가능할 때

이와 같이 몫의 미분은 결과 공식을 외워 두자.​

n이 자연수일 때 다항함수 y = xn 의 도함수가 y' =n xn-1 이다. 그런데 몫의 미분법을 이

용하면 n이 정수일 때도 위 사실이 성립함을 알 수가 있다.​

①,②,③에서 알 수 있듯이 n이 양수일 때 뿐만 아니라 0이거나 음의 정수일 때에도 함수

y = xn 의 도함수 y' = n xn-1 이 된다. 즉, 임의의 정수 n에 대하여 y = xn 의 도함수는

y' = n x n-1 이 된다.

​

【 y = xn 의 도함수 (단, n은 정수) 】​

2. 합성함수의 미분법

가. 합성함수의 미분법

함수 y = (2x -3)3 의 도함수를 구하려면 다음과 같이 식을 전개한 후 미분해야 한다.​

이 처럼 다항함수의 차수가 조금만 높아도 전개한 다음 미분하는 것은 여간 복잡한 것이 아니다.

따라서 함수를 전개하지 않고 미분할 수 있는 방법이 있다면 그 방법을 이용하는 것이 빠르고 계산과정도 간단하다.

합성함수의 도함수가 어떻게 나타나는지를 확인해 보면 그 방법을 구체적으로 확인할 수 있다.

두 함수 y = f(u), u = g(x) 가 미분 가능할 때, 도함수의 정의를 이용하여 합성함수

y =f (g(x))의 도함수를 구해 보자.​​

위 식에서 앞, 뒤 두 극한 값을 찾으면 함성합수의 도함수를 구할 수 있다.

① 앞 함수의 극한 값

g(x+h) = B, g(x) = A 라고 하면 함수 y = g(x)미분 가능하므로 연속이다.

따라서 h → 0 일 때, g(x+h) → g(x) 이므로 h → 0 이면 B → A 이다.​

② 뒤 함수의 극한값은 도함수의 정의에 의해 g'(x)가 된다.

따라서 ①, ② 에 의해 합성함수 y = f(g(x))의 도함수는 다음과 같다.​

[예제] 함성합수의 미분법을 이용하여 함수 y = (2x-3)3의 도함수를 구해 보자.

이 함수를 f(u)=u3 과 g(x) = 2x-3의 합성합수라고 하면​

[합성함수의 미분법]​

【 합성함수의 미분은 (겉미분) × (속미분)】

합성함수 y = f(g(x))의 도함수를 다음과 같이 기억하자.

① 바깥 쪽 함수 f(x)를 미분하고 안의 함수 g(x)는 그냥 둔 다음 ☜ 겉미분 f'(g(x))

② 안쪽 함수 g(x)를 미분하여 ☜ 속미분 g'(x)

③ 겉미분과 속미분을 곱한다. ☜ f'(g(x)) · g'(x)

위 사실을 적용해 보면​

3. 매개변수로 표현된 함수의 미분법

x = t - 1, y = t2 + 1 과 같이 변수 t에 대한 함수 x, y가 주어져 있을 때, 함수 x, y를 각각

t에 대한 한수로 볼 수 있지만 중복되는 변수 t를 소거하여 y를 x에 대한 하나의 함수로 볼

수도 있다. 즉, x = t-1 에서 t = x+1 이므로 이를 y = t2 + 1에 대입하여 변수 t를 소거하면​

따라서 y는 t에 대한 함수이기도 하지만 x에 대한 함수이기도 하다.

이와 같이 두 변수 x, y의 함수 관계가 변수 t를 매개로 하여 x = f(t), y = g(t)의 꼴로 표현

될 때, 변수 t를 매개변수라 하고 x = f(t), y = g(t)를 매개변수로 표현된 함수라고 한다.

매개변수로 표현된 함수 x = f(t), y = g(t)의 도함수를 구하기 위해서는 매개변수 t를 소거

하여 y = f(x) 꼴의 함수로 고친 다음 미분해야 한다.​

함수 x = f(t), y = g(t)가 t에 대하여 미분가능하고 f(t) ≠ 0이면 x=f(t)의 역함수가 존재하고 t는 x의 함수이므로

y = g(t)도 x의 함수로 볼 수 있다.

따라서 t의 증분 △t에 대한 x의 증분을 △x. y의 증분을 △y라 하면 △x→0 일 때 △t→0 이고,​​

【 매개 변수로 표현된 함수의 미분법】

x = f(t), y = g(t) 가 t에 대하여 미분가능하고 f'(t) ≠ 0 이면​

예제 : 매개변수로 표현된 함수의 미분법​

4. 음함수의 미분법

가. 음함수의 미분법

일반적으로 함수는 정의역의 원소 x와 공역의 원소 y 사이의 관계식으로 표현할 수 있다.​

왼쪽과 같이 y = f(x)의 꼴일 때 y를 x의 양함수(Explicit function)라고 하고, 오른쪽과 같이 f(x,y) = 0 의 꼴일 때

y를 x의 음함수 (Implicit function)라고 한다.

음함수 f(x,y) = 0 을 양함수 y = f(x)의 꼴로 고칠 수 있다면 양함수로 변형한 다음 미분하여 도함수를 구할 수 있다.

하지만 음함수 x3+y2+2y+3 = 0 처럼 양함수로 고치기가 어려운 함수들에 대하여 음함수를 양함수 y = f(x)의 꼴로

고치지 않고 바로 미분할 수 있는데 이를 음함수의 미분법이라고 한다.

양함수든 음함수든 미분계수와 도함수는 모두 정의역의 원소인 x의 변화량에 따른 함수값 y의 변화량의 극한을 뜻하는

것이고 이것을 dy/dx라는 기호를 써서 나타낸다. 음함수는 비록 f(x,y) = 0 의 형태를 띠고 있다고는 하지만 y가 x에 대한

함수라고 가정을 한다.

따라서 문자 y를 포함하고 있는 항을 x에 대하여 미분할 때에는 y를 x의 함수로 보고 합성함수의 미분법을 적용하여

미분하는 것이 음함수의 미분법의 핵심이다.

음함수 x2 + y2 = 1 에 위의 사실을 적용해서 양변을 x에 대하여 미분하면​

[예제] 음함수의 미분법을 이용하여 x3+y2+2y+3=0 의 도함수를 구해 보자.

양변을 x에 대하여 미분하면​

【음함수의 미분법】

x의 함수 y가 음함수 f(x, y) = 0 의 꼴로 주어졌을 때, y를 x의 함수로 보고 각 항을 x에 대하여 미분하여 dy/dx를 구한다.

예제 : 음함수의 미분법을 이용하여 xy = 4 의 도함수 dy/dx를 구하여라.

[풀이] y를 x의 함수로 보고 각 항을 x에 대하여 미분하면 ​

나. y = xr 의 미분법 (단, r은 유리수)

몫의 미분법을 사용하여 n이 정수인 범위에서 (xn)' = nxn-1 이 성립한다는 것을 알았다.

이제 음함수의 미분법을 이용하면 n이 유리수인 범위에서도 성립한다는 것을 알 수 있다.

y = xr (r은 유리수)을 미분해 보자

임의의 유리수 r에 대하여 r = n/m (m,n은 정수, m≠0)으로 나타낼 수 있다.​

이 식의 양변을 x에 대하여 미분하면 음함수의 비분법에 의하여​

【 y = x^r 의 도함수 (단, r는 유리수】​

[예제]​​

5. 역함수의 미분법

미분가능한 함수 y = f(x)의 역함수 y = f-1 (x)가 존재하고 미분가능할 때 f-1(x)의 도함수를 구해보자.

역함수의 관계에 의해 f(a) = b 이면 f-1(b) = a 이므로 함수 y = f-1 (x)의 x = b 에서의 미분계수를 구한 다음,

이것이 y = f(x)의 x=a 에서의 미분계수와 어떤 관계가 있는지 살펴 보자.

도함수의 정의에 의해 함수 y = f-1(x) 의 x = b에서의 미분계수는​

아래 그림과 같이 f-1(b)=a이고 f-1(b+h)=a+h' 이라고 하면 h' → 0 이므로

이를 미분의 정의에 의해 미분을 하면​

이것을 정리하면 다음과 같이 표현할 수 있다.​

이제 좀 더 범위를 확장하여 앞에서 배운 음함수의 미분을 이용하여 함수와 그 역함수의

도함수 사이의 관계를 확인해 보자.

y = f-1 (x) 라 하면 x = f(y)이고 양변을 x에 대하여 미분하면 좌변과 우변은 각각​

한편, x = f(y) 에서 양변을 y에 대하여 미분하면 dx/dy = f'(y) 이므로 다음이 성립한다.​

따라서 역함수의 미분법을 이용하면 역함수를 직접 구하지 않고도 역함수의 도함수를 구할 수 있다.

【 역함수의 미분법 】​

[예제] 함수 f(x)=x2 (x≥0) 의 역함수를 y=f-1 (x)라 하자. 역함수의 미분법을 이용하여

(f-1)'(4)의 값을 구하여라.

<풀이> f-1 (4) = a 라 하면 f(a) = 4 이므로 a2=4 a=2 ∵ a ≥ 0

역함수의 미분법에 의해​

[참고]​

가. 우리가 다루는 대부분의 함수는 일차함수 y = ax+b, 이차함수 y=ax2+bx+c, 지수함수 y= ax, 로그함수 y= log ax,

      삼각함수 y = sin x 등의 함수가 모두 양함수로 표현되어 있어야 한다고 생각하기 쉽다. 예를 들어 함수의 표현에

      있어서 y5 =2x+1 보다는 y=(2x+1)1/5 이라는 형태에 익숙하고 편안함을 느낀다. 하지만 모든 함수가 항상 양함수

      로 표현이 가능한 것은 아니며, 양함수로 표현한다고 하더라도 복잡한 형태를 띠게 되는 경우가 많으므로

      dy/dx = 1/dx/dy는 이런 상황에서 큰 역할을 한다.

      예를 들어 음함수 y3+y2=3x+2를 y=f(x)로 바꾼 다음에 도함수 dy/dx= f'(x)를 구하는 것은 쉽지 않다.

      하지만 양변을 y에 대하여 미분을 하면​

나. 기호 dy/dx 는 독일의 수학자 라이프니츠가 처음 사용한 기호로서 dy를 dx로 나눈 분수가 아니라 그대로 하나의 도함수

      를 나타낸다. 하지만 합성함수나 역함수의 미분법에서는 dy/dx를 형식적으로 분수와 같이 다룰수 있는데,

      이는 라이프니츠 미분법의 장점이라고 할 수 있다.

      앞에서 배운 매개변수로 표현된 함수의 미분법에서도​

#몫의미분법 #몫 #도함수 #미분법 #합성함수 #겉미분 #속미분 #매개변수 #함수

#음함수 #양함수 #역함수 #라이프니츠 #로그함수 #삼각함수 #지수함수 #분수

#일차함수 #이차함수

미분의 개념을 이야기할 때 미분계수는 어떤 함수의 특정점에서 접선의 기울기값이라고 했다.

특정 점에서 접선의 기울기를 구하기 위하여 극한값을 구하는 과정도 알아 보았다.

그런데 함수 y = f(x)에 대하여 f'(1), f'(2), f'(3) … f'(100)을 구한다면 미분계수의 정의

를 이용하여 미분값을 구한다면 평균변화율의 극한값을 100번을 계산하여야 하는데 이는

번거롭고 효율적이지 못하다. 이런 경우에 x에서의 f'(x)를 함수값으로 하는 새로운 함수

y = f'(x)를 구하여 x값을 대입하면 보다 효율적으로 미분값을 계산할 수 있다.

이와 같이 어떤 함수 y = f(x) 함수에서 x값에 있어서의 미분값으로 하는 새로운 함수

y = f' (x)를 y = f(x)의 도함수라고 한다.

​

1. 도함수의 뜻

​

가. 도함수의 정의

함수 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는​

따라서 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는 a의 값을 2배하여 구할 수 있다. 즉,

f'(1) = 2, f'(√2) =2 √2, f'(π) = 2π, … f'(x) = 2x 이다.

일반적으로 함수 y = f(x)가 정의역 X에서 미분가능하면 정의역에 속하는 모든 x에 대하여

미분계수 f'(x)를 대응시키는 새로운 함수​

이를 그림으로 나타내면 다음과 같다.

이 때, 함수 f'(x)를 f(x)의 도함수라고 하고, 이것을 기호로

함수 y = f(x) 에서 그 도함수 f'(x)를 구하는 것을 함수 y = f(x)를 x에 대하여 미분한다고 하고 그 계산법을 미분법이라고

한다.​

【평균변화율, 미분계수, 도함수의 비교】

함수 y = f(x) 에서​

   ① 구간에서 x의 증분과 y의 증분의 비율

   ② 기하학적 의미 : 두 점 P(a, f(a), Q (b, f(b))를 지나는 직선의 기울기​

   ① 특정한 값 x = a 에서 평균변화율의 극한

   ② 기하학적 의미 : 곡선 y = f(x) 위의 점 P(a, f(a) 에서의 접선의 기울기​

   ① 특정값이 아닌 정의역에 속하는 임의의 x에 대한 미분계수 함수

   ② 기하학적 의미 : 곡선 y = f(x) 위의 임의의 점 (x, f(x))에서의 접선의 기울기

​

2. 미분법의 공식

도함수의 정의에서 도함수가 존재한다면 주어진 함수의 도함수를 구할 수 있게 된다.

그런데 도함수를 구할 때 정의에 의한 극한의 식으로 도함수를 구하기는 번거롭게 복잡

하다. 따라서 도함수를 구할 때 정의에 의해서 구하는 것보다 공식으로 도함수를 구하면

쉽고 편리하게 구할 수 있다.

​

가. 도함수의 정의에 이용하여 함수 f(x) = xn (n은 양의 정수)의 도함수를 구해 보자.​

인수분해 하면​

나. 상수함수 f(x) = C (C는 상수)의 도함수는

상수함수는 모든 점에서의 접선의 기울기가 항상 0이라는 것을 알 수 있다.

한편 아래의 미분법의 공식과 함수 y = xn 의 미분법을 이용하면 도함수의 정의를 이용하지

않더라도 다항함수​

의 도함수를 구할 수 있다.

【미분법의 도함수】

 두 함수 f(x), g(x)의 도함수가 존재할 때

   ① y = cf(x) 이면 y' = c f'(x) (단, c 는 상수)

   ② y = f(x) ± g(x) 이면 y' = f'(x) ± g'(x) (복부호 동순)

   ③ y = f(x) g(x) 이면 y' = f'(x) g(x) + f(x) g'(x) 가 된다.

또한 세함수 f(x), g(x), h(x)가 미분가능하면 함수 y = f(x) g(x) h(x) 도 미분가능하고

y' =f'(x) g(x) h(x)+ f(x) g'(x) h(x)+ f(x) g(x) h'(x) 이다.

​

다. 구간별로 정의된 함수의 도함수

구간별로 정의된 함수

f(x)= x (x < 0), x3 (x≥0) 의 도함수를 구할 때

각 구간의 도함수를 구하여 다음과 같이 나타내는 잘못을 해서는 안된다.

f'(x) = 1 (x <0), 3x2 (x ≥0)

구간의 경계가 되는 x = 0에서 평균변화율의 우극한은 0, 좌극한은 1로 같지 않기 때문에

x = 0 에서의 미분계수는 존재하지 않게 된다.

따라서 아래와 같이 나타내야 한다.

f'(x) = 1 (x <0), 3x2 (x >0)

일반적으로 구간별로 정의된 함수가 주어졌을 때, 그 구간의 경계점에서의 미분가능성은 알

수 없다. 경계점에서 미분가능하려면 미분계수가 존재해야 한다. 즉, 경계점에서의 평균변

화율의 극한이 존재해야 하므로 반드시 우극한과 좌극한이 서로 같은지 확인해야 한다.

참고로​

x = a 를 기준으로 나눠서 정의된 다항함수에서의 기하학적인 의미의 y = f(x)의 그래프가

x = a 에서 이어져 있고, 우극한에서의 접선의 기울기와 좌극한에서의 접선의 기울기가

같아야 한다.

​

#도함수 #비분 #우극한 #좌극한 #기하학 #다항함수 #기울기 #미분계수 #함수 #경계점

#평균변화율 #극한 #접선 #정의역 #방정식 #상수 #상수함수