1. △ (환상) 결선
▣ 환상 △ 결선은 3개의 상을 연속하여 상의 끝 부분을 다른 상의 첫 부분을 연결한 것
으로 우리말로는 환상결선이라고 한다.
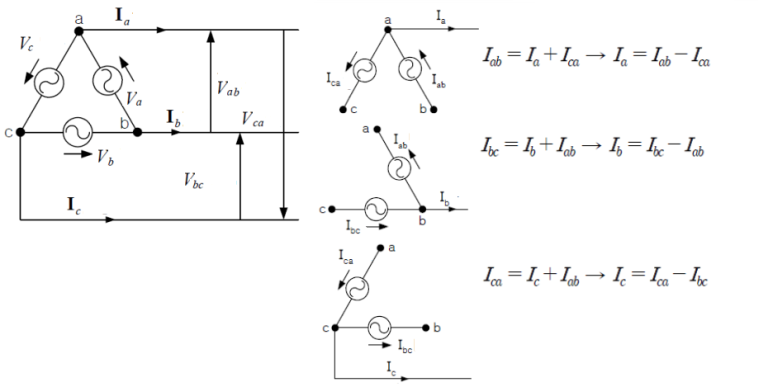
▣ 환상(△)결선에서 상전압, 선간전압, 상전류, 선전류의 관계는 다음과 같다.
⊙ 상전압 Vp = Va = Vb = Vc
⊙ 선간전압 VL = Vab = Vbc = Vca
⊙ 상전류 Ip = Iab = Ibc = Ica
⊙ 선전류 IL= Ia = Ib = Ic
⊙ 선간전압 VL = 상전압 Vp
⊙ 선전압 IL = √3 × 상전류 Ip ∠ -30 ˚
▣ 선전류는 상전류의 √3배이고 위상은 30˚ 뒤진다.
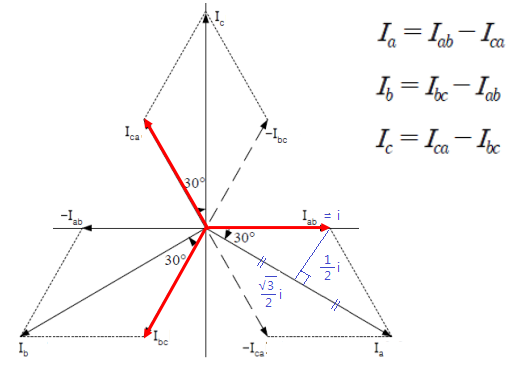
▣ 상전류와 선전류의 위상관계를 벡터 연산자 a를 이용하여 알아보자.
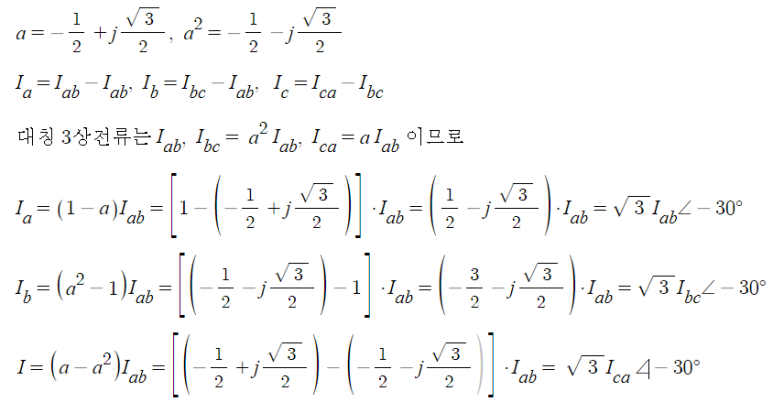
▣ △결선에서는 선간전압과 상전압이 크기와 위상이 같다.
⊙ VL = Vp ∠ 0˚
▣ 선전류는 상전류의 √3배이고 위상은 π/6 만큼 뒤진다.
⊙ IL = √3 Ip ∠ - π/6 (-30˚)
▣ n 상일 경우
⊙ 선간전압 VL = 상전압 Vp
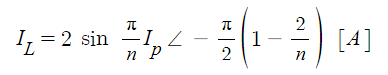
▣ 위 식에 3상과 6상을 적용해 봅시다.
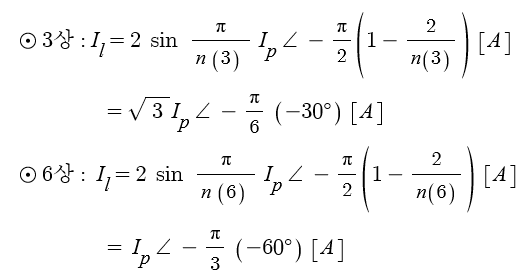
가. 소비전력 = 유효전력
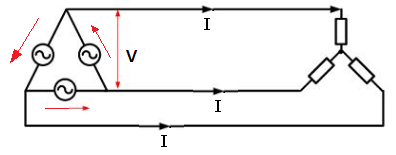
▣ △결선의 전원에서 전력을 공급하게 되면 한상에서 공급하는 전력 Pa = 기전력 (E) ×
전류 (I)가 된다. 이는 피상전력이고 부하에 공급되는 유효전력 P = 기전력 (E) × 전류 (I)
× cos θ 가 된다. 이 때 기전력 E = 선간전압 (V) / √3 이므로 부하에 공급하는 유효전력
P = 선간전압 (V) / √3 × 전류 (I) × cos θ 이 되고 3상에서 공급하는 유효전력은
P = 3 × (선간전압 (V) / √3 × 전류 (I) × cos θ) = √3 선간전압 (V) / × 전류 (I) × cos θ
이 된다.
▣ 3상 공급 전력
⊙ 피상전력 Pa = 3 Vp·Ip = √3 VL · IL
⊙ 소비(유효)전력 P = 3 Vp·Ip·cos θ = √3 VL · IL · cos θ
⊙ 무효전력 Pr = 3 Vp·Ip·sin θ = √3 VL · IL · sin θ
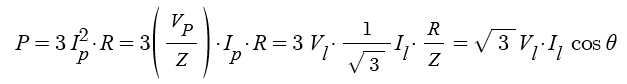
▣ n상 대칭 전력
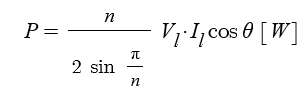
2. 부하의 Y- △ 변환
【 전제조건 】
▣ 전력공급( = 선간전압 × 선전류 )이 일정할 때, 즉 선전류와 선간전압이 일정하다고 할
때 부하 상의 임피던스, 전류 등의 변환을 말한다.
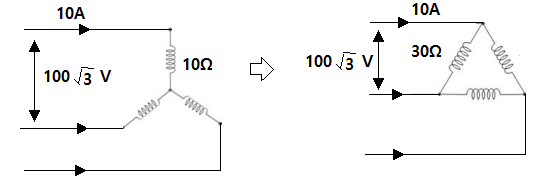
|
구분
|
선간
|
상
|
||||
|
전압 VL (V)
|
전류 IL (A)
|
전압 (V)
|
전류(A)
|
임피던스(Ω)
|
||
|
Y결선
|
100√3
|
10
|
100
|
10
|
10
|
|
|
△결선
|
100√3
|
10
|
100√3
|
10/√3
|
30
|
|
가. Y결선에서 △결선으로 변환
▣ Z△ = 3 ZY ※ 외우기 : Y3 ⇒ △ 영삼이는 산을 좋아했다.
나. △ 결선에서 Y 결선으로 변환
▣ ZY = 1/3 Z△
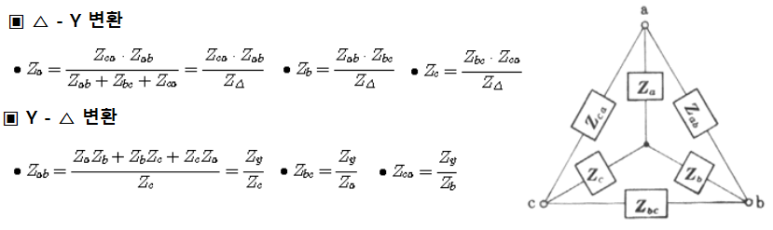
※ 외우는 법

예제 : 그림과 같은 △결선에서 전원전압이 200[V], Z = 3+j4 [Ω] 일 때 선전류를 구하라.
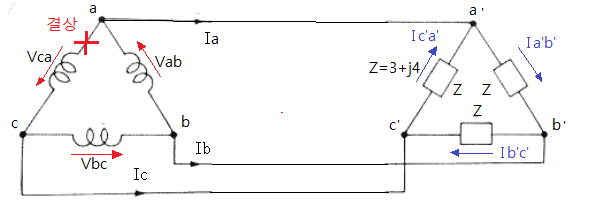
※ 전원전원이라 함은 선간전압을 말한다.
[참고] 전선로의 선간전압 = 공칭전압
기기, 기계의 선간전압 = 단자전압, 정격전압
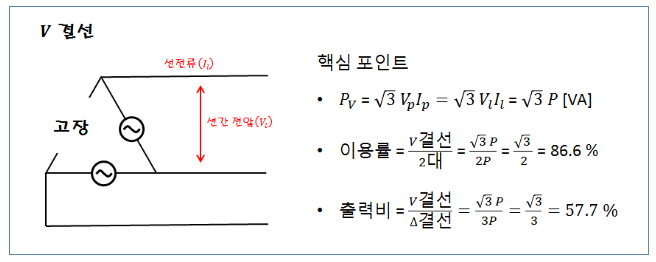
3. V결선
▣ V결선은 △결선 방식으로 전력을 공급하던 중 △결선의 한 상에 결상이 생긴 경우 2상
으로 3상 전력을 공급하는 형태이다.
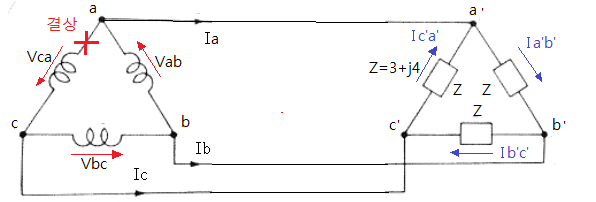
▣ Vca 상이 결상 되어도 Vca는 다음과 같은 전압이 발생하여 3상 전력 공급이 가능하다.
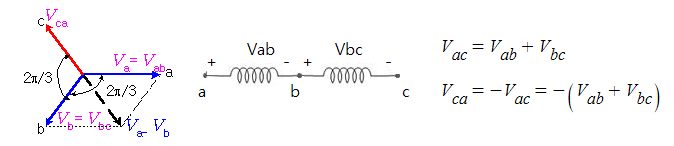
⊙ V결선에서는 한상이 결상이 되더라도 3상 전압이 발생한다. 하지만 전류의 경우에는
△결선에서는 선전류가 상전류의 √3배 이나 V결선에서는 상전류 = 선전류가 되어
공급되는 전력이 △결선 보다 1/√3배가 된다. 이를 벡터도를 보면서 알아 보자.

위 그림과 같이 전원의 상전류와 선전류는 같으나 △결선 부하의 상전류는 선전류의
1/√3배가 되므로 결국 3상의 공급전력은 P = √3 Vp·Ip가 되어 공급전력이 △결선에서
보다 1/√3배가 된다.
[종합하여 보면]
4. 2전력계법
▣ 2전력계법은 2개의 전력 측정을 이용하여 부하에 공급되는 3상의 피상전력(Pa),
유효(소비)전력(P), 무효전력(Pr)을 측정하는 방법을 말한다.
▣ 2전력계법의 측정방법은 아래 그림과 같다.
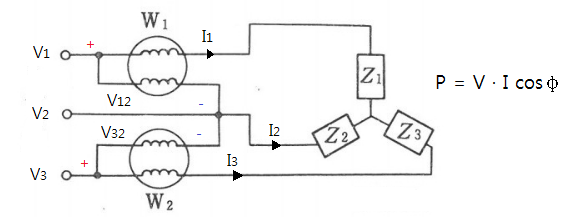
【전제조건】 전력계 1(W1)의 극성은 V1 : +, V2 : - 이며, 전력계 2(W2)의 극성은
V3 : +, V2 : - 이다. 따라서 전압 V12 = V1 - V2 이고 전압 V32 = V3 - V2이다.
▣ 전력계 W1과 W2의 전압 전류의 벡터도는 다음과 같다.
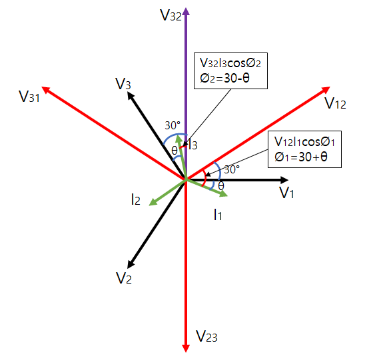
▣ 위 그림에서 전력계1에서 측정되는 전력 W1 = VI cos φ 이며 여기서 V=V12, I=I1
이며 V12 와 I1과의 위상차는 30˚+θ (V1과 I1과의 위상차)이다.
전력계2에서 측정되는 전력 W2 = VI cos φ 이며 여기서 V=V32, I=I3 이며
V32 와 I3 와의 위상차는 30˚-θ (V3과 I3과의 위상차)이다.
※ 3상 평형 전력이므로 V1과 I1과의 위상차와 V3과 I3과의 위상차는 같다.
【 종합 】 위 내용을 종합하여 보면 다음과 같다.
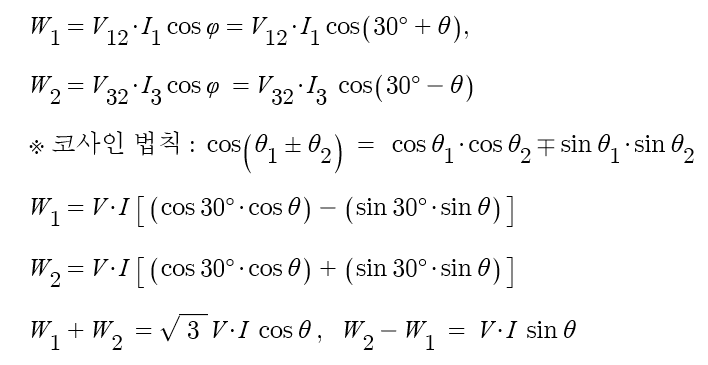
∴ 2전력계를 이용하여 측정할 수 있는 전력측 방법은 다음과 같다.
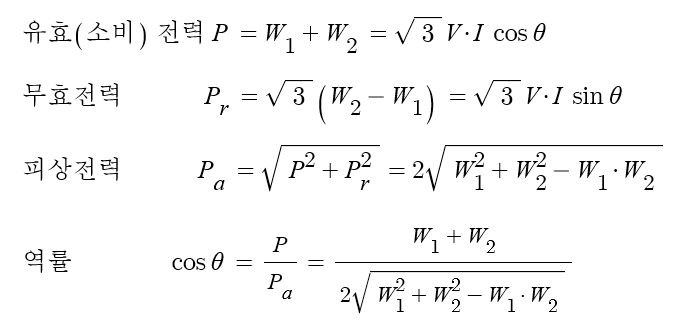
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 대칭좌표법 - 벡터 연산자 "a" (0) | 2022.01.09 |
|---|---|
| 대칭 n상 교류 회로 기출문제 풀이 (0) | 2022.01.08 |
| 대칭 n상 교류 이론 (0) | 2022.01.04 |
| 테브난의 정리, 노튼의 정리, 밀만의 정리, 기출문제 풀이 (3) | 2022.01.03 |
| 테브난의 정리, 노튼의 정리, 밀만의 정리, 기출문제 풀이 (2) | 2022.01.03 |
