재료역학(材料力學, Mechanics of materials)은 고체역학(Solid mechanics)이라고도 불리는 개념으로, 고체 재료의 강도와 역학적 움직임을 다룬다. 건축물, 교량, 기계부품, 압축용기 등 뼈대를 형성하고 힘을 지탱하는 구조물은 모두 재료역학의 대상이 된다.
재료역학의 주 목적은 구조물의 안전한 설계에 필요한 움직임 해석을 위해, 구조물 및 관련 물체에 작용하는 하중에 따른 응력, 변형, 변형률을 파악한다. 공학의 모든 분야에 있어 중요한 기초학문인 재료역학을 알아 보자.
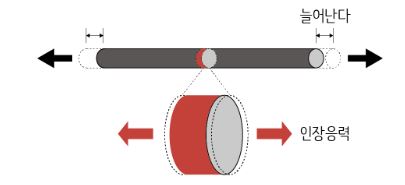
우선 외부에서 주어지는 힘 즉, 외력(外力)이 작용하면 재료 내부에는 이에 저항하는 힘이 생기는데 이를 응력(stress)이라 한다. 응력이란 단위 면적당 작용하는 힘을 말하며, 같은 힘을 주더라도 힘을 받는 면적이 넓으면 응력은 작아지게 된다.
응력을 식으로 나타내면 다음과 같다.

또한, 응력은 면에 수직으로 작용하는 성분과 면에 나란하게 작용하는 성분으로 나눠진다.
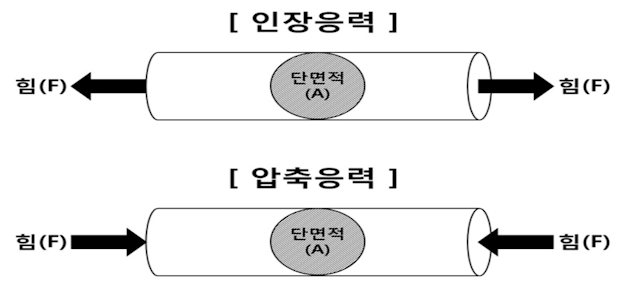
먼저 수직으로 작용하는 성분은 다시 2가지로 나뉘는데, 물체를 누를 때 생기는 응력을 '압축응력'이라고 하며 '압력'과 같은 의미이다. 반대로 잡아당길 때 생기는 응력을 '인장응력'이라고 한다. 예를 들어, 달콤한 엿을 망치로 내려치면 압축응력이 생기고, 반대로 엿을 양 손으로 잡아당기면 인장응력이 생긴다.

전단응력을 식으로 나타내면 다음과 같다.

수직 성분과 달리 물체의 면에 나란히 작용하는 응력으로는 '전단응력(shear stress)'이 있다. 물체의 단면을 절단하는 힘이 작용해 면에 나란한 방향으로 작용하는 응력을 전단응력이라 한다. 예를 들어 두꺼운 책을 놓고 책 표지에 손바닥을 댄 다음 옆으로 밀었을 때 책의 옆면이 틀어지면서 직사각형에서 평행사변형 모양으로 바뀌는 것이 바로 전단응력과 전단응력에 의한 변형의 예이다.
인장 응력에 의한 변화
어떤 재료에 인장응력이 가해진다고 생각해 보자. 막대를 양쪽에서 잡아 당기면 용수철 처럼 힘에 비례해서 길이가 늘어난다. 여기서 늘어난 길이를 변형이라고 하며, 변형을 원래 길이로 나눈 상대적인 값을 변형률(strain)이라 한다. 예를 들어, 10cm였던 고무줄을 잡아 당겨서 15cm가 됐다면 늘어난 5cm만큼을 원래의 길이인 10cm로 나누는 계산법이며, 이 인장응력에 따른 변형률은 5/10=0.5가 된다.
응력과 관련한 유명한 법칙 중 하나인 ‘후크의 법칙(Hook’s law)’에 따르면 탄성범위 내에서 ‘응력(σ)과 변형률(ε)은 비례한다’고 한다. 즉 σ = Е ε라는 수식으로 나타낼 수 있다.이 수식 중에 E는 비례상수로, 물질의 ‘탄성계수’라 하고 탄성계수가 큰 재료는 잘 늘어나지 않는 딱딱한 특성이 있다.
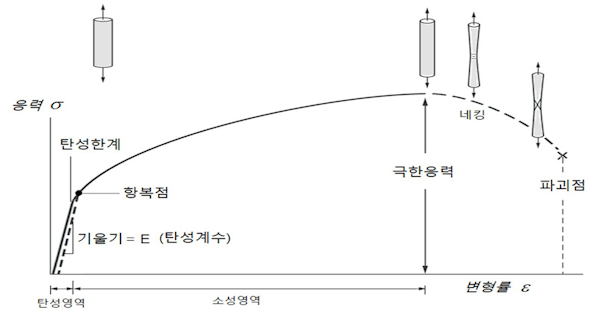
만약 재료를 세게 잡아당겨 응력이 탄성범위를 넘어서면, 재료는 원래의 상태로 돌아오지 못하게 된다. 고무줄을 적당히 잡아당겼다 놓으면 원래 모습으로 돌아가지만, 너무 세게 잡아 당기면 끊어져 버리듯이, 고체가 외부에서 탄성 한계 이상의 힘을 받아 형태가 바뀐 뒤, 가해지던 힘이 없어져도 더 이상 본래의 모양으로 돌아가지 않는 성질을 소성(塑性, plasticity)이라고 한다.
응력이 항복점(降伏點, 탄성과 소성의 경계점)까지 넘어서면 재료는 엿가락처럼 늘어나게 되는데 이것을 ‘소성변화’라고 한다. 여기서 더욱 세게 잡아 당기면 재료는 늘어지며 목이 가늘어지는 네킹(necking) 현상이 발생하고 결국은 끊어지게 된다. 따라서 구조물을 설계할 때 재료에 주어지는 응력이 항복점을 넘지 않도록 유의해야 한다.
반복 응력에 의한 피로와 파괴

항복점을 넘지 않더라도 응력이 반복해서 작용하면, 재료가 피로(fatigue)해져 파괴될 수도 있다. 철사를 이쪽저쪽으로 반복해서 구부리다 보면 결국 끊어지게 된다. 또 멀쩡하던 교량이 어느 날 특별한 이유 없이 무너지기도 한다. 이것은 반복 응력에 의한 재료의 피로 때문에 일어나는 현상이다.
저항성이 높은 '2차 단면 모멘트'
보통 구조물을 만들 때는 막대 형태의 재료(부재)가 가장 많이 쓰인다. 이 때 길이 방향으로 압축 힘을 받는 막대를 ‘기둥’이라 하며, 옆으로 놓여 수직 힘을 받는 막대를 ‘보’라고 한다. 또 비틀림을 받는 원통형 막대를 ‘축’이라 한다.
부재료들의 역할은 다르지만 누르거나 당기거나 비트는 등 응력이 작용하는 방향이 다르더라도 한계를 넘으면 파괴된다는 점은 모두 같다. 아래 그림처럼 나무판 의자로 쓰인 수평 보는 앉은 사람의 몸무게를 받아 휘어지는데, 가장 큰 전단응력을 받는 가운데가 먼저 부러지기 쉽다. 보의 윗 부분은 압축응력을 받고, 아랫 부분은 인장응력을 받아 휘게 되는데 화살표와 같이 이렇게 일종의 회전방향의 성격을 가진 외력을 모멘트(moment)라고 한다. 예를들어, 양손으로 연필을 부러뜨리듯이 힘을 줄 때 그러한 힘을 모멘트라고 한다.

모멘트가 가해지더라도 이를 버틸 강도를 생각하면 두껍고 튼튼하게 만들어야겠지만, 가능하면 재료를 덜 쓰고 가볍게 만드는 것이 좋다. 이를 경량화 설계라고 하며, 보의 단면 모양을 적절히 설계함으로써 최소한의 재료로 튼튼한 보를 만들 수 있다.

우리는 주변 건물 공사장에서 ㄷ자나 H자형 철강 구조물을 흔히 볼 수 있는데 이러한 철강 구조물은 꽉 찬 사각 막대 보다 가벼우면서 강도도 높일 수 있다. 이유는 단면 2차모멘트(moment of inertia)가 크기 때문인데, 단면 2차 모멘트는 다른 말로 단면 관성 모멘트라고 하며 휨 또는 처짐에 대한 저항을 나타내는 단면의 성질을 말한다. 모멘트가 가해지는 보에서 응력은 재료의 중심선(그림의 x-x)에서 멀어질수록 커진다. 따라서 그림에서 예를 든 H형강은 응력이 많이 발생하는 양 끝단에 질량을 집중함으로서 응력을 견디는 강성을 높일 수 있는 형태를 갖추게 된다.
안정적인 삼각형 형태, 트러스 구조

트러스 구조는 교량이나 건축물 등 우리 주변에서 흔히 찾아볼 수 있다. 대표적인 트러스 구조물로 에펠탑이다. 에펠탑의 총책임자는 구스타브 에펠이었지만, 실제 구조설계는 당시 수석 엔지니어였던 모리스 쾨클랭이다.

쾨클랭은 당시 철탑에 대한 비판과 안정성 논란을 불식시키기 위해 오랜 고민을 했다. 고심 끝에 철골 부재를 연결하여 작은 삼각형을 만들고, 이것을 다시 연결하여 큰 삼각형을 만드는 대대적인 트러스 격자 구조를 고안했습니다. 이러한 트러스 격자 구조로 만들어진 에펠탑은 구조설계 측면에서 최고의 걸작품으로 인정받고 있다.

우리는 재료역학 덕분에 현대문명의 뼈대를 이루는 구조물에 대한 체계적인 설계가 가능해졌다. 아무리 복잡한 형상과 구조를 갖는 구조물일지라도 컴퓨터의 도움을 받아 응력과 변형에 대한 구조해석을 할 수 있다. 인공 구조물 뿐만 아니라 세상에 존재하는 형체가 있는 모든 물체는 구조를 가지고 있다. 특히 잎사귀 줄기, 나뭇 가지, 동물 뼈 등 생명체 구조물은 자신만의 독특한 모양과 구조를 유지하고 있는데, 신비스러운 것은 외부에서 주어지는 힘과 중력의 무게를 잘 견딜 수 있도록 최적의 경량화 설계가 되어 있다는 사실이다.
#중량 #구조 #설계 #응력 #전단응력 #압력 #압축응력 #뼈대 #기둥 #보 #축
'소방설비기사 기계실기 이론' 카테고리의 다른 글
| 배관의 사용압력 및 허용 응력 (4) | 2024.06.02 |
|---|---|
| 스케줄 (SCH) 번호란 무엇일까 ? (0) | 2024.06.01 |
| 일반기체상수 (R)와 특정기체상수 (R')의 관계 (2) | 2024.05.26 |
| 기체의 밀도와 몰 질량 (몰분자량, 분자량) (2) | 2024.05.25 |
| 몰 (mol) 질량, 몰 부피, 입자수 사이의 관계 (2) | 2024.05.25 |