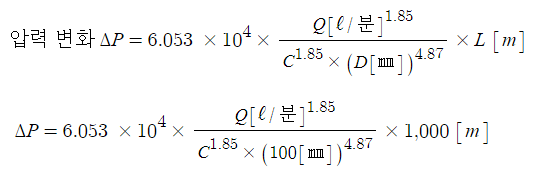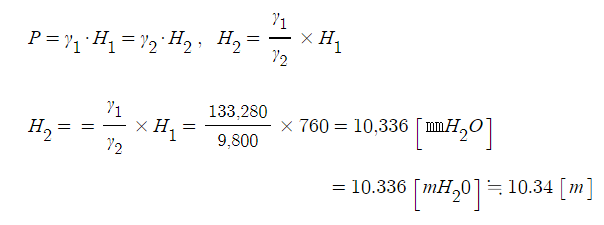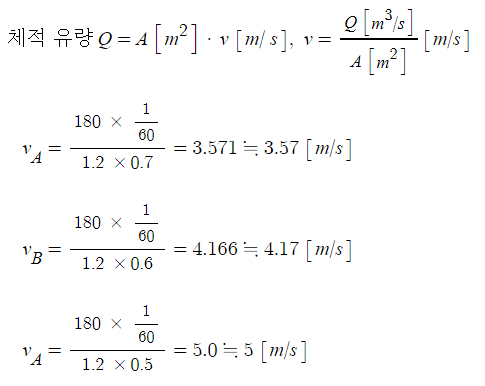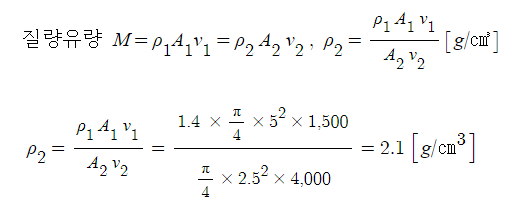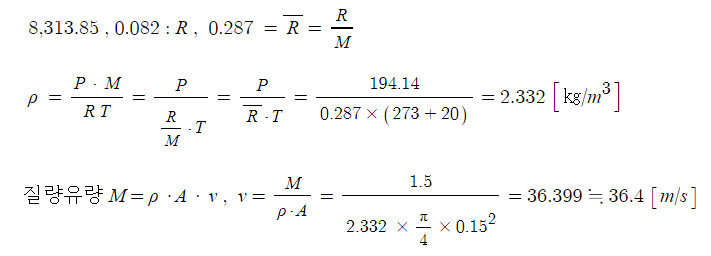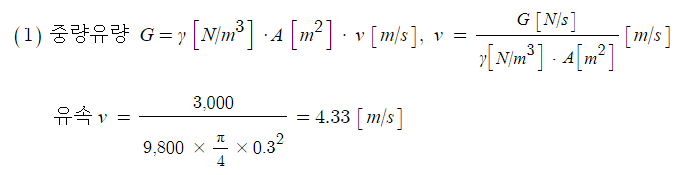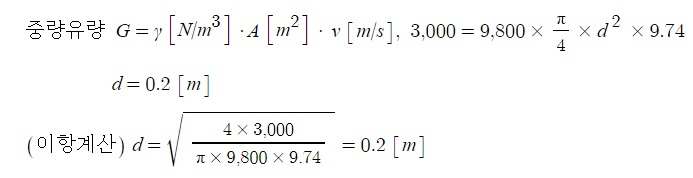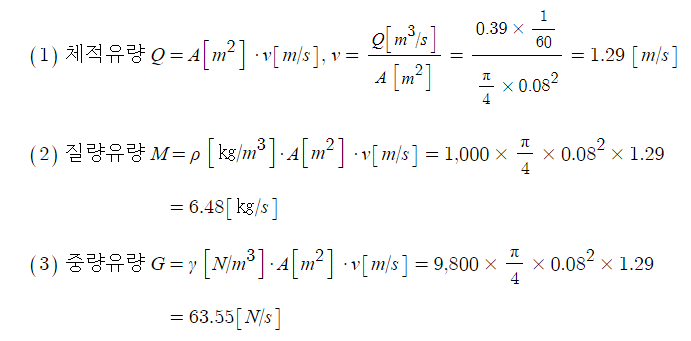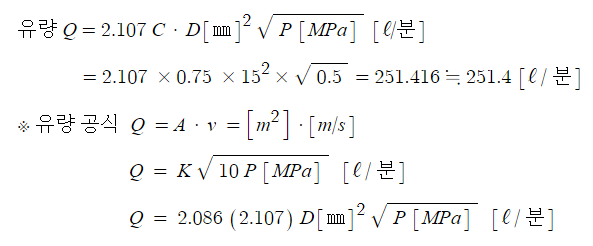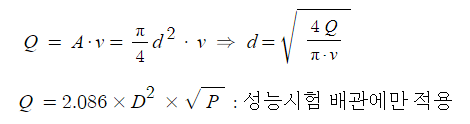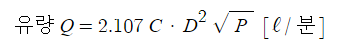아낌없이 주는 나무

【 참고 】 공식 정리

​

가. 플랜지 볼트에 작용하는 힘​

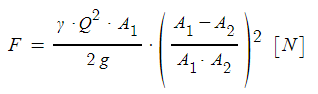
여기서, F : 플랜지에 작용하는 힘 [N]

             γ : 물의 비중량 (9,800 [N/㎥]

             Q : 유량 [㎥/s]

              A1 : 소방호스의 단면적 [㎡] = π/4·d2 [㎡]

              A2 : 노즐의 단면적 [㎡] = π/4·d2 [㎡]

               g : 중력 가속도 (9.8 [m/s2])

▣ 단면적 부분 계산식)​

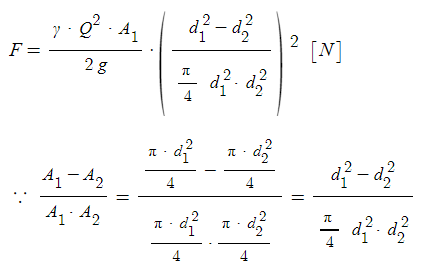
▣ 또 다른 계산식​

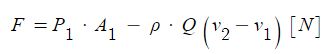
여기서, F : 플랜지에 작용하는 힘 [N]

             P : 압력 [Pa = N/㎡]

              A1 : 소방호스의 단면적 [㎡] = π/4·d2 [㎡]

              Q : 유량 [㎥/s]

              v1 : 소방호스의 유속 [m/s]

              v2 : 노즐의 유속 [m/s]

나. 노즐에 걸리는 반발력 (운동량에 따른 반발력)​

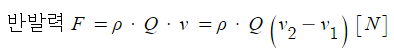
여기서, F : 노즐에 걸리는 반발력 (운동량에 따른 반발력) [N]

             ρ : 물의 밀도 (1,000 [N·s2/m4])

             Q : 유량 [㎥/s]

              v : 유속 [m/s]

              v1 : 소방호스의 유속 [m/s]

              v2 : 노즐의 유속 [m/s]

다. 노즐을 수평으로 유지하기 위한 힘​

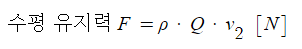
여기서, F : 노즐을 수평으로 유지하기 위한 힘 [N]

              ρ : 물의 밀도 (1,000 [N·s2/m4])

              Q : 유량 [㎥/s]

              v2 : 노즐의 유속 [m/s]

라. 노즐에 작용하는 반동력​

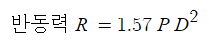
여기서, R : 노즐에 작용하는 반동력 [N]

             P : 방수압력 [MPa]

             D : 노즐 구경 [㎜]

​

【노즐에 걸리는 반발력】 (운동량에 따른 반발력)

가. 노즐에 걸리는 반발력 (운동량에 따른 반발력)​

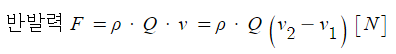
여기서, F : 노즐에 걸리는 반발력 (운동량에 따른 반발력) [N]

             ρ : 물의 밀도 (1,000 [N·s2/m4])

             Q : 유량 [㎥/s]

              v : 유속 [m/s]

              v1 : 소방호스의 유속 [m/s]

               v2 : 노즐의 유속 [m/s]

나. 유량​

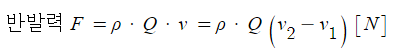
여기서, Q : 유량 (방수량) [㎥/s]

             A : 단면적 [㎡] = π/4·d2 [㎡]

             v : 유속 [m/s]

             d : 관의 내경 [m]

다. 유량​

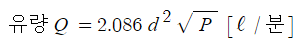
여기서, Q : 유량 [ℓ/min]

             d : 관의 내경 [㎜]

             P : 압력 [MPa = MN/㎡]

​

1. 옥외 소화전 1개를 개방하여 피토게이지로 방수압을 측정한 결과 0.6 [MPa]이었다.

    호스구경이 65 [㎜]이고 노즐구경이 20 [㎜]일 경우 노즐에 걸리는 반발력 [N]을 구하시오. [5점] ★★★★★

※ 노즐에 걸리는 반발력 (운동량에 따른 반발력]

      F = ρ · Q (v1 -v2) [N]

위 식을 적용할 때 유량은 지문에서 피토게이지로 측정한 압력이 주어졌으므로 다음 식을 이용하여 유량을 구한다.​

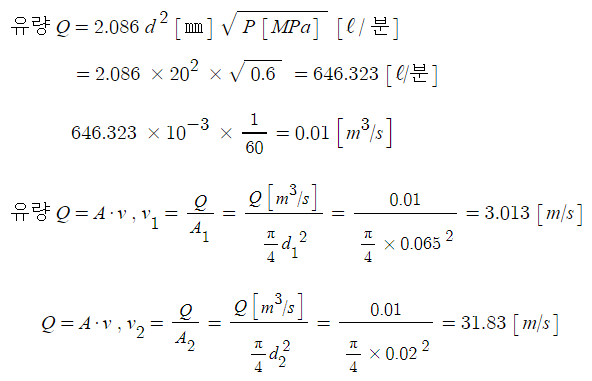
유량, 유속을 산정식에 대입하여 문제를 풀면

작용하는 힘 F =  ρ · Q (v1 -v2) [N]

                       = 1,000 [kg/㎥] × 0.01 [㎥/s] × (31.83-3.013) [m/s] = 288.17 [N]

※ 구경 (d) 값이 주어지지 않은 경우

   ⊙ 옥내 소화전 : d = 13 [㎜]

   ⊙ 옥외 소화전 : d = 19 [㎜]

​

2. 내경이 65 [㎜] 인 소방호스에 내경이 36[㎜]인 노즐이 부착되어 있다. 대기 중에 0.02 [㎥/s]의 방수량으로 방사할 경우

    노즐에 걸리는 반발력 [N]을 구하시오. [5점]  ★★★★★

노즐 반발력 F = ρ · Q (v1 -v2) [N]

                       = 1,000 [㎏/㎥] × 0.02 [㎥/s] × (19.648 - 6.027)[m/s] = 272.42 [N]

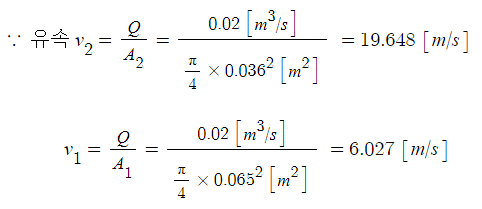
【노즐에 걸리는 반발력】 (운동량에 따른 반발력)

가. 노즐에 걸리는 반발력 (운동량에 따른 반발력)​

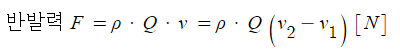
여기서, F : 노즐에 걸리는 반발력 (운동량에 따른 반발력) [N]

             ρ : 물의 밀도 (1,000 [N·s2/m4])

             Q : 유량 [㎥/s]

              v : 유속 [m/s]

              v1 : 소방호스의 유속 [m/s]

              v2 : 노즐의 유속 [m/s]

나. 유량​

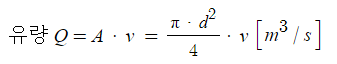
여기서, Q : 유량 (방수량) [㎥/s]

             A : 단면적 [㎡] = π/4·d2 [㎡]

              v : 유속 [m/s]

              d : 관의 내경 [m]

​

3. 지름이 10 [㎝]인 소방용 호스에 노즐구경이 3 [㎝]인 노즐 팁이 부착되어 있다.  3 [㎥/min]의 방수량으로 대기 중에 방사

    할 경우 다음 각 물음에 답하시오. (단, 유동에는 마찰이 없는 것으로 본다) [6점] ★★★★★

 가. 소방용 호스의 평균 유속 [m/s]을 구하시오.

 나. 소방용 호스에 부착된 노즐의 평균 유속 [m/s]을 구하시오.

 다. 소방용 호스에 부착된 플랜지 볼트에 작용하는 힘[N]을 구하시오.

[풀이]

가. 소방용 호스의 평균 유속 [m/s]을 구하시오.​

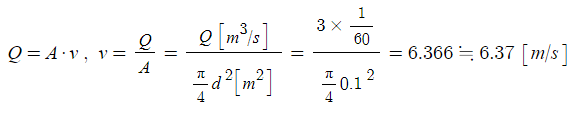
나. 소방용 호스에 부착된 노즐의 평균 유속 [m/s]을 구하시오.​

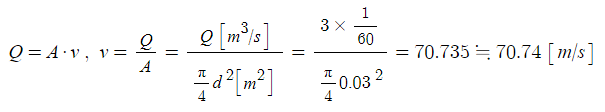
다. 소방용 호스에 부착된 플랜지 볼트에 작용하는 힘[N]을 구하시오.​

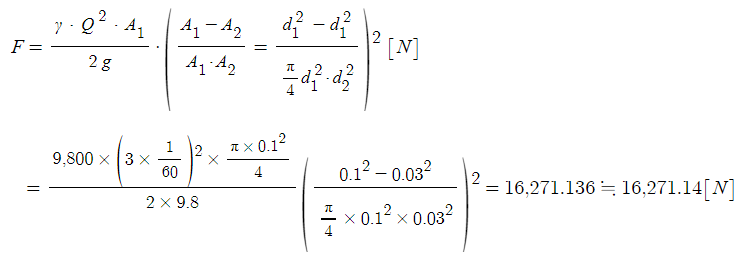
※ 앞쪽 계산 먼저하고 난 후 Ans × 뒷 쪽 분수 계산을 한다.

[해설] 플랜지 볼트에 작용하는 힘

① 플랜지 볼트에 작용하는 힘​

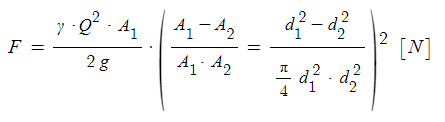
여기서, F : 플랜지에 작용하는 힘 [N]

             γ : 물의 비중량 (9,800 [N/㎥]

              Q : 유량 [㎥/s]

             A1 : 소방호스의 단면적 [㎡] = π/4·d2 [㎡]

             A2 : 노즐의 단면적 [㎡] = π/4·d2 [㎡]

              g : 중력 가속도 (9.8 [m/s2])

② 유량 · 유속​

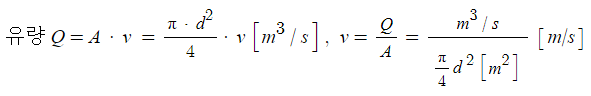
여기서, Q : 유량 (방수량) [㎥/s]

             A : 단면적 [㎡] = π/4·d2 [㎡]

             v : 유속 [m/s]

             d : 관의 내경 [m]

​

4. 옥내소화전설비의 노즐선단 방수압력이 0.3 [MPa]일 때 작용하는 반동력 [N]을 구하시오. [4점] ★★★​

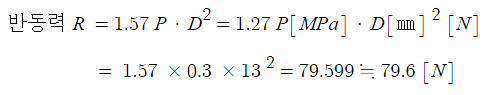
※ 노즐 구경이 주어지지 않은 경우

   ⊙ 옥내소화전 노즐구경 : 13 [㎜]

   ⊙ 옥외소화전 노즐구경 : 19 [㎜]

[해설] 노즐에 작용하는 반동력

    반동력 F = 1.57 P · D2 [N]

여기서, R : 노즐에 작용하는 반동력 [N]

             P : 방수압력 [MPa]

             D : 노즐 구경 [㎜]

​

5. 소방시설의 가압 송수장치에서 주로 사용하는 펌프로 볼류트 펌프와 터빈 펌프가 있다.

     이들 펌프의 특징을 비교하여 다음 표의 빈칸에 유·무, 대·소, 고·저 등으로 작성하시오.  [6점] ★★★★★

[해설] 소방용 펌프

소방용 펌프는 원심펌프를 사용하며 원심펌프에는 볼류트 펌프와 터빈 펌프가 있다.

  원심펌프 - 볼류트 펌프 : 임펠러의 날개(안내깃)가 없으며 고유량, 저양정(압력)에 사용

                 - 터빈 펌프 : 임펠러의 날개(안내깃)가 있으며 저유량, 고양정(압력)에 사용

​

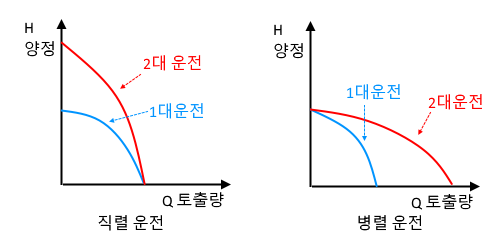
6. 펌프 2대를 병렬로 운전할 때와 펌프 1대를 운전할 때를 비교하여 그래프로 나타내시오.  [4점] ★★★★★

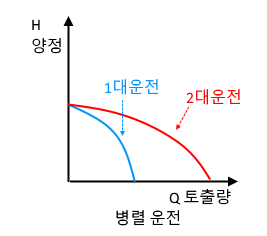
[해설] 펌프의 직렬 · 병렬 운전

7. 펌프에서 NPSH란 무엇인지 간단히 쓰고, 공동현상 (Cavitation)의 발생 한계 조건을 쓰시오. [5점] ★★★★

  가. NPSH : 물의 높이로 표시된 실제 흡입양정을 말하며, 펌프가 공동현상을 일으키지 않고 흡입가능한 압력을 물의

                     높이로 표시한 것

  나. 공동현상의 발생 한계 조건

    ① 공동현상의 발생한계 : NPSHav = NPSHre

    ② 공동현상이 발생하지 않음 : NPSHav > NPSHre

    ③ 펌프설계시 여유 : NPSHav ≥ NPSHre × 1.3

        ※ 여유율 30 % 를 둔다.

​

[해설] NPSH (흡입양정] (Net Positive Suction Head)

가. NPSH : 물의 높이로 표시된 실제 흡입 양정을 말하며 펌프가 공동현상을 일으키지 아니하고 흡입 가능한 압력을

                   물의 높이로 표시한 것

나. 펌프의 송수 조건

  (대기압 - 저항력의 합) ≥ 펌프에 의해 형성되는 진공 능력 (절대압)

  ※ 저항력 : 수면 (평상시 수면이 아닌 소요된 시간동안 물을 사용한 이후의 수면)으로 부터 펌프 임펠러 중심까지 흡입

                    과정에서의 저항력

     ① 흡입관 높이에 따른 낙차 압력

     ② 펌프 흡입측 마찰 손실 압력

     ③ 흡입관 내부에서의 포화증기압

​

다. NPSHav (유효흡입양정) = NPAHav =available

  ① 펌프의 설치조건에 따라 결정되는 펌프로 가해지는 흡입측으로 부터의 양정

  ② NPSHav (유효흡입양정)은 펌프 주변 배관의 설계에 따라 그 값이 달라진다.

​

라. NPSHre (필요흡입양정)

  ① 펌프기동에 필요한 흡입측 양정을 말하며 펌프회전에 의해 만들 수 있는 펌프 내부의 진공도에 의해 결정

  ② 펌프 제작시 결정되는 고유값 (설계시 변하지 않음)

  ③ NPSHre 가 클수록 펌프의 흡입능력은 저하

마. 공동현상의 발생 한계 조건

   ① 공동현상의 발생한계 : NPSHav = NPSHre

   ② 공동현상이 발생하지 않음 : NPSHav > NPSHre

   ③ 펌프설계시 여유 : NPSHav ≥ NPSHre × 1.3

​

8. 다음 조건을 참조하여 펌프의 유효흡입양정(NPSH)을 구하시오. [4점] ★★★★★

[조건]

  ⊙ 소화수조의 수증기압은 0.0022[MPa], 대기압은 0.1[MPa], 흡입배관의 마찰 손실 수두는 2 [m] 이다.

  ⊙ 흡상일 때 후드밸브에서 펌프까지의 수직거리가 3.8[m] 이다.

[풀이] NPSH = 10.496 - 3.8 - 2 - 0.224 = 4.172 ≒ 4.17 [m]

[해설]

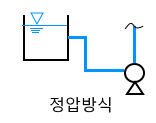
  ⊙ 정압방식 (압입) : NPSH = 대 + 거 - 마 - 수 [m]

                                                대 : 대기압, 거 : 수직거리, 마 : 마찰손실, 수 : 수증기압

  ⊙ 부압방식 (흡입) : NPSH = 대 - 거 - 마 - 수 [m]

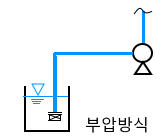
[해설] 흡입 NPSH (수면이 펌프 보다 낮을 경우)

    NPSH = Ha - Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

[참고] 압입 NPSH (수면이 펌프 보다 높은 경우)

     NPSH = Ha + Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

              Ha : 대기압 환산 수두 [m]

              Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

              Hf : 마찰 손실 압력 수두 [m]

              Hv : 포화증기압 환산수두 [m]

​

9. 다음은 어느 수계 소화설비에서 송수펌프의 계통을 나타내고 있다. 다음 그림과 조건을 참조하여 펌프의 유효흡입양정

     (NPSH)을 구하시오 [4점] ★★★★★

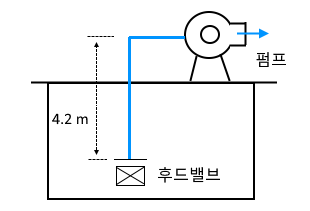
[조건]

   ⊙ 20 [℃]에서의 수증기압은 0.001[MPa]이다.

   ⊙ 펌프의 시동 최대 송수량은 2,400 [ℓ/min] 이다.

   ⊙ 펌프 흡입 배관에서의 마찰 손실은 0.002 [MPa](최대 송수시)이다. (단, 설계기준 온도는 20[℃]이며, 대기압은

         0.1[MPa], 물의 밀도는 1 [gf/㎤]로 하며 펌프 운전시 배관에서의 속도수두는 무시한다.)

[풀이]

   NPSH = Ha - Hh - Hf - Hv [m]

              = 10.196 - 4.2 - 0.203 - 0.101 = 5.692 ≒ 5.69 [m]​

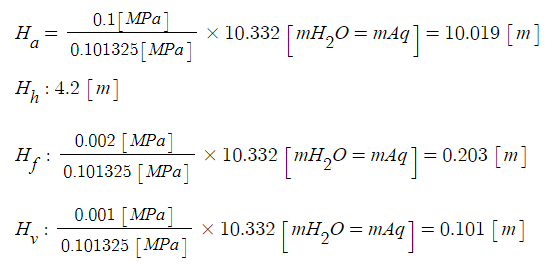
[해설] 흡입 NPSH (수면이 펌프보다 낮을 경우)

     NPSH = Ha - Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

※ 압력단위 환산

10. 다음 그림을 참조하여 해발 1,000[m] 에 설치된 펌프의 유효흡입양정 [NPSH]을 구하시오. [4점] ★★★★★

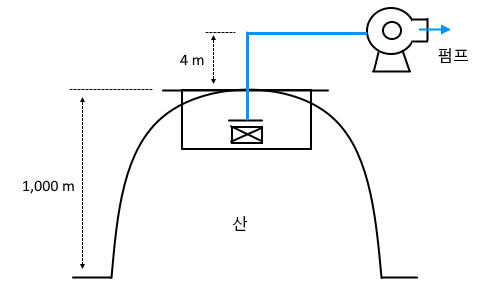
[조건] ⊙ 배관의 마찰손실수두는 0.5 [m] 이다.

          ⊙ 해발 0 [m]에서의 대기압은 0.0132[MPa]이다.

          ⊙ 해발 1,000 [m] 에서의 대기압은 0.0918[MPa]이다.

          ⊙ 물의 증기압은 0.0023 [MPa]이다.

[풀이] NPSH = Ha - Hh - Hf - Hv [m]

                     = 9.36 - 4 - 0.5 - 0.235 = 4.627 ≒ 4.63 [m]​

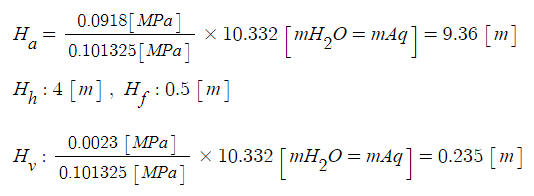
[해설] 흡입 NPSH (수면이 펌프보다 낮을 경우)

          NPSH = Ha - Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

※ 압력단위 환산

11. 다음 그림과 조건을 참조하여 펌프의 유효흡입양정 (NPSH)을 구하시오. [4점]  ★★★★★

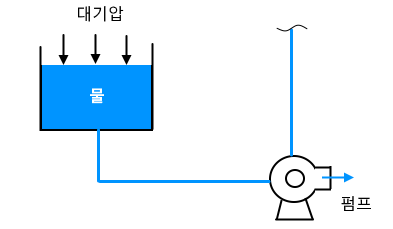
[조건]

  ⊙ 설계기준온도는 25 [℃] 이다.

  ⊙ 25[℃] 에서의 수증기압은 70 [㎜Hg]이다.

  ⊙ 펌프 흡입배관에서의 마찰손실수두는 0.3 [m] 이다.

[풀이]

▣ 유효흡입양정 NPSH = Ha - Hh - Hf - Hv [m]

                                      = 10.332 + 0.8 - 0.3 - 0.952 = 9.882 ≒ 9.88 [m]​

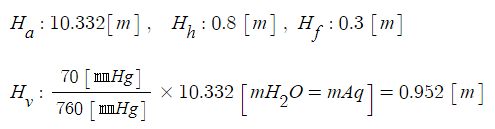
[해설] 압입 NPSH (수면이 펌프보다 높을 경우)

   NPSH = Ha + Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

※ 압력단위 환산

12. 펌프 흡입구에 설치된 연성계가 320[㎜Hg]일 때 이론 유효흡입수두는 몇 [m]인가? (단, 대기압은 760 [㎜Hg]이다) [4점]

        ★★★★★

[풀이] 부압방식일 때 펌프의 흡입측에 진공계 또는 연성계를 설치한다.

           진공계와 연성계의 압력은 수직거리수두, 마찰손실수두, 수증기압 수두를 모두 합한 값이 된다.

   NPSHav = Ha - (Hh + Hf + Hv) [m]

                  = 10.332 - 4.35 = 5.982 ≒ 5.92 [m]​

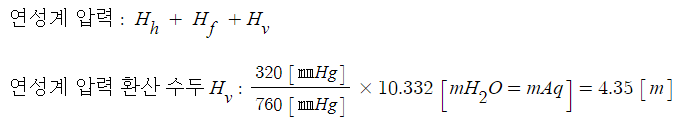
[해설] 흡입 NPSH (수면이 펌프보다 낮을 경우)

▣ 연성계는 부압방식(수면이 펌프보다 낮은 위치에 있는 경우)일 경우에 설치되므로 흡입 NPSH를 적용하며 연성계 압력

     에는 수직거리수두, 마찰손실수두, 포화증기압수두가 모두 포함된 값이다.

   NPSH = Ha - 연성계압력수두 (Hh + Hf + Hv ) [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m]

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

​

#플랜지 #볼트 #노즐 #반발력 #유량 #작용력 #밀도 #구경 #옥내소화전 #소화전

#운동량 #평균유속 #임펠러 #터빈 #원심펌프 #볼류트 #병렬운전 #직렬운전

#유효흡입양정 #NPSH #공동현상 #cavitation #포화증기압

1. 방사압력이 0.3[MPa]인 유체가 노즐을 통해 방사되고 있다. 유속 [m/s]을 구하시오.  [8점] ★★★★★​

[해설] 유속

▣ 토리첼리 정리​

여기서, v : 유속 [m/s]

            g : 중력 가속도 (9.8 [m/s2])

            H : 높이 [m]

             P : 압력 [kPa = kN/㎡]

             γ : 물의 비중량 (9.8 [kN/㎥]

⊙ 압력 P : 0.3[MPa] = 300[kPa] =300 [kN/㎡]​

2. 지상 30[m]의 창문으로 부터 구조대응 로프의 모래주머니를 자연낙하시켰을 때 지상에 도착할 때의 속도는 몇 [m/s]인

    가 ? [4점] ★★★

[풀이]​

[해설] 유속

▣ 토리첼리의 정리​

여기서, v : 유속 [m/s]

             g : 중력 가속도 (9.8 [m/s2])

             H : 높이 [m]

              P : 압력 [kPa = kN/㎡]

              γ : 물의 비중량 (9.8 [kN/㎥]

    ⊙ 높이 H : 30 [m]​

3. 길이 600[m]인 관로 속을 2.5[m/s]의 속도로 물이 흐르고 있다. 출구의 밸브를 1.3초 후에 잠그면 압력 상승 [kPa]은 얼마

     인가 ? (단, 수관속의 유속 a = 1,000 [m/s]이다)  [4점] ★★★

[풀이]​

여기서, △P : 상승압력 [kPa]

             α : 배관속의 유속 [m/s]

             v : 유속 [m/s]

            g : 중력가속도 (9.8 [m/s])

4. 내경이 25 [㎜]인 급수배관에 정상류가 180 [ℓ/min] 으로 흐를 때 속도수두 [m]는 얼마인가 ? (단, 중력가속도는 9.8[m/s]

    이다.) [3점] ★★★★★​

[해설]

가. 토리첼리의 정리​

여기서, v : 유속 [m/s]

            g : 중력가속도 (9.8 [m/s2])

            H : 높이 (속도수두)[m])

            γ : 물의 비중량 (9.8 [kN/㎥])

            P : 압력 [Pa = N/㎡]

나. 유량​

여기서, Q : 유량 [㎥/s]

              A : 배관의 단면적 [㎡] = π/4 · d2 [㎡]

              v : 유속 [m/s]

              d : 내경 [m]

5. 소화용수를 어떤 고층건물 옥상에서 쏟아 부었다. 소화용수가 떨어진 뒤 3초가 지날 때의 낙하속도는 얼마인가 ?

  ▣ 중력가속도 = 속도 / 시간, 속도 = 중력가속도 × 시간​

[해설] 낙하 속도

   중력가속도 = 속도 / 시간 , g = v / t, v = g · t [m/s]

   여기서, v : 낙하속도 [m/s]

                g : 중력가속도 (9.8 [m/s2])

                t : 시간 [s]

6. 다음 그림과 조건을 참조하여 개방된 고가수조에서 배관을 통하여 물을 방수할 때 ② 지점에서의 방출압력 [kPa]을 구하

    시오. [5점] ★★★

  ⊙ 대기는 표준대기압 상태이다.

  ⊙ 배관의 안지름은 100 [㎜] 이다.

  ⊙ 배관의 길이는 250 [m] 이다.

  ⊙ 방출유량은 2,500 [ℓ/min]이다.

  ⊙ 총 마찰손실수두는 7 [m] 이다.

  ⊙ 방출압력을 구할 때 계기압력으로 구한다.

[풀이] 베르누이의 연속방정식으로 풀어 보면​

위 식에서 수조의 표준대기압 = "0", 수조의 유속 = "0"을 대입하면​

[참고] 적정소방수류가 도달된 최대 높이​

여기서, V : 적정 소방수류가 도달한 최대 높이 [m]

             H : 건물로 부터 소화노즐까지의 거리 [m]

             Q : 유량 [ℓ/s]

  ⊙ H (건물로 부터 소화노즐까지의 거리) : 15 [m]

  ⊙ Q (유량) : 1,000 [ℓ/min] × 1/60​

7. 안지름이 155[㎜]인 관으로 1시간 30분 동안 60 [ton]의 물을 350 [m] 떨어진 곳으로 송수할 때 가하여야 할 필요한 압력

    [kPa]을 구하시오. (단, 마찰손실계수는 0.03이다.) [5점] ★★★★★

※ 달시-웨버의 식을 이용​

[ 압력 환산]

1[atm] = 760 [㎜Hg]

           = 0.101325 [MPa]

           = 101.325 [kPa]

           = 101,325 [Pa]

           = 10.332 [mAq = mH2O]

           = 10,332 [㎜Aq = ㎜H2O]

            = 1,013 [bar]

8. 수평으로 된 어느 소방배관의 레이놀즈수가 1,000으로 유체가 흐르고 있다. 유량이 200 [ℓ/min], 배관의 길이 100[m],

    관지름이 40 [㎜] 일 때 다음을 구하시오. [4점]  ★★★★★

 가. 배관의 마찰손실 수두 [m]를 구하시오. (단, 달시 - 웨버의 식을 이용하여 구할 것)

 나. 출발점의 압력이 0.8[MPa]이라면 끝지점의 압력 [MPa]을 구하시오. (단, 소수점 여섯째 자리까지 구하시오.)

[풀이]

 가. 배관의 마찰손실 수두 [m]를 구하시오. (단, 달시 - 웨버의 식을 이용하여 구할 것)

    ※ 달시-웨버의 식은 마찰손실계수, 관의 길이, 속도와 관경에 의한 손실수두를 구하는 식이다.

나. 출발점의 압력이 0.8[MPa]이라면 끝지점의 압력 [MPa]을 구하시오. (단, 소수점 여섯째 자리까지 구하시오.)

※ 관로 등의 입 · 출구의 한쪽의 에너지가 주어지고 다른 쪽의 에너지를 물어 보는 문제는 베르누이의 연속방정식으로

    풀이를 한다.​

⊙ 위 식에서 수평배관이므로 위치수두와 관경 및 유량(유속)이 입구와 출구가 같으므로 속도수두와 위치수두가 입 · 출구

     에서 같게 되어 다음과 같이 수식을 변경할 수 있다.​

9. 수평으로 곧게 설치되어 있는 40[m] 길이의 배관내에 유량 300 [ℓ/min]의 물이 흐르고 있다. 배관 말단의 수압 [MPa]을

    구하시오. (단, 배관인입측의 수압게는 0.4[MPa] 을 가리키고 있으며, 구경 40 [㎜] 강관의 1 [m]당 마찰손실에 의한 압력

    강하는  △P = 1.08 × 10-7 × Q1.85 이며 Q는 유량 [ℓ/min]이다.)

[풀이]

  △P = 1.08 × 10-7 × Q1.85 × 40 [m] = 0.165 [MPa]

  ∴ 배관 끝 부분의 압력 = 입구측 압력 - 마찰손실 압력  = 0.4[MPa]-0.165 [MPa] ≒ 0.24 [MPa]

[해설] 배관 끝 부분의 압력 = 배관 입구측 압력 - 마찰손실 압력

   ⊙ 배관 입구 부분의 압력 : 0.4 [MPa]

   ⊙ 마찰손실 압력 : 문제의 단서에서 1 [m] 당 마찰손실에 의한 압력강하는

     △P = 1.08 × 10-7 × Q1.85 이라고 했으므로

     △P = 1.08 × 10-7 × Q1.85 × 40 [m] = 0.165 [MPa]

​

10. 어느소화배관내에 3 [m/s]의 유속으로 소화수가 흐르고있다. 마찰손실계수가 0.016, 배관길이가 1.000[m], 배관내경이

      100[m]일 때 배관의 조도를 구하시오. (단, 배관 마찰손실은 달시-웨버공식과 하젠 - 윌리엄스 공식을 이용하고 ,답은

      정수로 쓰시오.) [5점] ★★★★

[풀이] 조도(C)를 구하는 식은 하젠-윌리엄스식 밖에 없다.​

그런데 위식에서 조도(C)를 구할려면 압력변화와 유량을 구해야 한다. 압력변화를 알기 위해 달시-웨버식을 사용하게

 된다.

① 압력변화를 달시 - 웨버의 식으로 알아 보자.​

② 체적유량식을 이용하여 유량을 구해 보자.

     Q = A · v = π/4 · d2[㎡] × v [m/s] = π/4 × 0.12 × 3 × 60 = 1,380 [ℓ/min]

③ 하젠 - 윌리엄스식으로 조도(C)를 구해 보자.

11. 어느 수계 소화설비 배관 (일정한 관경)의 두 지점에서 압력계로 흐르는 물의 수압을 측정하였더니 각각 0.45 [MPa],

      0.4[MPa]이었다. 만약, 이 때의 유량 보다 1.5배 유량을 흘러 보냈다면 두 지점간의 수압차 [MPa]를 구하시오.

      (단, 배관의 마찰손실은 하젠 - 위리엄스 공식을 이용한다) [4점] ★★★★★

[풀이] ​

위식에서 상수 C, D, L은 같으므로 아래식으로 위식을 나누면 다음과 같다.​

[해설] 두 지점간의 수압차 : 하젠 - 윌리엄스 공식​

위 하젠 - 윌리엄스 식에서 압력변화는 유량에 비례하므로​

12. 직경 400[㎝]인 소화배관에 0.04[㎥/s]의 유량이 흐르고 있다가 ①, ②의 분기관으로 흐르다 다시 합쳐져 있다. 각 분기

      관에서의 관 마찰계수는 0.022라 할 때 ①,②의 유량 [㎥/s]을 계산하시오. (단, Darsy-Weisbach 식을 이용한다) [6점]

      ★★★★★

※ 최근 자주 출제

 ※ 병렬관로

  Q = Q1 + Q2

      = A1 · v1 + A2 · v2

  ※ Q1, Q2의 마찰손실수두는 동일하다.

  ※ 문제에서 제시한 조건에 따라 달시-바이스바흐식과 하젠-윌리엄스식을 적용한다.

[풀이] 달시 - 웨버식​​

위 식을 속도 v에 대하여 정리를 하면

위에서 산출한 값을 체적유량 공식에 대입을 하면​

13. 다음 그림은 어느 배관 평면도이며, 화살표 방향으로 물이 흐르고 있다. 배관 ABCD 및 AEFD 간을 흐르는 유량 [ℓ/min]

     을 각각 계산하시오. (단, 주어진 조건을 참조하시오)  [8점] ★★★★★

[조건]

① 하젠-윌리엄스의 공식은 다음과 같다.​

(단, △P : 배관의 길이 1[m]당 마찰손실압력 [MPa],

       Q : 유량 [ℓ/min], D : 관의 안지름 [㎜] )

  ② 호칭 50[㎜] 배관의 안지름은 54 [㎜] 이다.

  ③ 호칭 50 [㎜] 엘보 (90˚)의 등가길이는 1.6 [m]이다.

  ④ A 및 D점에 있는 티(Tee)의 마찰손실은 무시한다.

  ⑤ 루프(Loop) 배관 BCFEB의 호칭구경은 50 [㎜] 이다.

[풀이] L1 (ABCD) : 8 +10 + 6 + (1.6 ×2) = 27.2 [m]

          L1 (AEFD) : 2 +10 + 4 + (1.6 ×2) = 19.2 [m]

※ 마찰손실압력 △P(ABCD) = △P(AEFD) 이므로​

여기서, △P : 마찰압력손실 [MPa]

             Q : 유량 [ℓ/min]

             C : 관의 조도 [100]

             D : 관의 내경 [㎜]

             L : 등가길이 [m]

  ※ 등가길이를 적용할 것

   ① 배관 AECD 유량

     ▣ 병렬관로에서 문제 그림의 관로상 ABCD 방향과 AEFD 방향의 배관마찰손실은 같다.

         ∴ △P (ABCD) = △ P (AEFD)​​

         상수, C(100), D는 동일하므로 양변을 이들 수로 양분을 하면

         L1 · Q12 = L2 · Q22 이 된다.

  ⊙ L1(ABCD) = 8 + 10 + 6 + (1.6 × 엘보 2개) = 27.2 [m]

  ⊙ L2(AEFD) = 2 + 10 + 4 + (1.6 × 엘보 2개) = 19.2 [m]​

② 배관 AEFD의 유량

    Q = Q1 + Q2 에서 Q1 = Q - Q2 이므로

    Q1 = 500 [ℓ/min] - 271.74 [ℓ/min] = 228.26 [ℓ/min]

​

14. 다음 그림과 같은 어느 배관에서 화살표 방향으로 물이 흐르고 있다. 주어진 조건을 참고하여 Q1과 Q2 의 유량을 각각

       구하시오. [8점] ★★★★★

[조건] ① 하젠 - 윌리엄스의 공식은 다음과 같다.​

여기서, △P : 마찰압력손실 [MPa/m]

             Q : 유량 [ℓ/min]

             C : 관의 조도

             D : 관의 내경 [㎜]

             L : 등가길이 [m

  ② 호칭 25 [㎜] 배관의 안지름은 27 [㎜]이다.

  ③ 호칭 25 [㎜] 엘보 (90˚)의 등가길이는 1 [m] 이다.

  ④ 배관은 아연도금 강관을 사용한다.

  ⑤ ⓐ점, ⓑ점에 있는 티(Tee)의 마찰손실은 무시한다.

  ⑥ 배관내에 흐르는 유량은 200 [ℓ/min]이다.

  ⑦ 배관의 각 구간의 길이는 다음과 같다.

     ⓐ - ① : 3 [m] , ① - ② : 10 [m] , ② - ⓑ : 2 [m]

     ⓐ - ③ : 6 [m] , ③ - ④ : 10 [m] , ④ - ⓑ : 7 [m]

​

  가. 배관의 구간 (ⓐ-①-②-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

  나. 배관의 구간 (ⓐ-③-④-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

    [풀이]

 가. 배관의 구간 (ⓐ-①-②-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

   L1 (ⓐ,①,②,ⓑ) : 3 + 10 + 2 + (1×2) = 17 [m]

   L2 (ⓐ,③,④,ⓑ) : 6 + 10 + 7 + (1×2) = 25 [m]​

나. 배관의 구간 (ⓐ-③-④-ⓑ) 인 유량 Q1 [ℓ/min]을 구하시오.

     Q2 = Q - Q1 = 200 [ℓ/min] - 110.44 [ℓ/min] = 89.56 [ℓ/min]

​

[해설]

가. 전체 배관 유량

    Q = Q1 + Q 2

     여기서, Q : 전체 관로 유량

                  Q1 : 병렬관로 유량

                  Q2 : 병렬관로 유량

나. 하젠 - 윌리엄스식​

여기서, △P : 마찰압력손실 [MPa]

             Q : 유량 [ℓ/min]

             C : 관의 조도

             D : 관의 내경 [㎜]

             L : 등가길이 [m]

   ※ 등가길이를 적용할 것

    ① 배관 ⓐ①②ⓑ 유량

      ▣ 병렬관로에서 문제의 관로상 ⓐ①②ⓑ 방향과 ⓐ③④ⓑ 방향의 배관마찰손실은 같다.

        ∴ △P (ⓐ①②ⓑ) = △ P (ⓐ③④ⓑ)​​

상수, C, D는 동일하므로 양변을 이들 수로 양분을 하면

          L1 · Q11.85 = L2 · Q21.85 이 된다.

  ⊙ L1(ⓐ①②ⓑ) = 3 + 10 + 2 + (1 × 엘보 2개) = 17 [m]

  ⊙ L2(ⓐ③④ⓑ) = 6 + 10 + 7 + (1 × 엘보 2개) = 25 [m]​

 ② 배관 ⓐ③④ⓑ의 유량

    Q = Q1 + Q2 에서 Q2 = Q - Q1 이므로

    Q2 = 200 [ℓ/min] - 110.44 [ℓ/min] = 89.56 [ℓ/min]

​

15. 다음 그림과 같은 배관을 통하여 흐르고 있는 유량이 80[ℓ/s]이다. B,C관의 마찰손실 수두는 4[m]이고 B관의 유량은 20

      [ℓ/s]일 때 C관의 내경 [㎜]를 구하시오.  (단, 하젠-윌리엄스의 공식은​

   △P는 압력차 [MPa], L은 배관의 길이 [m], Q는 유량 [ℓ/min], C(조도계수)는 120, D는 내경 [㎜] 이다. [6점] ★★★★

[풀이] C관의 유량 : 80 [ℓ/s] - 20 [ℓ/s] = 60 [ℓ/s] × 60 [s] = 3,600 [ℓ/min]

          마찰손실수두의 압력변환​

#레이놀즈 #베르누이 #달시웨버 #하젠윌리엄스 #압력수두 #에너지보존법칙 #연속방정식 #중력가속도 #속도계수 #유량계수 #속도수두 #위치에너지 #표준대기압 #마찰손실계수 #병렬관로 #표준대기압 #압력수두

1. 다음 그림을 보고 각 물음에 답하시오. [8점] ★★★★★

  [조건]

   ① PA : 12.1 [kPa]

   ② PB : 11.5 [kPa]

   ③ PC : 10.3 [kPa]

   ④ 유량 : 5 [ℓ/s]

 (1) A지점의 유속 [m/s]을 구하시오.

 (2) C지점의 유속 [m/s]을 구하시오.

 (3) A지점과 B지점간의 마찰손실 [m]를 구하시오.

 (4) A지점과 C지점간의 마찰손실 [m]를 구하시오.

[풀이]

 (1) A지점의 유속 [m/s]을 구하시오.​

 (2) C지점의 유속 [m/s]을 구하시오.​

 (3) A지점과 B지점간의 마찰손실 [m]를 구하시오.

(4) A지점과 C지점간의 마찰손실 [m]를 구하시오.​

[해설] 베르누이 방정식

① 베르누이 방정식​

여기서, H : 전수두 (전양정) [m]

             P1, P2 : 압력 [Pa = N/㎡]

             γ : 물의 비중량 [9.8 kN / ㎥]

             v1, v2 : 유속 [m/s]

             g : 중력가속도 (9.8 [m/s2]

             Z1, Z2 : 위치 수두 [m]

            △H : 마찰손실수두 [m]

  ② 유량

           Q = A · v = π/4 · d2 · v

          여기서, Q : 유량 [㎥/s]

                       A : 배관의 단면적 [㎡] = π/4 · d2 [㎡]

                       v : 유속 [m/s]

                       d : 내경(안지름) [m]

​

2. 스프링클러 설비의 가압 송수장치에 대한 성능시험을 하기 위하여 오리피스로 시험한 결과 수은주의 높이가 500[㎜]로

     측정되었다. 이 오리피스를 통과하는 유량 [m/s]을 구하시오. (단, 수은의 비중은 13.6, 속도계수는 0.97 이고 중력가속

     도는 9.8 [m/s2] 이다.  [4점] ★★★★

[풀이]​

[해설] 벤츄리 미터 유량​

여기서, Q : 유량 [㎥/s]

             Cv : 속도계수

              A : 배관의 단면적 [㎡] = π/4 · d2 [㎡]

              A1, A2 : 내경 [m]

              g : 중력가속도 (9.8 [m/s2]

              γ2 : 수은의 비중량 (13.6 × 9.8 [kN/㎥]=133.28 [kN/㎥]=133,280[N/㎥]

              γ1 : 물의 비중량 (9.8 [kN/㎥]=9,800[N/㎥]

             △H : 수은의 높이차 [m]

3. 펌프성능시험을 하기 위하여 오리피스로 시험한 결과 수은주의 높이가 47[m]로 측정되었다. 이 오리피스를 통과한 유량

     [ℓ/s]을 구하시오. (단, 속도계수는 0.9이고, 수은의 비중은 13.6, 중력가속도는 9.81 [m/s]이다. [5점] ★★★

[풀이]​

[풀이]​

[해설] 벤츄리미터 유속​

여기서, v : 유속 [m/s]

            Cv : 속도계수

            d1, d2 : 내경 [m]

            g : 중력가속도 (9.8, 9.81 [m/s2])

             γ1 : 물의 비중량 (γ = ρ·g, 1,000[N·s2/m4] × 9.81[m/s2] = 9,810[N/㎥] = 9.81[kN/㎥]

            γ2 : 수은의 비중량 (13.6×9.81[kN/㎥]=133.416 [kN/㎥]=133,416[N/㎥]

            △H : 수은의 높이 차 [m]

  ※ 수은의 높이차가 주어지지 않고 A1과 A2의 압력이 주어진 경우​

[풀이]

[해설] 피토정압관의 유속​

여기서, v : 유속 [m/s]

            C : 유량계수

           △H : 수은의 높이 차 [m]

            g : 중력가속도 (9.8, 9.81 [m/s2])

            γw : 물의 비중량 (γ = ρ·g, 1,000[N·s2/m4] × 9.8[m/s2] = 9,800[N/㎥] = 9.8[kN/㎥]

             γ : 수은의 비중량 (13.6×9.8[kN/㎥]=133.28 [kN/㎥]=133,280[N/㎥]

             S : 수은의 비중 (13.6)

             Sw : 물의 비중 (1)

6. 그림과 같은 직육면체(바닥면적 6m × 6m)의 물탱크에서 밸브를 완전히 개방하였을 때 최저 유효수면까지 물이 배수되

      는 소요시간 [min]을 구하시오. (단, 토출측 관 안지름은 80 [㎜]이고 탱크 수면 하강속도가 변화하는 점을 고려할 것)

      [4점] ★★★

[풀이] ※ 유량계수가 주어지지 않았으므로 대입하지 않음​

[해설] 물의 배수시간​

여기서, t : 배수시간 [s]

            At : 물탱크의 바닥면적 [㎡]

            A : 배관의 단면적 [㎡] = π/4 · d2 [㎡]

            g : 중력 가속도 (9.8 [m/s2])

           H1 : 물탱크내 최고 수위 [m]

           H2 : 물탱크내 최저수위 [m]

            d : 내경(안지름) [m]

​

7. 스프링클러설비에 사용되는 관의 내경이 35[㎜]인 수평배관의 유량이 100[ℓ/s]이다.

     이 때, 배관내 압력 [kPa]을 구하시오. (단, 중력가속도는 9.8 [m/s]이다) [4점] ★★​

※ 계산기 Slove 기능 활용 ​

8. 어떤 공장의 배관 시스템으로서 물의 유속이 20 [m/s], 압력이 300[kPa], 온도가 20 [℃]로 대퓨저에 유입하여 유속

    5 [m/s]으로 유출되었다면 이 물의 유출압력을 구하시오. (단, 위치관계는 무시하고 비체적은 0.001001 [㎥/㎏]이다. [3점]

     ★

※ 비체적 = 1/밀도, Vs = 1/ρ, ρ =1/Vs​

[베르누이 방정식]​

여기서, H : 전수두 (전양정) [m]

             P1, P2 : 압력 [Pa = N/㎡]

             γ : 물의 비중량 9.8 [kN / ㎥]

             v1, v2 : 유속 [m/s]

             g : 중력가속도 (9.8 [m/s2]

             Z1, Z2 : 위치 수두 [m]

9. 다음 그림과 같이 관에 중량유량이 9,800[N/min]으로 40[℃]의 물이 흐르고 있다. ② 점에서 공동현상이 일어나지 않을

    ①점에서의 최소압력 [kPa]을 구하시오. (단, 배관의 손실은 무시하고 40[℃] 물의 증기압은 55.324[㎜Hg]이며, 소수점

    다섯째 자리까지 구하시오. [5점] ★★★★★

[풀이]​

[해설] 공동현상, 베르누이 방정식

가. 베르누이 방정식​

여기서, P1, P2 : 압력 [Pa = N/㎡]

             γ : 물의 비중량 [9.8 kN / ㎥]

             v1, v2 : 유속 [m/s]

             g : 중력가속도 (9.8 [m/s2]

            Z1, Z2 : 위치 수두 [m]

  나. 중량유량

     ⊙ 중량유량 G = γ A1·v1 = γ · A2 · v2 [N/s]

         여기서, G : 중량유량 [N/s]

                      A1, A2 : 배관의 단면적 [㎡] = π/4 · d2 [㎡]

                      v1, v2 : 유속 [m/s]

                      γ : 물의 비중량 (γ = ρ·g, 1,000[N·s2/m4] × 9.8[m/s2] = 9,800[N/㎥] = 9.8[kN/㎥]

                       d : 내경 (직경) [m]

​

#비중량 #밀도 #베르누이 #중력가속도 #벤츄리 #토리첼리 #피토정압관 #유량계수

#스프링클러 #오리피스 #속도계수 #체적유량 #질량유량 #중력가속도 #압력 #유속

1. 펌프의 흡입이론에서 볼 때 물을 흡입할 수 있는 이론 최대 높이 [m]를 구하시오. (단, 대기압은 760 [㎜Hg], 수은의 비중

     량은 133,280[N/㎥], 물의 비중량은 9,800[N/㎥]이다) [4점] ★★★★

[풀이]​

[해설] 이론 최대 높이 (이론 흡입 수두 (양정))

          P = γ1·H1 = γ2 · H2 [Pa = N/㎡]

          여기서, P : 압력 [Pa = N/㎡]

                       γ1 : 수은의 비중량 (133,280[N/㎡] = 133.28 [kN/㎡])

                       H1 : 수은의 높이 (수두) [m]

                       γ2 : 물의 비중량 (9,800 [ N/㎡] = 9.8 [kN/㎡])

                       H2 : 물의 높이 (수두) [m]

​

[관련 문제] 옥외소화전의 전동력을 구하시오.

   ① 옥외소화전은 5개 설치되었다.

   ② 실양정은 20 [m] 이다.

   ③ 호스길이는 25 [m] 이다. (호스 마찰손실 수두는 호스길이 100[m]당 4[m]이다)

   ④ 배관 및 배관의 마찰손실수두 : 10 [m]이다.

   ⑤ 펌프의 효율 50은 [%] 이고 전달계수는 1.1 이다.

   ⑥ 관창에서의 방수압은 : 29 [mAq]이다.

   ⑦ 주어진 조건외에는 다른 값은 무시한다.

[문제풀이]​

   방수량 Q : 옥외 소화전 350 [ℓ/min]의 최대 2개 까지 적용하므로 350 [ℓ/min] × 2 = 700 [ℓ/min] = 0.7 [㎥/min]

   전양정 H = h1 + h2 + h3 + 25 [m]

    여기서, H : 전양정 [m]

                 h1 : 소방호스의 마찰손실수두 [m]

                 h2 : 배관 및 관부속품의 마찰손실수두 [m]

                 h3 : 실양정 (흡입양정 + 토출양정) [m]

                 25 : 옥외소화전설비 규정방수 압력의 환산수두 [m] (0.25 [MPa] ⇒ 25[m])

                  ∴ H = 25 × (4/100) +10 + 20 + 29 = 60 [m]​

[관련 문제 2] 송풍기의 동력 [kW]을 구하시오.

   ⊙ 총 누설량 : 2.1 [㎥/s]

   ⊙ 총 보충량 : 0.75 [㎥/s]

   ⊙ 송풍기의 효율 : 50 [%]

   ⊙ 송풍기의 압력 : 1,000 [Pa]

   ⊙ 전달계수 : 1.1

   ⊙ 송풍기 풍량의 여유율 : 15 [%]

[풀이]​

   풍량 Q = (총 누설량 + 총 보충량) × 여유율 = (2.1+0.75) × 1.15 = 3.227 [㎥/s]​

2. 제연설비의 공기 유입 덕트내에 분당 180 [㎥]의 공기가 유입될 때 그림 "A, B, C" 각 부분에서의 이론 공기 유속 [m/s]을

      구하시오. (단, 덕트내의 마찰손실은 무시한다) [6점] ★★★★★

   단면적 : A = 120 × 70 [㎠]

                B = 120 × 60 [㎠]

                C = 120 × 50 [㎠]​

3. 그림과 같이 배관을 통하여 할론 1301의 정상흐름(steady flow)이 일어나고 있다. 이 흐름이 1차원 유동이라고 할 때 ②

    지점에서의 할론 1301의 밀도 [g/㎥]를 구하시오. (단, ①, ② 지점에서의 내부 단면적의 직경은 50[㎜]와 25[㎜]이다.

    [4점] ★★★★★

  [풀이]

   질량유량 M = ρ1 · A1 · v1 = ρ2 · A2 · V2 [㎏/㎥]​

4. 온도 20 [℃], 압력 196.14 [kPa]인 공기가 안지름 150 [㎜]인 배관을 1.5 [㎏/s]로 유동하고 있다. 유동을 균일 분포 유동으

    로 가정할 때, 유속 [m/s]을 구하시오. (단, 공기의 기체상수 R = 0.287 [kJ/㎏·K]로 한다. [4점] ★★★

[풀이]​

5. 물이 매초 당 3,00 [N]으로 내경 300[㎜]인 소화배관을 통하여 흐르고 있다. 다음 각 물음에 답하시오. [5점] ★★★★★

  (1) 소화배관내 물의 평균 유속 [m/s]을 구하시오.

  (2) 소화배관 내 물의 평균유속을 9.7 [m/s]으로 할 경우 소화배관의 관경 [m]을 구하시오.

[풀이]​

  (2) 계산기의 Solve 기능을 활용하여 풀어 보자.​

6. 내경이 80[㎜]인 옥내 소화전 설비의 배관에 유량이 390 [ℓ/min]으로 흐르고 있다. 

    다음 각 물음에 답하시오. [6점] ★★★★★

  (1) 배관내의 평균유속 [m/s]을 구하시오.

  (2) 질량 유량 [㎏/s]을 구하시오.

  (3) 중량 유량 [N/s]을 구하시오.​

7. 옥내 소화전 방수구에 직경 15[㎜]의 오리피스를 설치하였다. 압력이 0.5[MPa]일 경우 방수량 [ℓ/min] 은 얼마인가 ? (단,

    오리피스 계수는 0.75 이다) [6점] ★★★​

※ 유량계수(오리피스계수, 흐름계수 등)이 주어지면 2.086 ÷ 0.99 = 2.107 값을 적용, 이 때 C = 0.99

     2.086은 유량계수가 적용된 값이다.

     2.107은 유량계수가 적용되지 않은 값이다.

     유량계수 값이 주어지면 2.107값을 적용하고 그렇지 않으면 2.086를 적용한다.

       ⊙ 유량계수값이 주어지지 않을 경우 : 2.086

       ⊙ 유량계수값이 주어지는 경우 : 2.107

[관경을 구할 때]​

   ※ 방수량 산정식​

   여기서, Q : 방수량 [ℓ/min]

               C : 흐름계수 (유량계수, 오리피스 계수)

               D : 구경(직경) [㎜]

                  - 노즐구경 : 옥내소화전설비 : 13 [㎜]

                                      옥외 소화전 설비 : 19 [㎜]

               P : 방수압 [MPa]

​

#방수압 #체적유량 #질량유량 #중량유량 #흡입양정 #실양정 #비중량 #밀도 #마찰손실

#양정 #수두 #제연설비 #소화전