보어의 원자 모형부터 "양자수"라는 개념이
가볍게 등장하게 되는데 이 부분을 이해하는데 있어
수험생들이 많이들 어려움을 겪게 되지요.
이번 포스팅에서는 보어의 원자 모형과 양자수라는
개념을 연관지어 정리해보는 시간을 갖겠습니다.
[목차]
1. 러더퍼드 원자 모형의 한계점.
2. 양자화란?
3. 보어의 원자 모형과 주 양자수.
4. 주 양자수(n)는 어떻게 정해질까?
러더퍼드 원자 모형의 한계
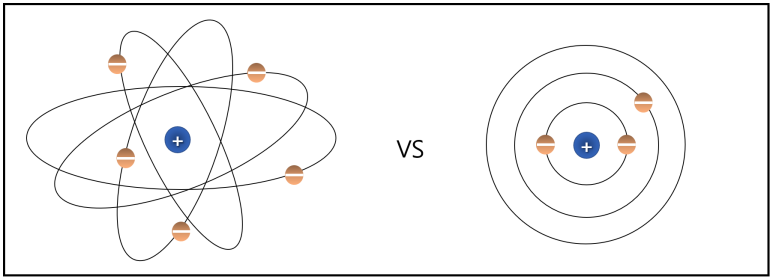
러더퍼드 모형 보어의 원자 모형
러더퍼드가 제안한 원자 모형과 보어의 모형에서
가장 두드러진 차이점은 전자의 궤도입니다.
과거 러더퍼드 모형에서 전자는 특정한 궤도가 없이
무작위로 돌고 있는 형태를 보이고 있습니다.
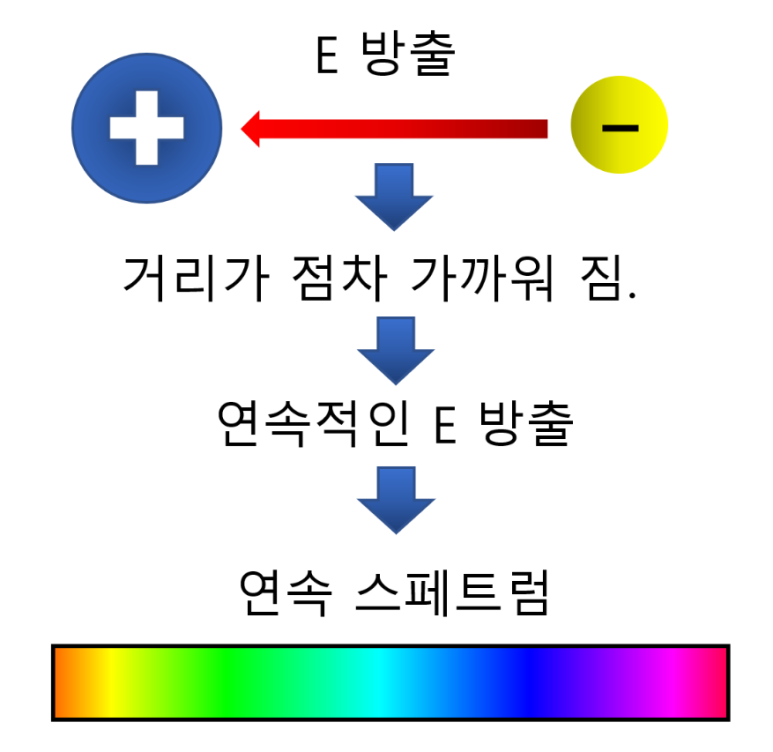
전자가 원자핵 주위를 무작위로 돌고 있다는 것은
시간이 지날수록 전자가 에너지를 잃게되며
원자핵에 점점 가까워져 소실된다는 것이지요.
(핵(+)과 전자(-)의 인력 작용)
거리가 점점 가까워진다는 것은
연속적으로 가까워진다는 것이므로,
연속된 에너지(E)가 방출 됨.
하지만, 실제 수소 원자의 스펙트럼을 보면
연속적이지 않은 "불연속 선 스펙트럼"의
형태를 보이게 됩니다.

수소 원자의 선 스펙트럼
원자는 연속적인게 아닌, 특정한 에너지 값만
갖고 있는 다는 것이므로, 러더퍼드의 원자 모형은
한계를 보이게 되지요.
보어는 이러한 불 연속적인 특정한 에너지 값만 갖는
원자를 설명하기 위한 원자 모형을 제시하게 됩니다.
양자화란?
원자의 불연속적인 선 스펙트럼을 설명하기 위해서
과학자들은 양자화라는 개념을 도입했습니다.
양자화라는 것은 간단히 말해서
원자가 갖는 에너지(E)는 연속적이지 않으므로,
모든 에너지는 "정수배"의 수식으로 나타내어
에너지값을 해석해 보겠다는 뜻입니다.
이러한 "정수배"의 관계로 E 값을 구하기 위해
나타내는 필요한 수식들을 "양자수"라고 합니다.
(ex.) 주 양자수(n)=1, 2, 3, 4...)
E 값을 모두 정수배로 해석하기 때문에
이러한 양자수들은 정수값을 갖게 됩니다.
[정리]
원자의 에너지는 연속적이지 않음.
↓
불연속적인 에너지 값을 갖음.
↓
에너지(E)를 정수배(양자화)로 해석.
↓
양자수(정수값)와 관련된 수식을 이용해 E 값을 구함.
보어의 원자모형과 주 양자수(n)
보어는 러더퍼드 모형의 한계점과
불연속 선 스펙트럼을 설명하기 위한
새로운 원자 모형을 제안합니다.
※보어의 모형은 "수소 원자"를 기반으로 설명함※
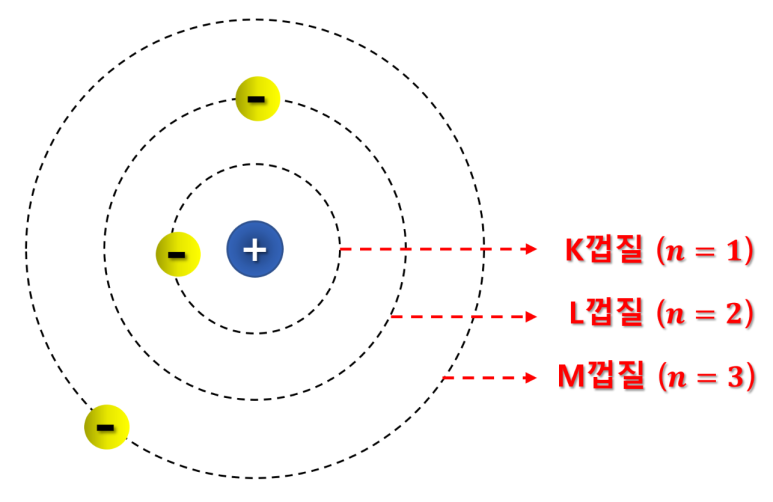
보어의 원자모형
보어는 전자가 에너지(E)를 잃지 않는
특정 궤도만을 돌고 있고,
각 궤도는 원자핵에 가까운 순서부터
K, L, M, N... 껍질이라 정의합니다.
각 껍질(궤도)에 존재하는 전자의 에너지(E)는
껍질마다 해당하는 "주 양자수(n) 값"에 의해
결정이 되는 것이지요.
(ex. K껍질 : n=1, L껍질 : n=2...)
여기서, 주 양자수는 1, 2, 3, 4의 정수값을 갖고
실제로 각 궤도의 전자가 갖는 에너지는
주 양자수와 관련된 에너지 값을 갖는다는 것을
알게 됩니다.
[각 껍질에서 수소전자의 에너지 준위]
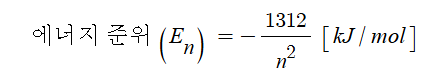
K껍질(n=1) : E1 = - 1312 / 12 kJ / mol
L껍질(n=2) : E2 = -1312 / 22 kJ / mol
M껍질(n=3) : E3 = -1312 / 32 kJ / mol
…
그렇다면, 도대체 에너지 준위를 구해주는
주 양자수(n)란 어떻게 나온 것일까..?
주 양자수(n)는 어떻게 정해질까?
전자는 입자와 "파동"의 성질을 갖는다.
사실, 양자수는 이해하기에 꽤나 난해한 이론입니다.
대략적인 틀만 이해해보면 다음과 같습니다.
과학자들은 "이중슬릿 실험"을 통해
전자는 입자와 파동의 성질을 모두 갖는다는 것을
발견했습니다.
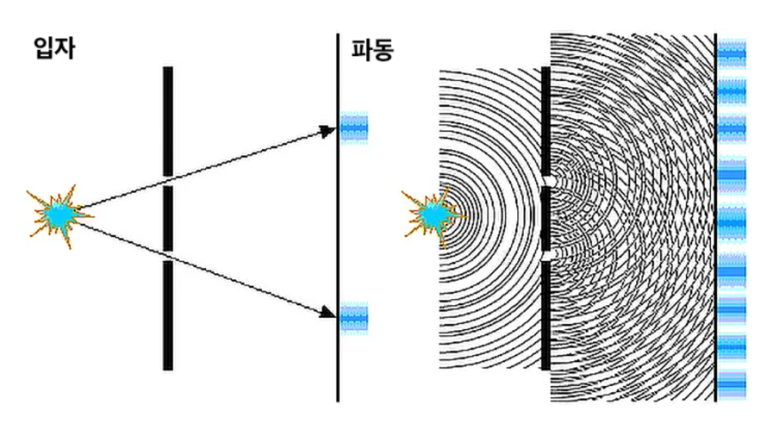
출처 : 나무위키
각 궤도의 불연속적인 에너지(E) 값을 나타내는
주 양자수(n)는 이러한 전자의 파동의 성질에
기반하여 나온 정수입니다.
드브로이라는 학자는 전자가 입자와 파동의 성질을
갖는다고 가정하고, 입자라고만 생각했던 전자가 파동의
특성을 보일수 있음을 수학적으로 유도해냅니다.
이것을 드브로이의 "물질파"라고 부르게 되지요.
이 "물질파"를 바탕으로 보어의 원자 모형에서
에너지를 잃지 않는 특정 궤도를 간단히 설명하면
다음과 같습니다.
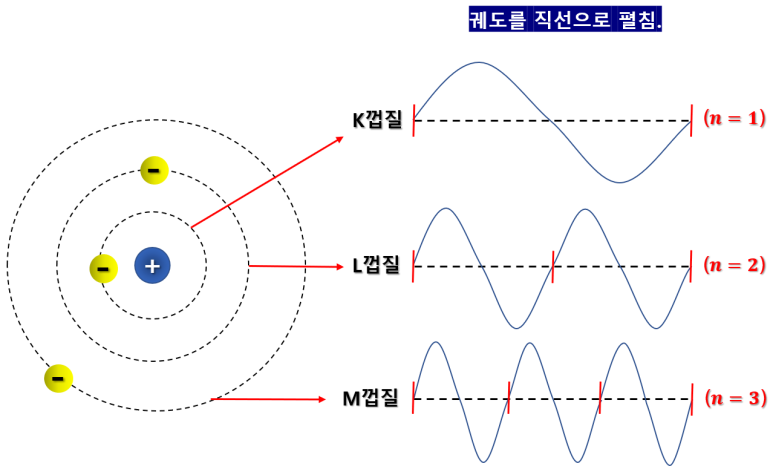
전자의 각 궤도와 파동의 관계
그림과 같이 각 궤도에서 파장이 정확히 정수배로
끊기는 부분에 전자가 존재해야 에너지를 잃지 않고
궤도를 유지할 수 있다는 것이지요.
그림과 같이 각 껍질에서 궤도의 길이가
파장의 길이의 1배 일 때, n=1
파장의 길이가 2배 일 때, n=2
파장의 길이가 3배 일 때, n=3
의 관계 정도로 해석하면 좋을 듯 합니다.
(이해를 돕기위한 간략한 설명일 뿐입니다.)
다른 궤도에 전자가 존재한다면..?
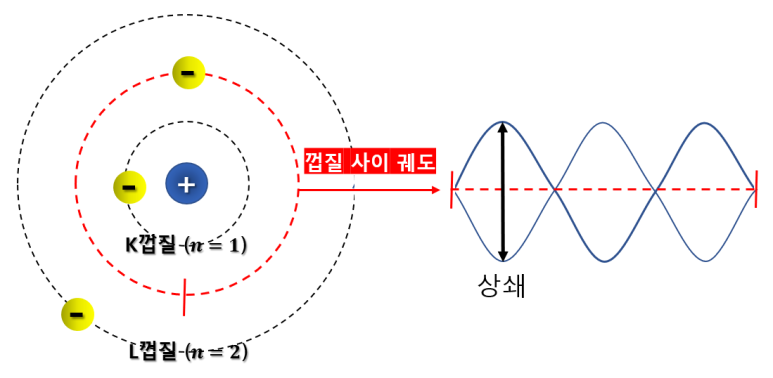
다른 궤도에 전자가 존재할 경우.
위와 같은 궤도 외에 전자가 존재하게 된다면
파장의 길이가 궤도와 정수배에 해당하지 않으므로,
파장의 시작점과 궤도의 시작점이 일치하지 않게되어
다음 파동에서 상쇄가 일어나기 때문에 전자는
에너지를 잃고 존재하지 않게 됩니다.
따라서,
각 궤도의 전자가 갖는 에너지 준위를
주 양자수(n)를 이용해 에너지(E)값을 구할 수 있고,
이러한 에너지(E)를 불연속 값(정수배, 주 양자수)
으로 설명할 수있게 되는 것이지요.
#양자수 #에너지궤도 #보어 #원자모형
'위험물 기능장 > 일반화학및유체역학' 카테고리의 다른 글
| 위험물의 분류 및 지정수량 (0) | 2025.01.29 |
|---|---|
| 위험물의 명명법 (2) | 2025.01.26 |
| 혼성 오비탈 (Hybrid Orbital) (2) | 2024.12.26 |
| 화학결합 - 공명구조, 형식전하, 옥텍규칙 예외, 확장 (0) | 2024.12.24 |
| 공유결합, 원자가결합이론 (VBT)의 한계 (0) | 2024.12.24 |
