아낌없이 주는 나무

1. 질량중심

▣ 질량중심 (質量中心) 은 물체 전체의 질량의 중심점으로 전체 질량이 질량 중심에 있는 것처럼 외부 계와 작용한다.

    미분질량의 위치를 질량가중치(미분질량/전체질량)를 곱하여 적분한 것이다. 중력이 균일한 경우 무게 중심과 같기

    때문에 혼용하기도 한다.  이 때 물체의 각 부분에 작용하는 중력를 합한 합력의 작용점을 무게 중심이라고 한다.

​

2. 직선에 놓인 점들의 질량 중심

아래 그림과 같이 지렛대가 놓은 받침점을 원점으로 하여 좌표 xk인 점에 질량 mk가 놓여 다고 가정하자. (k = 1,2,3)

각 질량 mk에 아래 쪽으로 중력이 작용한다. 중력가속도 g가 작용하여 원점을 중심으로 회전하려는 힘이 생긴다.

이 힘을 토크(toque)로 부르는데 크기는 gmk이고 부호는 위치 xk에 따라 결정된다. 양(+)이면 시계방향으로 음(-)이면

반시계 방향으로 회전하는 힘이 작용한다. 토크를 모두 더한 값이 시스템 토크다.  (참고 토크 τ는 변위 벡터 r과 힘 F의

외적이다. τ = r × F 이다. 따라서 편하기 다루기 위해  '+'는 반시 계방향, '-'는 시계방향인 오른손 법칙을 따라 방향을 정한다)

시스템 토크가 0이면 어느 쪽으로도 기울지 않는다. 시스템은 균형을 이룬다. 시스템 토크를 다시 정리하면 아래와 같다.​

여기서 중력가속도 g는 시스템의 환경에 따라 달라진다. 지구라면 중력가속도 9.8 [m/sec2) 이지만 다른 천체라도면 달라

질 것이다. 하지만 중력가속도를 제외한 m1x1+ m2x2 + m3x3는 환경에 영향이 없이 어디서든 똑같다. 이 값을 원점에

대한 모멘트 (moment of the system about the origin)이라고 하며 식으로는 다음과 같다.​

시스템이 균형을 이루는 점을 찾아 보자. 균형점 x바에 대한 토크는 질양 mk가 있는 위치 (xk-x')와 중력가속도의 곱이 토크

의 합이 0이 되어야 균형점이다.

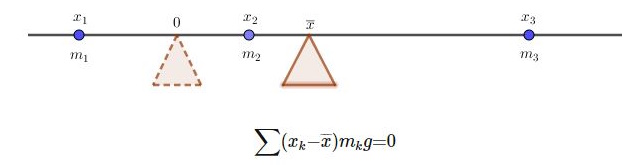
이 식을 x바에 대한 식으로 정리하면 다음과 같다.​

위 식에서는 질량이 질량중심에 집중되어 있다면 그것의 모멘트는 전체 모멘트의 합과 같음을 의미한다. 이는 질량이

균일할 경우인데 만약 질량이 균일하지 않으면 밀도가 함수로 주어질 것이고 함수를 적용하여 계산하게 된다.

밀도 = 질량 / 길이(체적)을 말한다. 따라서 질량은 밀도 × 길이가 된다. 즉, △mk = δ(x) × △xk가 된다. 따라서 질량중심을

밀도로 나타낸 다면 다음과 같이 나타낼 수 있다.​

3. 평면에 놓인 질량중심

​

평면 위에 작용하는 질량 중심을 알아 보기 위해서는 먼저 면적을 선의 개념으로 변환하는 것이 필요하다. 면적을 선개념

으로 변환하기 위해서는 미분을 해야 하는데 여기서는 미분방법 보다는 x축, y축을 기준으로 하여 모멘트를 구하는 방식을

취한다. x축을 기준으로 한다는 말 속에는 x축을 미분하여 한 점으로 만든다는 의미와 같게 된다. 그 이유는 x축을 기준으

로 하는 모멘트 예를 들어 my1x1, my1x2, my1x3, my1x4 ··· my1xn은 모두 x축을 기준으로 하는 모멘트 같기 때문이다.

따라서 x축을 기준으로 한다고 하면 어떤 주어진 면을 y축으로 평행한 선으로 변형할 수 있게 된다. y축을 기준으로 할 때

에도 x축을 기준으로 할 때와 같다. 이를 바탕으로 면에 대한 질량 중심을 구할 수 있게 된다.

이제 면적에 대한 질량중심을 알아 보도록 하자.

평면위에 좌표 (xk,yk)인 점에 질량 mk가 놓여 있다고 하자. 즉, 이 평면은 질량이 일정한 균질의 평면이라고 하자.

이 때 이 평면의 전체 질량 M은 각각의 질량의 합이 될 것이고 x축과 y축에 대한 모멘트는 다음과 같은 식으로 표현할 수

있다.

또한 질량중심을 좌표 x바, y바라고 한다면 이는 다음 식으로 나타낼 수 있다.​

질량이 두께가 아주 얇고 평평한 판에 고르게 퍼져 있다고 가정하면 위에서 정리한 내용을 폭이 "0"에 아주 가까운 매우

가는 띠로 나누어 구하는 것으로 생각할 수 있다. 이는 x축을 미분하는 것으로 앞에서 말한 바와 같이 x축을 기준으로 하면

모멘트는 y축 방향으로 x으로 부터 떨어진 거리에 의해 영향을 받고 x축 방향으로 y축에서 떨어진 값 즉, x값에는 영향을

받지 않기 때문이다. 따라서 x축은 선전체를 한 점으로 생각해도 된다. 이제 y축에 평행한 직선으로 n등분하고 부분합을

구하고 이 부분합의 극한값을 구하는 것은 바로 정정적분으로 질량중심을 구하는 것이 된다.

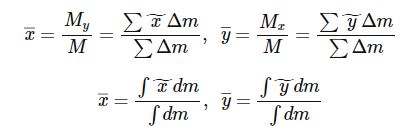
위 식에서 띠의 넓이를 A라고 하고 미분면적의 질량 dm 대신에 밀도 δ가 주어진다면 질량 dm 대신에 δdA를 대입하면

된다.

​

예제 : 세 직선 y = 2x, y = 0, x = 1로 둘러 쌓인 삼각형에 밀도 δ = 3g /㎠ 로 고르게 질량이 분포되어 있다고 할 때 질량중심

          을 구하여라.

위 그림과 같이 먼저 y축과 평행하고 폭이 dx인 띠를 생각하자. 이 때의 질량중심으로 (x출결, y물결)이라고 하면 띠의 면적 A는 미분면적으로 2xds가 되고 미분면적에 대한 질량은

미분밀도와 면적의 곱이 된다. 이를 이용하여 식을 전개하면 다음과 같다.​

질량중심 y 좌표도 x좌표와 동일한 방식으로 구할 수 있다.

#무게중심 #질량중심 #밀도 #질량 #적분 #미분 #모멘트 #평면 #직선

▣ 어떤 용기에 담겨있는 물의 압력이나 고인 물의 압력을 계산하는데는 정수압에 대한 관련식이 필요하다.

물에 의한 압력이 작용하는 사례는 우리 주변에 매우 많다. 위 그림은 미국 콜로라도의 후버댐과 우리나라 소양강댐의

사진이다. 이들 댐을 설계할 때는 정수압의 계산이 필요하다.

즉, 정수력, 유체의 수심에 따라 선형적으로 변동하는 유체의 압력 계산이 필요하다.

그런데 위 그림에서 소양강댐은 댐체가 직선이고 후버댐은 곡선이다. 따라서 수압이 소양강

댐은 평면에 작용하고 후버댐은 곡면에 작용한다. 평면과 곡면에 작용하는 수압을 측정하는 방법에 대하여 알아 보자.

수압의 영향을 받는 구조물은 댐 뿐만 아니라 하천에 설치하는 교각, 가물막이 막, 방파제,

교각설치를 위한 케이슨 등 다양하다.

​

먼저, 평면에 가해지는 정수력에 대해 알아 보자.

대표적인 형태로 소양강댐에 대해 살펴보자. 위 그림의 왼쪽 그림은 소양강댐 전경사진이고

오른쪽 그림은 개념적으로 댐의 단면을 보여주고 있다. 그림에서 댐체의 단면중 공기와 닿

는 부분을 제외한 수중 부분을 보면 댐체와 물을 평면으로 닿고 있음을 알 수 있다.

그런데 평면이냐 곡면이냐에 따라 수압이 댐체에 미치는 영향이 달라진다.

​

정수력은 어떤 면에 수직적으로 작용하는 단위 면적당 힘인데 이 때 입력은 위치에 따라

달라질 수 있기 때문에 수학적으로는 dF/dA에 대하여 극한값을 취하게 된다. 그렇다면

거꾸로 어떤 면에 작용하는 힘은 어떤 면에 작용하는 압력의 미분값을 적분하면 얻을 수

있다. 그런데 어떤 면에 압력이 균일하게 작용한다면 압력 P가 상수가 될 것이다.

이런 경우 작용하는 힘은 압력상수에 면적 곱하여 산정된다.

즉 F = PA로 나타낼 수 있다.

​

앞에서 어떤 면에서 균일하게 압력이 작용한다면 그 면에 작용하는 힘은 압력 × 면적으로

산정할 수 있다고 하였다. 그런데 힘은 벡터이므로 벡터적 관계에서 살펴보자.

위 그림의 왼쪽 그림을 보면 압력이 균일하게 작용한다고 하였으므로 압력 P는 상수가 되고

작용하는 힘은 P × A 가 되는데 힘은 벡터인데 P와 A는 스칼라값이므로 물의 압력에 대응

하는 힘을 산정하려면 압력과 반대방향으로 단위 벡터 n벡터를 추가해야 한다.

오른쪽 아래 그림을 보면 비어있는 십자원은 압력중심이고 유체의 하중을 받는 압력의 중심

을 말한다. 반면 센트로이드는 도심을 의미한다. 위쪽 압력은 균일하므로 압력중심과 도심

의 위치가 같다.

​

이번에는 균일한 압력이 평면이 아닌 곡면에 작용하는 경우를 알아 보자. 위 그림을 보면

비정형인 파란색의 물체가 있다고 하자. 위와같은 물체가 대기중에 있다고 하면 물체의 상

부 쪽 빨간색 화살표 쪽으로 대기압이 작용하게 된다. 물론 위치에 따라 대기압이 다르지만

물체가 크지 않다고 한다면 모든 위치에서 대기압이 같다고 하여도 무방하다. 그러면 이 물

체에 작용하는 힘을 구한다고 한다면 힘은 -nPdA를 적분하면 된다.

그런데 n벡터는 위치에 따라 방향이 바뀌게 되므로 적분할 때 상수로 취급할 수 없게 된다.

따라서 힘을 구하기 위해서는 적분을 해서 구해야 하는데 dA =rdθ 이고 n 벡터는

icosθ + jsinθ 가 된다. 이를 적분을 하면 합이 "0"이 된다.

​

위 그림 왼쪽을 보면 풍선의 내부압력은 풍선이 커지거나 작아지지 않으므로 대기압력과

평행을 이루고 있다고 할 수 있다. 즉 대기압과 같다고 할 수 있으므로 내부 압력은 계기압

력 "0"이 된다. 또한 오른 쪽 그림은 풍선에 작용하는 힘은 풍선에 수직방향으로 균일하게

작용하게 되므로 압력 P에 풍선의 단면적을 곱한 값이 될 것이다. 풍선의 단면적은 πr2이다.

아래 그림에서 물방울의 경우 대기압력과 물방울의 표면장력과 같은 경우와 같은 예라고

할 수 있다.

​

이제 본격적으로 평면에 작용하는 정수력의 크기를 산정하는 방법에 대해 알아 보자.

위 그림의 오른쪽은 소양강댐 사진이고 왼쪽 그림은 댐을 내부에서 바라본 것이라고 가정을

하면 댐체는 수직으로 서 있지 아니하고 경사면을 띠게 된다. 댐체의 면을 Y축이라고 하고

Y축과 수면이 만나는 점을 "O", 수면에서 하늘 쪽 수직방향이 "Z"이라고 하자. 또한 수면과

댐체면이 이루는 각도를 "α"라고 하자.

Y방향으로 작용하는 정수압은 위치에 따라 선형적으로 작용한다는 것을 알 수 있다.

깊이가 깊어지면 압력이 높아진다. 압력을 식으로 나타내면 압력 P = γysinθ라고 할 수 있

다. 여기서 γ 는 물의 단위 중량, 비중량이고 수심은 ysinα 가 된다. 댐체의 어떤 미소면적을

dA라고 하자. 미소면적에 작용하는 힘은 dF =PdA가 된다. 아주 작은 미소면적이므로

압력은 위치에 따라 변하지 않는다고 할 수 있으므로 압력 P'를 상수취급해도 된다.

이 때 P'를 기준으로 하중을 구하자. P'는 도심에 작용하는 압력이다. 작용하는 힘을 구하려

면 적분을 y 즉 도심까지 거리로 적분을 해야 하는데 도심에서의 압력으로 구할 수 있다.

즉, F = P'A로 구할 수 있다.

위 그림의 오른쪽 그림을 보면 노란색 선이 보이는데 이 노란색 단면이 우리가 구하고자 하

는 압력의 단면이다. 미소면적 dA이고 도심까지의 거리가 y, 도심의 압력을 P'라고 하자.

작용하는 힘은 압력 × dA를 적분하면 된다. 그런데 압력 P =γysinα라고 하였으므로

위의 식으로 정리할 수 있다. γsin θ 는 상수이므로 적분식에서 밖으로 나올 수 있으므로

결국 정리하면 F = P'A 가 된다.

​

#압력 #정수압 #벡터 #곡면 #평면 #방정식 #수압 #적분 #미분 #균일압력 #선형적

#소양강댐 #후버댐 #극한값 #상수