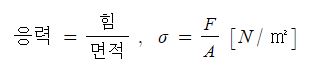1. 응력 (Stress, σ) 이란 ?
응력 (Stress, σ)은 외부로 부터 가해지는 힘 또는 압력에 의해 물질 또는 물체 내부에서 발생하는 내부력이나 압력을 나타내는 물리적인 양이다. 응력은 단위 면적당 내부 힘의 강도로 나타낸다. 응력은 단위 면적당 힘을 크기로 표현한다.
응력은 외부의 힘, 온도 변화, 변형 등 다양한 외부 요인에 의해 발생한다. 이에 대응하는 응력은 물질이 외부 영향에 대해 어떻게 반응하는지를 나타내 주기도 한다.
응력에는 다음과 같은 여러가지 유형이 있다.
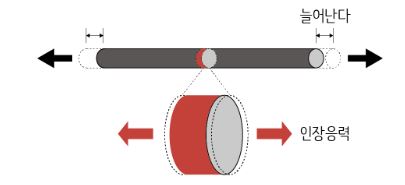
◈ 인장 응력 (Tensile stress) : 인장 응력은 물질을 늘리거나 길게 늘어나는 힘이 작용했을 때 나타난다. 물질의 길이 방향
으로 인장이 발생하며 양(+)의 응력값을 가진다.
◈ 압축 응력 (Compressive stress) : 압력 응력은 물질을 압축하거나 압착할 때 발생한다. 물질의 길이 방향에서 압축이
발생하며 음(-)의 응력값을 가진다.
◈ 전단 응력 (Shear stress) : 굽힘 응력은 굽힘 또는 휨 하중에 의해 인장 및 압축 응력이 복합적으로 작용하는 물체에
발생한다. 물체의 볼록(인장) 및 오목 (압축) 면에서 발생한다.
응력을 이해하는 것은 공학, 재료과학, 그리고 다양한 분야에서 구성요소, 구조물, 재료의 구조적 무결성, 성능, 안정성을 보장하기 위해 중요시 된다. 응력 분석을 통해 응력 분포와 그 영향을 평가하여 구조물과 재료를 설계, 평가, 최적화하고 안전한 한계 내에서 운영할 수 있도록 결정을 내릴 수 있다.
응력 (σ)은 힘(F)를 면적 (A)로 나눈 값으로 표현한다.


위 그림과 같이 막대가 바닥에 고정되어 있고 그 위로 당기는 힘이 작용한다고 하자. 외력 (External force)는 Fe라고 하고 이에 대응하여 물체를 지지하기 위한 반력(Reaction Force)를 Fr 이라고 하면 두 힘의 크기는 같게 된다.
위 그림의 오른 쪽 부분은 막대의 일부분을 나타낸 것이다. 응력 (Stress)이란 단위 면적당 물체가 원래 형태로 돌아 가려고 하는 저항력을 말한다. 위, 오른쪽 그림과 같이 막대기의 절단면을 따로 떼어내 살펴보면 외력에 의해 동일한 힘 Fs 로 원래 상태로 되돌리려는 복원력이 생기게 된다. 즉, 이 힘은 변형시키려는 힘에 대응하여 견디려고 하는 힘인 내력이 된다. 정지된 상태를 유지하기 위한 내력 Fi가 동일하게 작용하게 된다. 이를 아래와 같이 표현할 수 있다.
∑ 응력 = 내력
2. 응력 (Stress, σ)의 측정 및 사용 목적
응력 (σ) 값은 다양한 분야에서 사용되며 해당 분야에 따라 다양한 분석과 응용이 이루어 진다.
Structural Engineering and Construction : 응력값은 구조물이나 기계요소의 강도와 안정성을 평가하는데 사용된다. 응력값을 분석하여 부재의 최대 응력, 응력 분포 · 집중 등을 확인할 수 있다. 이를 통해 구조물의 강도를 검증하고 재료의 파괴 가능성이나 변형 가능성을 예측할 수 있다. 응력값 분석은 구조 설계, 재료 선택, 부품 제작 등 다양한 공학 응용에 활용된다.
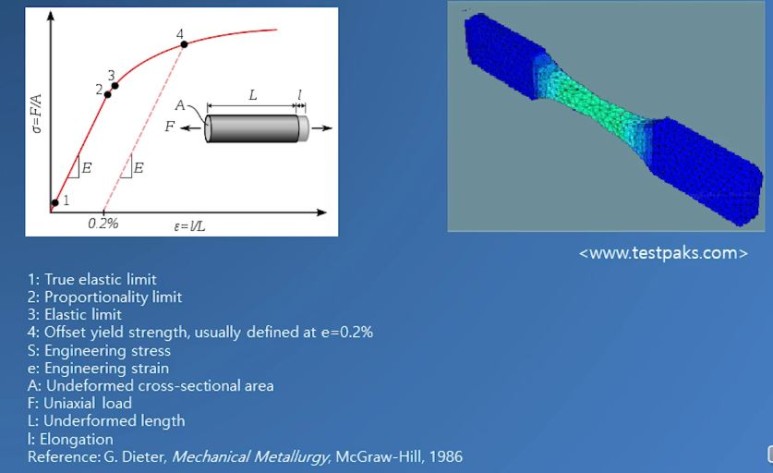
Manufacturing and Material Science : 응력값은 재료의 기계적 특성을 평가하는데 사용된다. 재료의 응력 변형 특성을 분석하여 인장강도, 굽힘 강도, 연신율 등을 평가할 수 있다. 이를 통해 적절한 재료 선택, 재료의 가공 공정 최적화, 구성요소의 재료 개선 등이 가능하다.
Geotechniacl Engineering : 응력 값은 지반의 응력 상태와 안정성을 평가하는데 사용된다. 지반에 가해지는 응력을 분석하여 지진, 토사의 소용돌이 등의 자연재해로 부터 지반의 반응을 예측하고 토설 및 지반 안정성 설계 등에 활용된다.
Biomechics and Biomedical Engineering : 응력값은 생체재료나 조직에서의 응력 분석에 사용된다. 예를 들어 인체 뼈나 조직에서 응력을 분석하여 부하에 대한 반응을 평가하고 인공장기 설계, 의학적 치료 기술 개발 등에 사용된다.
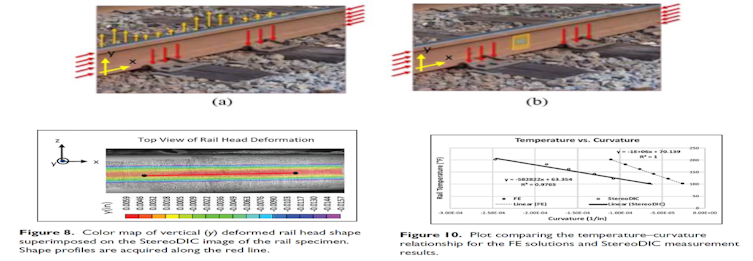
위 그림과 같이 열화상 촬영 등을 활용하여 온도에 따른 변위를 측정하여 Stress와 온도 사이의 관계를 분석하는 등, 응력을 측정하여 재료 분석에 활용할 수 있다.
#응력 #전단력 #압력 #연신률 #변형 #인장응력 #인장강도
'소방설비기사 (기계) > 기초물리' 카테고리의 다른 글
| 열역학 제1·2법칙 : 에너지보존법칙, 가역과정 · 비가역 과정 (0) | 2024.08.14 |
|---|---|
| 열역학 제1법칙 (등적 · 등압 · 등온 · 단열과정) (0) | 2024.08.13 |
| 응력 (Stress, σ)란 무엇인가 ? (0) | 2024.08.12 |
| 일반기체상수(R)와 특정기체상수(R')와의 관계 (0) | 2024.08.12 |
| 기체의 밀도와 몰질량 (이상기체 상태방정식) (0) | 2024.08.08 |