1. 이상기체와 몰 (mol)
▣ 일반 물리학의 열역학 파트에서 생각할 수 있는 상태함수는 온도(T), 압력(P), 부피(V) 등이 있다. 열역학은 대부분 기체
의 운동에 관한 사항을 다룬다. 기체의 성질은 퍼져 나가는 성질(부피), 밀폐된 곳에서 기체가 운동을 할 때 밀폐된 벽을
때리는 기체운동 (압력), 기체가 운동함으로써 생기는 에너지 (온도) 등을 특징으로 가지고 있다.
◈ 이상이체
◈ 단위 : mol (몰)
◈ 아보가드로 수 : 6.02 × 1023 : Avogadro's number
▣ 일반 물리학 수준에서는 실제 기체 보다는 '이상기체 (Ideal gas)'를 주로 다룬다. 이 이상기체를 이해하려면 먼저 몰수
(mol)라는 개념을 알아야 하는데 1mol은 기체분자가 아보가드로수 6.02 × 1023 개 있는 양을 말하며, 구체적으로 탄소
(원자번호 12) 12g 에 들어있는 원자의 개수를 말한다.
▣ 만약 어떤 기체 속에 분자가 6.02 × 1023개 있으면 이 기체는 1[mol]의 양이 있다고 말한다. 그러므로 몰수는 다음과
같이 나타낼 수 있다.
⊙ 원자의 개수가 N개 일 경우

만약 기체속에 분자개수가 N개일 경우 어떻게 몰수로 환산하는지 알아보자.
1몰 [mol]은 어떤 기체속에 아보가드로수 (약 6.02 × 1023)개가 있는 경우를 말하므로 기체속에 들어 있는 원자의 수를
아보가드로 수로 나누어 주면 그 기체의 몰수(mol)를 계산할 수 있다.
2. 몰질량 M
1몰 (mol)에 해당하는 질량 M = mNA (m : 원소의 질량)
시료의 질량이 Wsample 이라고 하면

여기서 새로운 단위 mol과 함께 나오는 개념이 바로 몰질량이다. 몰질량은 '1mol에 해당하는 질량'을 말하며 영어 대문자 M으로 표현한다. 이때 몰질량 M은 m(원자량) × N (아보가드로수)로 구할 수 있다.
이 때 몰질량을 이용해 어떤 시료의 질량을 알고 있다면 그 시료의 몰수도 알 수 있다.
즉, 시료의 질량 (W)을 몰질량(M)으로 나누어 주면 된다.
3. 이상기체 (Ideal gas)란 ?

이상기체는 무엇일까?
위 그림과 같이 같은 온도에서 크기가 같은 용기에 각기 다른 기체 1mol을 각 용기에 담아 두었다고 하자. 이 때 기체의
밀도는 기체의 질량을 부피로 나눈 값이 된다. 1몰은 각각의 기체의 원소수가 아보가드로수 (6.02 × 1023) 만큼 들어 있는
양을 의미하므로 기체원소의 활동으로 인한 압력은 기체가 각기 다름에도 불구하고 유사하게 된다. 이와 같은 현상을
나타낸는 기체를 '이상기체 (Ideal gas)라고 한다.
가. 보일의 법칙
온도가 일정한 조건에서 기체의 부피 (V)가 압력(P)에 반비례한다. 즉, 기체의 부피와 압력을 곱한 값은 동일한 기체에 대하여 다음과 같이 상수값을 갖는다.
P V = constant
나. 샤를의 법칙
압력이 일정할 때 기체의 부피는 온도에 따라 선형으로 증가한다. 즉, 기체는 온도가 1℃ 오를 때 0℃ 부피에 비해여
1/273.15 만큼 비례하여 증가한다. 만약 온도를 -273.15 ℃ 로 내린다면 그 기체의 부피는 "0"이 된다고 샤를은 예측했다.
따라서 샤를의 법칙에 따르면 일정 압력하에서 부피(V)를 절대온도 (T)로 나눈값은 일정하게 된다.

다. 게이뤼삭의 법칙
부피가 일정할 때 압력은 온도에 비례한다.
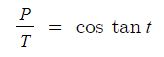
이와같이 기체의 압력, 부피 그리고 온도가 만족하는 관계는 온도가 극히 낮지 않고 또한 기체의 밀도가 희박한 경우에는
기체의 종류에 관계없이 잘 성립한다. 이와같이 위의 법칙을 잘 따르는 기체를 '이상기체'라고 한다. 이상기체는 분자의
크기가 거의 "0"이어서 용기속의 공간을 점유하지 않고 또한 분자끼리의 상호작용이 미치는 거리도 분자들 사이의 평균
거리보다 휠씬 적어서 거의 언제나 독립적으로 자유롭게 움직일 수 있는 가공의 기체이다.
앞에서 언급한 기체의 온도, 부피, 압력의 관계를 묶어서 보면 다음과 같다.

이렇게 기체의 압력(P)과 부피(V), 그리고 온도(T)가 가지고 있는 관계를 보일-샤를의 법칙이라고 한다. 만약 동일한 압력,
부피, 온도를 갖는 두 기체를 하나로 합하게 되면 부피는 2배가 되고 온도와 압력은 변함이 없을 것이다.

따라서 위 식처럼 constant로 표시된 일정한 값은 원래 값의 2배가 될 것이다. 즉, 이 값은 바로 기체에 포함된 분자의 양,
즉, 분자의 몰 수 n에 비례한다는 것을 알 수 있다. 상수(constant)값을 R로 놓으면 다음 같은 식이 된다.

또한 비례상수 R을 기체 상수라고 하고 이는 실험에 의해 정해진 양으로 다음과 같다.

이상기체의 법칙은 열역할적인 여러값들 사이의 관계를 보여주는 하나의 예로서 이것을 보다 일반적으로 이상기체 상태방
정식이라고 한다. 즉, 열역학적 변수들은 독립적이지 않고 서로 관련이 되어 있다는 것을 보여준다.
라. 아보가드로의 법칙 (Avogadro's law)
온도와 압력이 일정할 때 같은 부피에 들어 있는 분자의 수는 그 기체의 종류에 관계없이 일정하다는 것으로 이 법칙을
이용하면 이상기체의 법칙을 부편적인 것으로 이해할 수 있다.
즉, 분자 1[mol]에 들어 있는 분자의 수인 아보가드로수 (Avogadro's number) NA = 6.022 137 × 1023 ≒ 279 를 이용하면
이상기체 상태방정식은 다음과 같이 표현할 수 있다.
P · V = N k T
여기서, k = R / NA
k를 볼츠만의 상수라고 하며 다음과 같다.
k = (1.380 658 ± 0.000043 ) × 1023 [J/K]
【 또다른 이상기체 상태방정식】
가. 보일의 법칙
▣ 온도가 일정할 때 기체의 부피는 그 기체의 압력에 반비례한다.

나. 샤를의 법칙
▣ 압력이 일정할 때 기체의 부피는 절대온도에 비례한다.

다. 아보가드로 법칙
▣ 기체의 부피는 그 기체의 몰수 (mol)에 비례한다.

위의 식을 종합하면 다음과 같이 나타낼 수 있다.

위 식에서 양변에 압력 (P)를 곱하고 비례기호를 등호로 바꾸고 비례상수 K를 붙이면 다음 식이 성립된다.
P · V = n · k · T
위 식에서 비례상수 k는 아주 유명한 상수이다. 그래서 특별히 R이라는 이니셜을 부여해서 기체 상수라고 부른다.
P · V = n · R · T
여기서 P : 압력, V : 부피, n : 분자수(몰수), R : 기체상수, T : 절대온도
위 식을 이상기체 상태방정식이라고 한다.
위 식에서 기체 상수 R을 구해보자. R = PV / nT 가 된다. 기체상수 R을 구하기 위해서는 압력(P), 부피(V), 몰수(n), 온도(T)
를 알아야 한다. 표준상태(S.T.P)를 가정하여 P, V, n, T 값을 적용해 보자
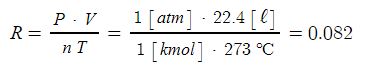
4. 공기의 밀도
▣ 공기의 밀도는 압력 (P)가 높아지면 커진다.
▣ 공기의 밀도는 온도가 높아지면 작아진다.

여기서, ρ : 공기의 밀도
P : 공기의 압력
R : 공기의 기체상수
T : 공기의 절대온도
#이상기체 #이상기체상태방정식 #보일 #샤를 #보일샤를의법칙 #아보가드로 #Avogadro #압력 #밀도 #부피 #기체상수 #상태방정식 #아보가드로수
'소방설비기사 기계실기 이론' 카테고리의 다른 글
| 연결살수설비 소방설비기사 기계분야 실기 이론 (0) | 2023.12.14 |
|---|---|
| 연결송수관설비 - 소방설비기사 기계분야 실기 이론 (0) | 2023.12.13 |
| 제연설비 - 누설틈새면적 산정법 (2) | 2023.12.01 |
| 소화활동설비 - 제연설비 2 (2) | 2023.12.01 |
| 소화활동설비 - 제연설비 1 (4) | 2023.11.29 |
