아낌없이 주는 나무

1. 유체(Fluid) 란 ?

유체란 어떤 물질에 전단력을 가해 변형이 이루어지는 과정에 전단력을 회수하더라도 일정

시간 동안 변형을 계속하는 물질을 말하며 이 때 변형은 아무리 작은 전단력이 가해져도

이에 저항하지 못하고 변형된다고 가정을 한다.

​

2. 점성 (Vicosity)이란 ?

일반적으로 점성이란 끈적임을 말한다. 유체에 있어서 점성이란 전단력이 가해졌을 때 그 힘에 저항하여

그 물체가 원래 상태를 유지하려고 하는 성질을 말한다. 여기서 전단력은

어떤 물질의 면에 접선방향으로 서로 엇갈기게 작용하는 힘을 말하며 이러한 힘에 저항하려

는 유체의 고유 성질을 점성이라고 한다.

​

3. 액체와 기체의 점성

액체의 점성은 물의 입자간에 서로 잡아 당기는 힘에 의하여 발생한다.

물의 예를 들면 물은 H2O로 산소원자 하나에 수소원자 2개가 결합하여 분자를 구성하는데 수소원자 2개가 서로

편향되어 결합되어 자석처럼 서로 입자간에 당기는 힘이 작용하여

이로 인해 점성이 발생한다. 그런데 액체의 온도가 올라가면 전자들의 움직임이 활발해져

응집력이 약해져서 점성이 작아 지는 경향을 보인다.

반면 기체의 점성은 기체입자간의 충돌 즉, 마찰에 의하여 발생하는데 온도가 올라가면 입

자들의 운동이 활발해져 마찰이 증가하여 점성도 커지게 된다.

​

4.. 뉴턴의 점성법칙 (Newtonian 유체)

어떤 물체에 전단력을 가했을 때 가해진 시간에 관계없이 전단력에 의한 물체의 변형이 일정하게

이루어져는 유체를 Newtonian 유체라고 부른다.

위 그림의 노란 정4각형 모양의 유체입자가 있다고 가정하자. 아래면은 고정되어 있고 최상

층 입자는 전단력이 화살표 방향으로 온전히 전해져 평형사변형으로 변형되었다고 하자.

이때 유체의 변형률을 당초 사각형 한변의 길이 대비 변형된 길이라고 하고 변형률을 ε이라

한다. 변형률을 수식으로 나타내면 변형률 ε = dx / dy 가 된다. 정사각형이기 때문에 x =y

는 같다. 가로와 세로의 길이가 같기 때문이다.

이제 변형률 ε을 미분을 하면 다음과 같은 식이 성립된다.​

위식에서 dx/dt는 길이를 시간으로 미분하였으므로 속도 (v,u)가 되고 위와 같이 변형률을

미분하였더니 변형률이 y값 즉 (높이, 두께)에 대한 속도와의 관계로 관계식이 변하게 된다.

그런데 Newtonian 유체는 변형률의 변화율 (속도)과 전단력과 선형관계(비례관계)에 있

다고 했으므로 다음과 같은 식이 성립된다.​​

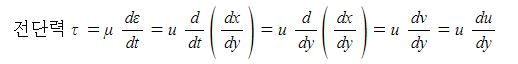
위 식에서 μ를 점성계수라고 하고 단위로 [Pa · sec]을 쓴다. 점성계수는 전단력과 y(높이,

두께)에 대한 변형률의 변화율 (속도)와의 관계를 나타내는 상수라고 할 수 있다.

​

이를 좀 더 상세하게 알아 보기 위해 아래 그래프와 같이 유체로 채워진 정4사각 평면위의

작은 미소면적을 가정하고 x축에서 y축 방향으로 일정 거리 만큼 떨어진 곳 까지 유체가

채워져 있고 유체의 최상층에서 x축과 평행한 방향으로 전단력을 가해 막대를 움직인다고

가정해 보자.

이 막대와 주변을 채운 유체 사이에는 점성력이 작용하여 막대를 u의 속도로 끌어 당기면

막대와 x축 사이에 있는 유체는 평행사변형 모양으로 변형 (변형각 dθ)가 일어난다.

이 때 막대의 접선방향 움직임에 대한 전단응력 (Shear stress)을 τ 라고 놓으면 이 힘의 크

기는 각속도 변형률 dθ / dt 에 비례한다.​

또한 그림으로 부터 다음이 성립하며 무한이 작은 변화를 가정하면 각속도 변형율 (dθ / dt)은 y축 방향으로의

속도 (u, x방향)의 경사와 같다고 놓을 수 있다.

위 두식을 조합하면 전단응력 (Shear stress)와 비례하며, 이 둘 사이의 비례상수 μ를 도입

하면 아래와 같이 나타낼 수 있다. 이 때 비례상수 μ를 점성계수라고 하고 [FT/L2],[M/LT)

의 단위를 가진다.​

이 식을 다시 살펴보면 점성계수(μ)가 크면 클 수록 어떤 동일한 전단응력(τ)에 대하여 속도경사 (du/dy)가

작아져야 하고 (즉, 변형률이 작고) 점성계수가 작으면 변형률이 커져야 한다는 것을 의미한다.

​

5. 동점성계수 (Kinematic Viscosity)

​

점성계수를 유체의 밀도로 나눈 형태로 사용하기도 하는데 이를 동점성계수 (v)라고 한다.​

6. 뉴턴 유체와 비뉴턴 유체 (Newtonian vs Non-Newtonian Fluid)

뉴턴의 점성법칙에서 점성계수 (μ)가 상수이면, 전단응력과 각속도 변형률은 선형관계가

되며 이러한 유체를 뉴턴 유체라고 한다. 다시말해 위에서 말한 유체가 점성유체이다.

​

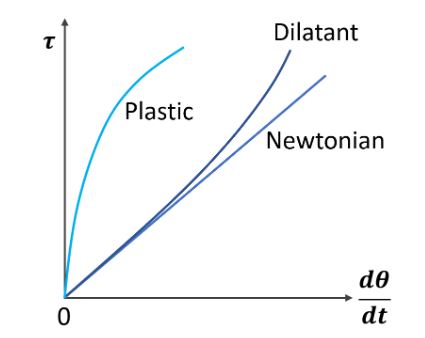
비뉴턴 유체는 전단응력과 각속도 변형률의 관계가 비선으로서 점성계수 (μ)를 상수로 표현

할 수 없는 경우이다. 이 말은 힘이 해당 유체가 힘이 작게 작용할 때는 매우 큰 점성을 보이

다가 전단응력이 강해질수록 유체의 각속도 변화율이 작아지거나 (Dilatant), 반대로 전단

응력이 강해질수록 각속도 변형률의 변화율이 커지는 경우(Plastic)를 말한다.

7. 레이놀즈 수 (Reynolds number)와 점성의 관계

층류와 난류의 특성을 기술하기 위한 무차원 수인 레이놀즈 수 (Raynolds number)는 아

래 식과 같이 점성계수 (μ)를 포함하고 있다.​

(여기설 ρ : 유체의 밀도, V는 유속, L은 흐름의 길이다.)

다시말해 점성의 강도에 따라 유체가 층류가 되거나 난류가 될 수 있다. 레이놀즈 수는 관성

력과 점성력의 비율로 정의된다. 점성계수가 주어진 상황이라면 관성력의 크기에 따라 난류

와 층류 흐름이 바뀔 것이고 같은 흐름 상태라면 점성계수가 이를 결정한다고 볼 수 있다.

​

일반적으로 Re가 약 2,100 이하이면 층류(laminar flow), 4,000이상이면 난류(turbulent flow), 2,900 ~ 4,000 사이를

천이 영역(transition region)으로 구분하기도 하는데, 사실 정확한 숫자로 딱 잘라 구분할 수 있는 것은 아니다.

​

#점성 #점성계수 #뉴톤 #레이놀즈 #뉴턴유체 #점성유제 #전단력 #전단응력 #선형곡선

#동점성계수 #유체 #응집력 #탄성계수 #평행사변형 #속도 #변형률 #접선

가. 고체 (Solid)

  ▣ 탄성체 (Elastic Solid)

  ▣ 소성체 (Plastic Solid)

   ※ 고체의 특성은 형태가 유지되고 결합력이 높아서 분자들이 움직이지 않고 밀도가 높다.

       분자간의 거리가 가깝고 압축성에 대한 강도가 매우 높다.

위 그림에서 X축 Strain은 변형율을 나타내고 Stress는 응력을 나타낸다. 응력과 변형률의

관계를 통하여 탄성체와 소성체를 구분하여 보자.

여기서 Stress는 단위 면적당 작용하는 힘이다. 즉 수직으로 작용하면 수직응력, 수평으로

작용하면 전단응력이라고 한다. Strain은 변형률이라고 했다. 변형률은 원래 길이 대비

변형된 길이이다.

위 그림에서 고체에 Stress를 가할 때 작용하는 힘과 변형률이 처음에는 선형적(비례관계)

에 있다가 어느 지점을 지나면 곡선의 관계로 변한다. 선형 관계가 끝나는 지점을 Yield

(항복점)이라고 부른다. 항복점까지 과정에서 가해지는 힘을 항복응력이라고 한다.

그리고 더 힘을 가해서 고체가 파괴되는 점을 Failure(파괴점)이라고 하고 이 때 가해지는

힘을 Failure Stress라고 한다.

Stress와 변형률과의 관계가 선형적인 관계를 갖는 것을 탄성체라고 부른다. 탄성체의

특성은 파괴되지 않는 한 힘을 가했다가 중단하면 원래의 형태로 복귀한다. 그런데 항복점

을 넘어서면 가했던 힘을 회수해도 원래 모양대로 복귀하지 않는다. 이런 성질을 소성체라

고 한다.

위 그림에서 선형관계를 유지하는 동안의 Stress와 Strain의 비율을 Young's Modulus,

탄성계수, 강성계수 등으로 부른다. 이 때 이 계수의 단위는 응력의 단위와 같다. 그 이유는

Strain은 당초 길이 대비 변형된 길이 이므로 단위가 없다. Stress는 응력의 단위이므로

Stress를 Strain으로 나누면 그 단위는 Stress 즉 응력의 단위가 된다.

​

[Stress - Strain curve showing typical yield behavoir for nonferrous alloy's]

고체 물질은 그 물질을 이루는 구성성분에 따라서 다른 성질을 갖는다.

위 그림은 Nonferrous alloys로 비철합금을 예로 든 것이다. 합금금속 고체의 경우에는

위 그림의 그래프에서 x축은 L은 원래의 길이, l은 변형된 길이를 나타내고 Y축은 응력

즉 힘/단위면적을 나타낸다. 그래프에서 1~2.단계는 탄성거동을 하는 구간이고 점 2를

지나면 비탄성 거동을 하게 된다. 오른쪽 그림은 어떤 물체에 인장력을 가했을 때 변형이

일어나는 것을 보여주고 있다. 처음에는 양쪽에서 잡아 당기면 빨간색으로 변하는데 이는

응력이 작용한 결과이다. 늘어나면서 어떤 일이 일어나느냐 하면 고체는 부피가 변하지

않으려고 하는 성질 때문에 늘어나면서 동일 부피를 유지하기 위해 가늘어지게 된다.

​

[A stress - strain curve typical of structual steel (ductile)]

위 그림은 ductile 소재를 예로 든 것인데 ductile 이란 늘어나는 연상소재를 말한다.

위 그림에서 실제 응력탄도는 파란색 그래프처럼 움직인다.

그런데 빨간색은 이론적인 탄도를 나타낸 것이다.

그런데 실제와 이론적인 거동이 비슷한 것은 탄성거동 과정으로 서로 비슷하게 움직인다.

A는 겉보기 응력을 나타내고 B는 실제 응력 거동을 나타낸 것이다.

고체의 경우 취성 거동을 보이는 물질이 많은데 취성거동은 위 그래프와 같이

탄성거동이 나타나지 않고 파괴점이 금방 나타나는 물질을 말한다.

​

나. 유체 (Fluid)

  ▣ 액체 (Liquid)

  ▣ 기체 (Gas)

     [Phase Diagram]

위 그림은 물의 온도와 상의 변화를 나타낸 것이다.

​

[Properties of water]

물의 대표적인 특성은 위 그림의 왼쪽 아래와 같다.

즉, 높은 비열, 중성물질, 높은 열전동성, 3상 물질, 높은 용해성, 고체 부피가 액체 부피보

다 크다는 것 등이 물의 대표적 특성이다.

물은 지구상에서 가장 흔한 물질이다. 지구상의 물은 대부분 액체상태로 존재하고 다음으로

고체 즉 얼음 형태로 존재한다.

그림의 오른쪽을 보면 맨 위는 얼음(고체), 가운데는 액체, 아래는 수증기(기체)의 분자구조

를 나타낸다. 고체일 때 물분자가 강한 결합력을 가지는 것은 물분자가 한쪽은 양(+), 다른

쪽은 음(-)의 전기적 특성을 나타내기 때문이다.

이러한 분자적 특성이 나타나는 것은 표면장력에서 볼 수 있다.

오른쪽 아래 그림을 보면 왕관현상이라고 하는 물방울이 수면위로 튀어오르는 모습을

볼 수 있는데 물결 뿐만 아니라 솟아오르는 물기둥, 위에 완벽한 구 모양의 물방울까지 보이

는데 이와 같은 형태가 만들어지는 가장 큰 이유가 왼쪽 가운데 그림처럼 물분자의 극성 때

문이다. 물분자의 극성 때문에 만들어지는 것이 표면장력이다. 예를 들어 유리창에 물을

뿌리면 큰 덩어리는 중력 때문에 떨어지지만 대부분 얇은 막을 형성하여 증발할 때까지

유리창에 붙어 있는 것을 볼 수 있다. 이는 중력 보다 훨씬 큰 얇은 막의 표면장력을 형성

하기 때문에 유리창에 붙어 있게 된다.

물은 비열이 매우 크다. 비열은 어떤 물질이 가질 수 있는 에너지의 양을 말한다.

비열이 크다는 것은 에너지를 많이 저장할 수 있는 물질이라는 것이다. 물은 비열이 매우

크므로 에너지를 많이 저장할 수가 있다.

물은 산성도 아니고 알칼리성도 아닌 중성 물질이다.

물은 열 전도성이 높기 때문에 깊은 바다의 온도를 재 보면 상당한 깊이까지 물의 온도가

비슷함을 알 수 있다.

물은 똑 같은 H2O 분자구조를 가지고 있으면서도 고체, 액체, 기체 상태로 나타나는 3상

물질이다. 물은 용해도가 높아 다른 물질을 포용하는 양이 많은데 물이 용해도가 높은 것이

지구상에 생명이 살아 있는 이유가 된다. 식생이 살아가기 위해서는 많은 영양분이 필요한

데 땅속의 많은 영양성분 즉 미네날이 물에 녹아서 식물에 흡수할 수 있도록 해 준다.

물은 지구상에서 유일하게 고체의 부피가 액체의 부피보다 큰 물질이다.

​

※ Real Fluid vs Viscous Fluid

  ▣ 이상 유체 (Ideal Fluid)

  ▣ 실제 (점성) 유체

    ⊙ Newtonian Fluid

    ⊙ (Non-Newtonian) Plastic Fluid

물체의 또 다른 성질인 점성에 대하여 알아보자.

점성은 끈적임인데 끈적임의 강도는 고체에는 없고 액체에 많다. 모든 유체는 점성이 있다.

땅콩 버터와 실리콘이 유체일까 ? 유체로 구분된다.

땅콩 버터는 물의 끈적임을 1로 보았을 때 꿀은 10만배인데 꿀보다도 100배가 많은 끈적

임의 강도를 갖고 있다. 실리콘은 물의 10^10 배의 끈적임을 갖고 있다.

​

  ▣ 압축성

  ▣ 비압축성

유체의 성질중에 압축성과 비압축성이란 성질이 있다.

물도 압축성이 크지는 않지만 있다.

위 그림의 위쪽을 보면 잠겨진 밸브가 있는데 밸브를 열면 물이 흘러간다. 이 때 다시

밸브를 잠그게 되면 물이 왼쪽에서 오른쪽으로 흘러가는데 밸브를 잠그면 물의 흐름

에 의해 망치로 밸브를 때리 듯 아주 큰 충격이 발생하게 된다. 이를 수격작용이라고

한다. 기체의 압축성은 비행기의 소닉붐(Sonic Bomb)현상으로 설명할 수 있다.

초음속기가 음속을 돌파하면 비행기 바로 뒤쪽에서 꽃깔 모양의 구름이 형성되는데

이를 소닉붐이라고 한다. 이는 공기의 압축성에 의해 발생하게 된다.

​

▣ 유체란 ?

  ⊙ 전단응력이 작용한 후 제거하여도 연속적으로 변형을 하는 물체를 말한다.

고체는 위 그림처럼 분자간의 결합력이 매우 강한 물질이다. 고체는 매우 강한

분자간의 결합력에 의해 주어진 전단력을 제거하게 되면 바로 현상력이 작용

하여 복귀가 되거나 그 상태를 유지하게 되나

유체는 분자간의 결합력이 약해 전단력이 가해지면 위쪽의 분자들 부터 쓸려

나가며 연속하여 변형이 이루어지다가 전단력이 제거되어도 당분간 변형이

계속되는 물질을 말한다.

즉, 고체와 유체를 구분하는 기준은 전단력이 가한 후 이를 제거하였을 때 변형을

계속하는 지 여부에 따라 구분을 하게 된다.

​

#유체 #이상유체 #실제유체 #전단력 #열전도성 #현상력 #용해도 #중성 #산성

#알칼리성 #압축성 #점성 #탄성체 #소성체 #탄성거동 #비례관계 #항복점

#파괴점 #원자 #분자 #원자핵 #전자

​