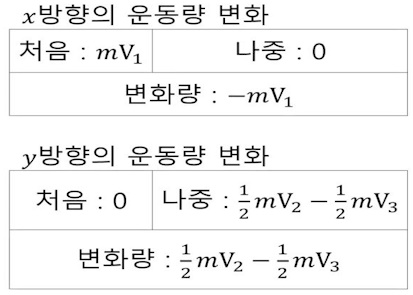
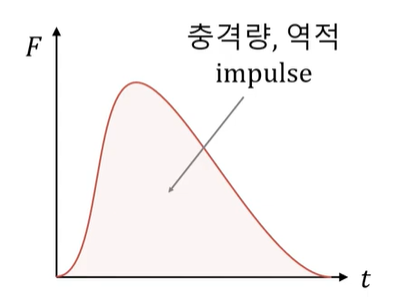
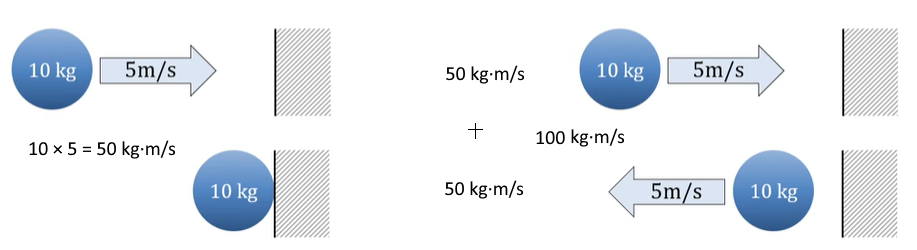
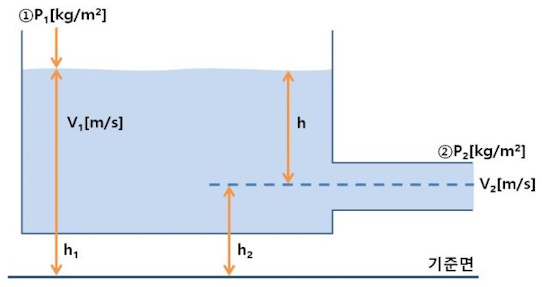
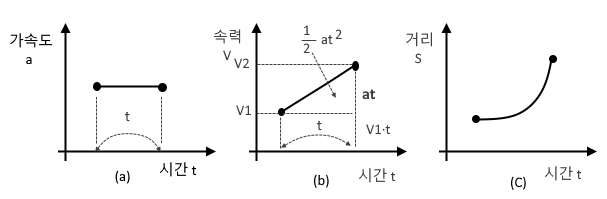
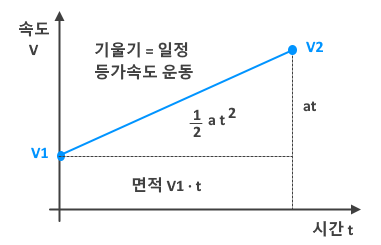
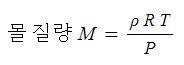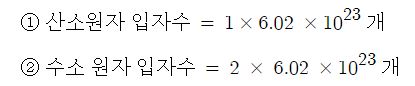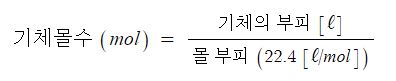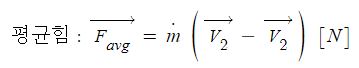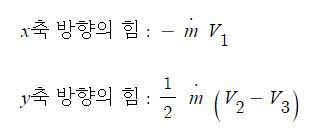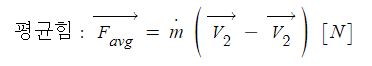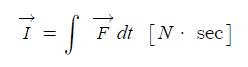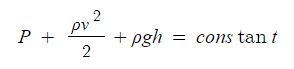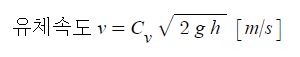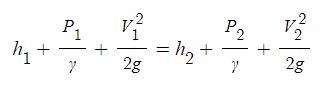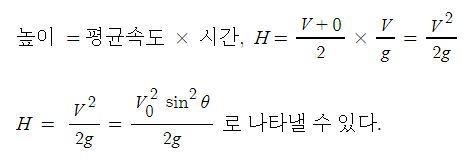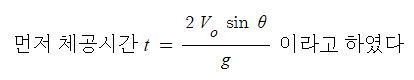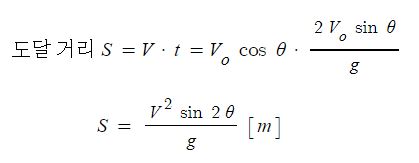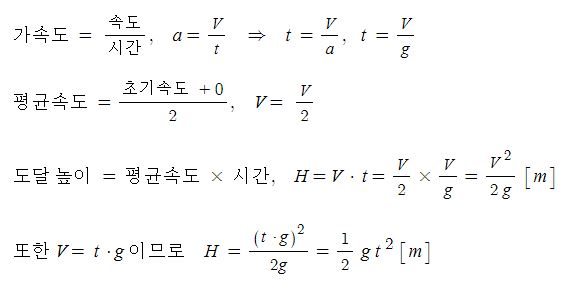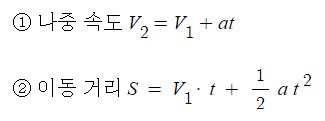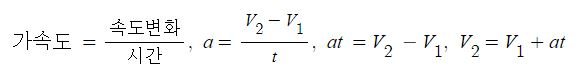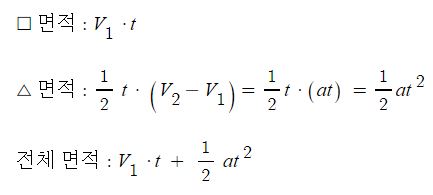일반 기체 상수 : P V = n R T , 특정 기체 상수 : P V = m R T
이상기체 상태방정식에 적용하는 기체상수에는 일반기체 상수 (R)와 특정기체상수(R')가 있다. 이 기체 상수는 모두 기호로 R을 똑 같이 사용하기 때문에 혼동하는 경우가 많다.
이들 기체 상수가 어떻게 구분되는지 알아 보자.
기체의 상태를 분석하는데 사용하는 기본 공식으로 이상기체 상태방정식이 있는데 여기에 사용하는 기체상수로 일반기체상수가 적용되느냐, 특정기체상수가 적용되느냐에 따라 이상기체 상태방정식이 다음과 같이 구분된다.
|
구 분
|
일반기체상수(R)
|
특정기체상수 (R')
|
|
이상기체 상태 방정식
|
P V = n R T
|
P V = m R T
|
|
배열과의 관계
|
-
|
R = Cp - Cv
|
1. 일반 기체 상수
가. 보일의 법칙
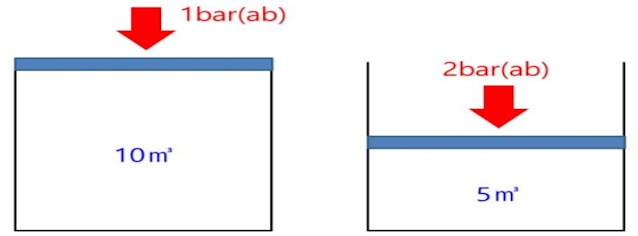
보일의 법칙에 따르면 온도가 일정하다면 표준상태 (0℃, 1기압)에서 기체의 부피는 압력에 반비례한다고 한다.
P1 · V1 = P2 · V2
나. 샤를의 법칙
샤를의 법칙에 따르면 압력이 일정하다면 표준상태에서 기체의 부피는 절대 온도와 비례한다고 한다.
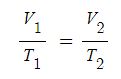

그런데 보일의 법칙과 샤를의 법칙은 합하여 하나의 식으로 나타낼 수 있다.
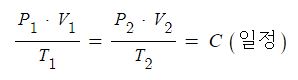
다. 아보가드로의 법칙
아보가드로는 표준상태 (0℃, 1기압)에서 기체 상태의 물질은 원자량, 분자량 만큼의 질량(g)을 가진 기체의 부피를 1몰 (mol)이라 하는데 모든 기체는 표준상태에서 원자량, 분자량은 달라도 그 부피는 22.4 ℓ 로 동일하고 입자수도 6.02 × 10^23 개로 같다는 것을 알아 냈다.
따라서 아보가드로의 법칙에 따르면 표준상태에서 기체의 부피는 그 기체의 몰수에 의해 결정된다고 한다. 이를 식으로 나타내면 다음과 같다.
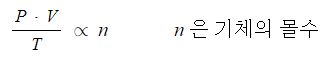
그런데 위 비례식을 등식으로 만들기 위해서 사용하는 비례상수가 일반기체상수 (R)이다.
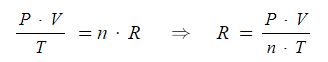
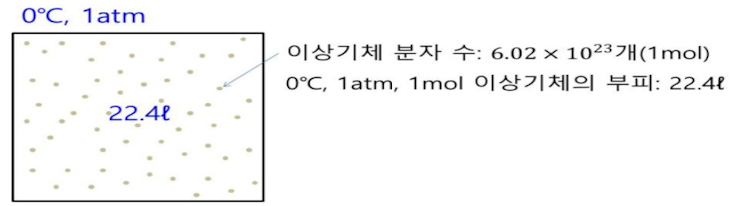
표준 상태에서 1기압 (101,325 [Pa] = 101,325 [N/㎡]), 0 [℃] (273.15 K)인 이상 기체 1 몰(mol)의 부피는 22.41 [ℓ] 이다. 이를 위 식에 대입하여 일반기체상수 (R)을 계산해 보면 8.314 [J/mol · K]이라는 값을 얻을 수 있다.
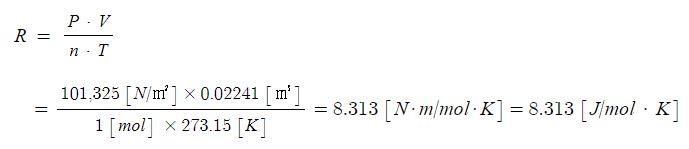
기체상수는 기체가 이상기체라고 가정한다면 기체의 종류와 관계없이 일정한 값이 된다.
일반기체상수를 이용하여 이상기체상태방정식을 다음과 같이 표현한다.
P V = n R T
2. 특정 기체 상수
일반기체상수는 모든 기체에 동일하게 적용되는 비례상수이다. 아보가드로 법칙에 의하면 모든 기체는 표준상태에서 1 몰 (mol)의 부피가 같기 때문에 1 몰 (mol)을 기준으로 모든 기체에 적용할 수 있는 비례상수를 도출하게 되는데 이를 일반기체상수라고 부른다.
반면, 특정 기체 상수는 특정한 기체, 개별 기체의 상태방정식에 적용하는 비례상수를 말한다. 개별 기체에 적용하기 위해 일반 기체 상수를 해당 기체의 몰 질량으로 특정기체상수를 산정한다. 즉, 일반기체 상수는 모든 기체에 적용하기 위해 기체 1몰 (mol)을 기준으로 비례상수를 정하는 반면, 특정 기체 상수는 해당 기체에 적용하기 위해 일반 기체 상수를 해당 기체의 몰질량으로 나누어 해당 기체 1 [g]을 기준으로 비례상수를 산정한다.
예를 들면, '수증기'의 분자식은 H2O이다. 분자량은 18이고 몰질량은 약 18 [g/mol] 이다. (수증기 1몰 (mol)의 무게가 18[g]이라는 뜻이다)
이를 이용하여 일반기체상수 8.314 [J/mol ·K]의 몰 단위 일반기체상수를 몰질량 18 [g/mol] 으로 나누어 주면 수증기의 특정기체상수 0.462 [J/g · K]를 얻을 수 있다.
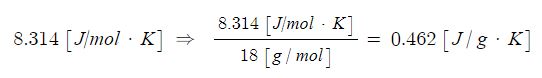
같은 방법으로 '공기 (몰질량 : 약 29 [g/mol]), 암모니아 (약 17[g/mol]), R-22 (약 86.5 [g/mol]) 등을 이용하여 해당 기체의 특정 기체상수를 구할 수 있다.
위에서 말한 기체의 몰질량과 특정기체상수는 다음과 같다.
|
구 분
|
암모니아
|
수증기
|
공기
|
R-22
|
|
몰질량 [g/mol]
|
17
|
18
|
29
|
86.5
|
|
특정기체상수 [J/g·K]
|
0.188
|
0.462
|
0.287
|
0.096
|
일반기체 상수를 Rideal, 특정 기체상수를 Rspecific 라고 하면 이상기체 상태방정식은 다음과 같이 나타낼 수 있다.
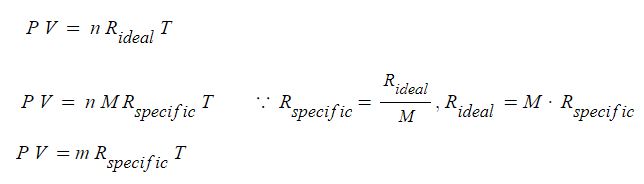
여기서, M : 몰(mol) 질량, m : 기체의 질량
특정기체상수를 이용한 이상기체상태방정식도 일반적으로 PV = mRT 등으로 나타내는데,
이 때 기체상수 R은 특정기체상수임을 주의해야 한다.
3. 비열과의 관계
어떤 기체가 열을 받으면 이 기체는 온도가 상승함과 동시에 부피가 증가하게 되는데
이 때 '온도 상승'과 '부피의 팽창' 비율은 특정 기체 상수에 따라 정해진다.
어떤 기체가 동일한 '정적 비열'을 가진다고 가정한다면 '특정 기체 상수'가 높으면 이 기체가 열을 받았을 때 외부로 더 많은 일을 하게 된다(온도 변화 대비)고 한다.
특정 기체 상수는 기체의 몰질량이 작을 수록 (다시 말하면 기체가 가벼울 수록) 커지므로
'열을 받은 기체의 몰질량'이 작을 수록 외부로 더 많은 일을 한다(단, 비교하는 기체들이 동일한 정적 비열을 가진다는 가정에서)는 의미가 된다.
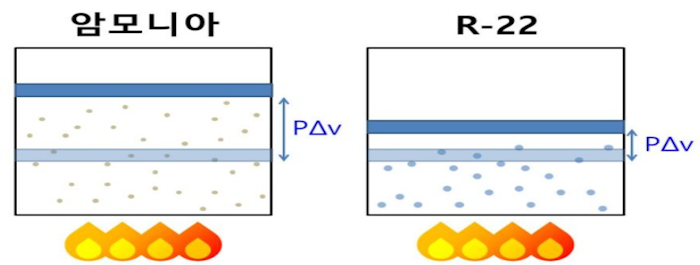

여기서, P · △V : 열을 받은 기체가 외부에 한 일
R' : 특정기체 상수, M : 기체의 몰질량
#기체상수 #일반기체상수 #특정기체상수 #몰질량 #이상기체 #상태방정식 #비열 #온도
'소방설비기사 (기계) > 기초물리' 카테고리의 다른 글
| 응력 (Stress, σ), 응력의 측정 및 사용목적 (1) | 2024.08.12 |
|---|---|
| 응력 (Stress, σ)란 무엇인가 ? (0) | 2024.08.12 |
| 기체의 밀도와 몰질량 (이상기체 상태방정식) (0) | 2024.08.08 |
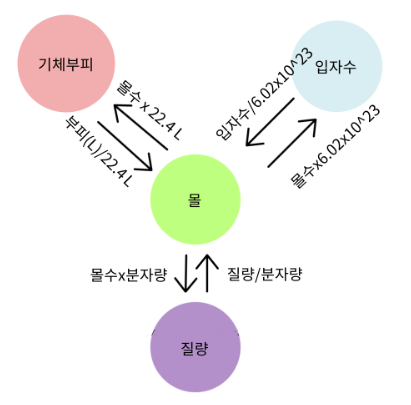
| 몰(mol), 몰질량, 몰부피, 입자수 사이의 관계 (0) | 2024.08.08 |
| 분류에 의해 작용하는 힘 (0) | 2024.08.07 |