'전기인이 되는 길 > 전자기학' 카테고리의 다른 글
| 가우스 정리, 포아송 방정식, 라플라스 방정식, 공식정리 (2) | 2021.11.14 |
|---|---|
| 벡터의 적분, 발산 정리 - 전자기학 (0) | 2021.11.12 |
| 전속과 전속밀도 (0) | 2021.11.11 |
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
| 가우스 정리, 포아송 방정식, 라플라스 방정식, 공식정리 (2) | 2021.11.14 |
|---|---|
| 벡터의 적분, 발산 정리 - 전자기학 (0) | 2021.11.12 |
| 전속과 전속밀도 (0) | 2021.11.11 |
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
▣ 대칭 전하 분포에 의한 전계의 세기를 구할 때 사용한다.
가우스의 법칙하면 전계의 세기와 연관하면 된다.
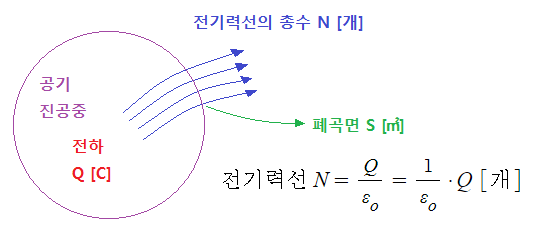
▣ 정의 : 임의의 폐곡면(S)을 통해 나오는 전기력선의 총수는 그 폐곡면 안에 있는
전하 (Q)의 1/εo 배와 같다.
※ 가우스의 법칙은 어느 공간에 구형태의 공간을 가정한 다음에 그 공간 구의 체적에서
발산하는 자기력선과 구의 표면에서 나오는 자기력선은 같다는 정리로 부터 자기력선의
밀도 즉 전계의 세기를 구하는데 사용된다.
구의 체적에서 전기력선의 발산을 구한다든지, 구의 표면에서 면의 단위면적당 전기력선의
밀도를 구한 다음 이를 적분하여 전계의 세기를 구하게 된다.
※ 구의 체적에서 전기력선의 발산을 구한다든지 구 표면의 전기력선을 밀도를 통해 전계의 세기를
구할 때 면적분과 체적적분을 사용하기 때문에 이를 이를 가우스법칙의 적분형이라 한다.
※ 또한 전계의 세기는 거리의 제곱에 반비례하고 어느 공간상에서 Q[C]이 있을 때 이로 부터
r[m] 떨어진 곳의 +1[C]이 받는 힘인 전계의 세기는 Q[C]를 거리의 제곱으로 나누어 주게 되고
유전율이란 1[m]에 1[V]의 전위차를 발생시키기 위한 전하량이라고 정의할 수 있으므로
전계의 세기는 다시 유전율로 나눠주면 된다. 따라서 아래와 같이 전기력선의 밀도를 구할 수
있는데 이를 가우스 법칙의 미분형이라 부른다.
① 가우스 법칙의 적분형
▣ 전기력선의 총수
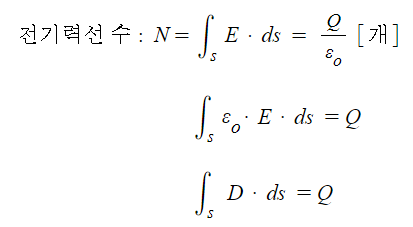
⊙ 특정 지점에서 구의 표면에서의 단위 면적당 전기력선의 밀도를 적분을 하게 되면 전체 전기력선의
총수를 구할 수 있다. 이 전기력선의 수는 전체 전하량을 유전율로 나눈 값과 같게 되는데
양변을 유전율로 나누어 주게 되면 유전율 × 전계의 세기란 좌변의 식을 구할 수 있다.
이는 전속밀도와 같게 되므로 구 표면의 전속밀도를 적분하게 되면 결국 총 전하량이 된다.
② 가우스 법칙의 미분형
▣ 전기력선의 총수 N


적분기호를 제거하게 되면 가우스의 미분형을 취할 수 있다.
① 가우스 법칙의 미분형
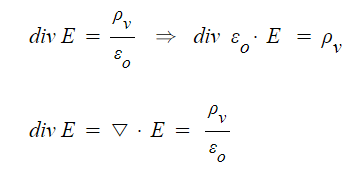
▣ 가우스법칙 미분형에서 전계의 발산은 특정 공간에서 체적전하 밀도를 유전율로 나눈 값과 같게되고
양변에 유전율을 곱해 주면 체적전하밀도는 전계의 발산에 유전율을 곱해주는 값이 된다.
② 전계의 세기 : E = - grad V = - ▽·V

※ 전계의 발산에서 전계 E는 - grad V로 바꿔 쓸 수 있고 이는 체적전하 밀도를 유전율로
나눈 값과 같게 된다. div는 ▽·로 바꿔 쓸 수 있고 grad 도 ▽로 쓸 수가 있다.
▽제곱은 라플라시안이라 부르기도 한다.
▣ 포아송 방정식의 용도

⊙ 체적전하밀도 (ρv)가 공간적으로 분포되어 있을 때 그 내부 임의의 점에서
전위(V)를 구하는 식이다.
⊙ 전위함수(V)가 주어지고 체적전하밀도 (ρv)를 계산할 때 사용한다.
※ ▽2 라플라시안이라고 함

※ 즉 (x, y, z) 축 방향에 대해 편미분을 2번 하라는 명령어다.
예제 1. 전위함수 V = x2 + y2 [V]를 형성하는 전위분포에서 1[㎥]안의 전하밀도
[C/㎥]를 구하면 ?
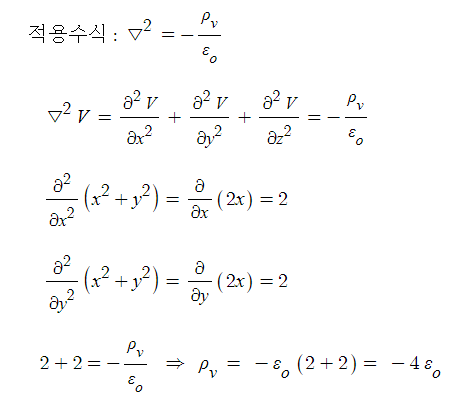
예제 2. 포아송의 방정식에서 전하가 분포되어 있지 않은 곳에서 라플라시안 ▽2=0이다.
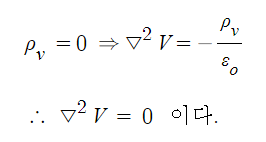
1. 전위 경도
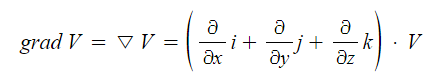
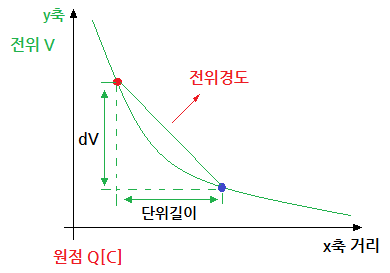
※ 전위경도는 전위의 기울기를 말하는 것으로 전위를 편미분하라는 의미이다.
편미분의 결과는 벡터로 표시되며 전위를 x, y, z 축에 대하여 편미분하면 된다.
2. 전계의 세기
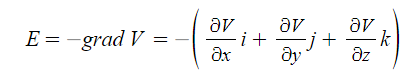
※ 전계의 세기는 전위 경도에 - 이다. 여기서 - 는 방향이 반대라는 의미이다.
전계의 세기는 전위와는 반대방향으로 나타난다는 의미이다.
즉 전계의 세기는 전위를 편미분하여 - 부호를 붙이면 된다.
3. 발산정리 (면적분 ↔ 체적적분)
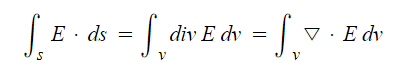
4. 전계의 세기와 전속 밀도 : D = εo · E
※ 전계의 세기에 유전율을 곱하게 되면 전속밀도가 된다. 전계의 세기는 결국 특정 지점에서
유전율로 나눈 값이 되므로 결국 전속밀도는 전계의 세기에 유전율을 곱한 값이 된다.
5. 가우스 법칙 : 전계의 세기를 산정하는 식
① 가우스법칙 적분형
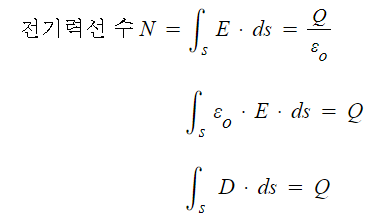
▣ 전기력선의 수는 구의 표면의 단위 면적당 전하밀도를 적분한 값이 되며
결국 전속밀도의 적분값이 총 전하의 값과 같게 된다.
② 가우스법칙 미분형
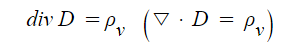
▣ 전속밀도 (전하량)의 발산은 체적 전하밀도와 같다. 체적전하 밀도를 전속밀도로
말을 바꾼 것과 같다.의미이다.
6. 포아송의 방정식
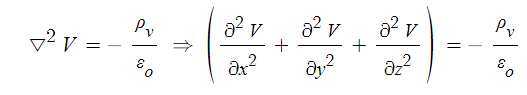
▣ 포아송의 방정식은 전위를 x, y, z 축에 대하여 2번 편미분하라는 의미이다.
7. 라플라스방정식
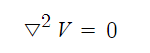
※ 어떤 공간내에서 전하량이 존재하지 않는 곳에서의 전위를 두번 편미분하게 되면
"0"이 된다는 의미있다.
| 전자기학 핵심요약 정리 - 전기기사 (0) | 2023.04.29 |
|---|---|
| 벡터의 적분, 발산 정리 - 전자기학 (0) | 2021.11.12 |
| 전속과 전속밀도 (0) | 2021.11.11 |
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
① 적분기호 : ∫ : sum의 S 기호화한 것이다. 즉 적분은 더하라는 의미를 기호화 한 것이다.
② 선적분 : 선의 길이를 구할 때 사용, 기호 : ∫l, ∫c, ∮, ∮c
③ 면적분 : 면적을 계산할 때 사용 : ∫s : S : square. 면적분의 S는 면적을 의미한다.
④ 체적적분 : 체적(부피)을 구할 때 사용 : ∫v : v : volume 체적적분의 v는 부피를 의미한다.
▣ 일정한 길이(선)나 넓이(면) 또는 부피(체적)에 존재하는 전하(Q)의 총량을 말한다.
※ 단위 길이, 넓이, 부피 당 전하량을 의미한다. 밀도를 구하는 것은 전체 중 일부분에 대한
단위당 밀도를 구해서 전체의 양을 구하기 위해 산정하게 된다.
① 기호 : ρl, = λ : 단위 길이당 전하량
▣ 선전하 밀도의 기호는 ρl, λ로 표시한다.


※ 적분식의 의미는 ① dl : 단위 길이에 대한 선전하밀도 ρl를 ② 전체 길이 L이 될 때까지 ③ ∫ : 더하라
라는 의미이다. 따라서 위의 식은 선전하밀도에 전체 길이를 곱한 값과 같게 된다.
① 기호 : ρs, : 단위 면적당 전하량


※ 적분식의 의미는 ① ds : 단위 면적에 대한 면전하밀도 ρs를 ② 전체 면적 s가 될 때까지 ③ ∫ : 더하라
라는 의미이다. 따라서 위의 식은 면전하밀도에 전체 면적을 곱한 값과 같게 된다.
① 기호 : ρv, : 단위 체적당 전하량


※ 적분식의 의미는 ① dv : 단위 체적에 대한 체적전하밀도 ρv를 ② 전체 체적 v가 될 때까지 ③ ∫ : 더하라
라는 의미이다. 따라서 위의 식 체적전하밀도에 전체 체적을 곱한 값과 같게 된다.
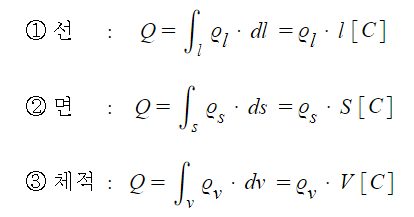
▣ 전기력선의 성질
⊙ 어느 점에서의 전기력선의 밀도는 그 점에서의 전계의 세기로 정의한다.
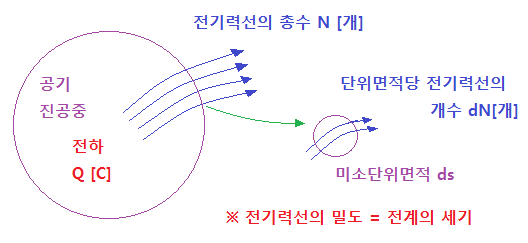
▣ 진공중에 전하 Q[C]의 전하가 있다고 할 때 이 전하로 부터 전기력선이 발산을 하게
된다. 이 전하에서는 N [개]의 전기력선이 발산하게 되고 특정 지점에서의 전기력선은
dN [개]가 된다. 특정 지점의 단위면적당 전기력선의 개수 즉 전기력선의 밀도가 그 점
에서의 전계의 세기가 된다.
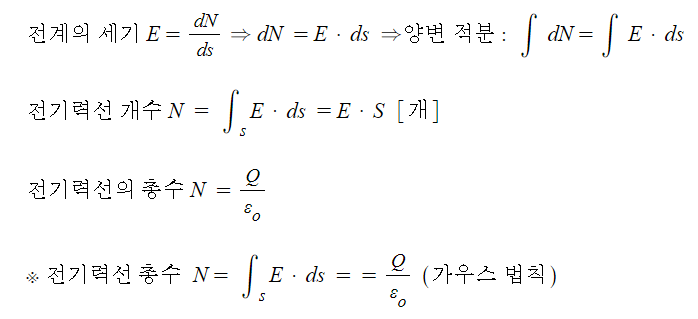

가. 면적분과 체적적분의 변환에 관계를 나타낸다.
나. 임의의 폐곡면의 표면을 뚫고 나오는 전기력선의 총수는 이 폐곡면에 둘러 쌓여진
체적속에서 빠져 나오는 전기력선의 총수와 같다.
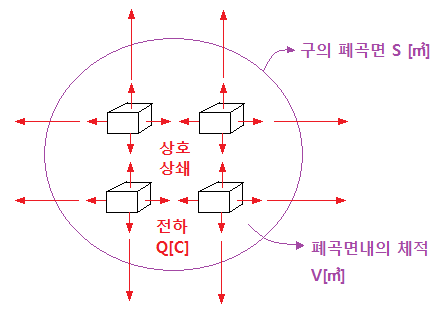
※ 단위 체적당 전기력선의 수를 면당 1개로 가정한다면 단위 체적 내부에서는 상호
전기력선이 상쇄되고 바깥면에서만 전기력선이 나오게 된다.
따라서 구의 내부에서는 전기력선이 발생하지 않게 되며 이로 인해서
구의 체적내에서 나오는 전기력선의 수와 구의 바깥면에서 나오는 전기력선의 수는
같게 된다.
① 면에서 빠져 나가는 전기력선의 총수

② 체적에서 빠져 나가는 전기력선의 총수
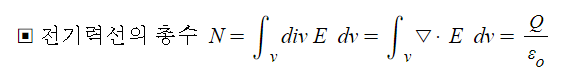

| 전자기학 핵심요약 정리 - 전기기사 (0) | 2023.04.29 |
|---|---|
| 가우스 정리, 포아송 방정식, 라플라스 방정식, 공식정리 (2) | 2021.11.14 |
| 전속과 전속밀도 (0) | 2021.11.11 |
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
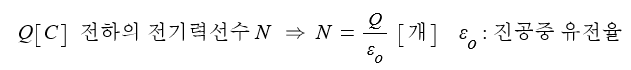
▣ 전기력선의 수는 유전율에 의하여 결정되므로 매질에 따라 유전율이 달라지므로
전기력선의 수도 매질에 따라 달라지므로 전계를 분석하는데 어려움을 겪을 수 있다.
▣ 따라서 전계분석을 용이하게 하기 위하여 매질에 관계없이 Q[C]의 전하에서는
일정한 전기력선수가 나온다고 가정하는 전속(선)의 개념을 도입하게 된다.
※ 매질에 상관없이 전기력선의 수가 변하지 않는 선의 개념을 도입 ⇒ 전속선, 전속
① (매질에 상관없이) Q[C]의 전하에서 Q[개}의 전속선이 나온다고 가정한다.
전속과 전속선은 1[C]의 전하량을 하나의 단위로 삼은 것이다.
1[C] ⇒ 1[개] 전속선 / 5[C] ⇒ 5 [개]
1[C] 전하량에서는 전속과 전속선이 1이고 5[C] 전하량에서는 전속과 전속선이 5이다.
② 전속선의 수와 전하량 Q [C]가 같다.
③ 단위도 전하량과 같은 [C]을 사용한다.
▣ 공기중에서 반지름이 r[m]인 구 내부에 Q[C]의 전하가 있다.
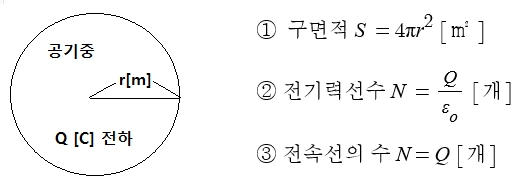
▣ 공간에서 중심에서 표면까지의 거리가 r[m]인 구의 표면적은 4πr^2으로 나타낼 수 있다.
이 때 표면적을 통해 나오는 전기력선의 개수는 전체 전하량을 유전율로 나눈 숫자가 될 것이다.
그러나 전속(전속선)의 숫자는 전하량 Q와 같게 된다.
▣ 전계의 세기는 단위 면적당 전기력선의 수와 같다.
⊙ 전계의 세기는 구 표면에서 나오는 전기력선의 밀도와 같으므로
전체 전기력선을 구의 표면적으로 나누어 산정하게 된다.
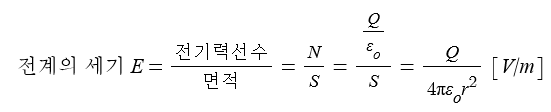
▣ 전속밀도는 1[C]의 전하에서 나오는 전속을 1전속으로 규정하고 단위면적당
전속수를 구하는 것으로 단위 면적당 몇 쿨룽[C]의 전하에 해당하는 전속이
나오는지를 구하는 것이다.

예제 : 공기중에 전하(Q)가 25π [C] 이 있을 때 이 전하로 부터 거리가 5 [m] 떨어진 곳에ㅅ서
나오는 전속, 전기력선의 수 (N), 전속밀도 (D), 전계의 세기 (E)를 구하시오.
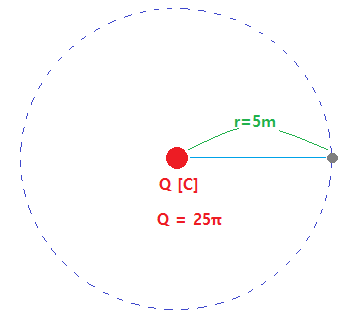
① 전속선수 = 전하량 Q = 25π = 78.5 [C]
▣ 전속선은 1[C]의 전하량을 1 전속으로 정의하므로 Q[C]의 전하에서는 Q개의 전속선이
25π의 전하량에서의 전속이나 전속선은 25π가 된다.
② 전기력선수
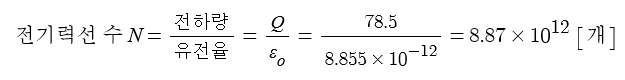
▣ 전기력선의 수는 전기력선은 1[m]의 1[V]의 전위량을 나타내는 전하량인 유전율로 전체 전하량을
나누어 산정하게 된다. 전기력선의 수는 1[m]에 1[V]의 전위차를 발생시킬 수 있는 전하량의 묶음이
얼마나 많이 있는가를 나타내는 것으로 보면 된다.
③ 전속밀도
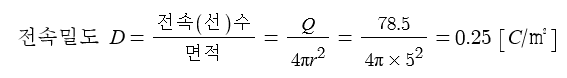
▣ 전속밀도는 단위 면적당 몇 [C]의 전하가 분포하는가를 나타내는 수치이다.
전속의 의미가 [C] 단위의 전하가 몇 묶음이 있는가를 나타내는 것이므로
단위 면적에 몇 [C]의 전하가 있는가를 나타내는 수치이다.
④ 전계의 세기 (전기력선의 밀도)
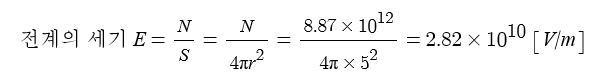
▣ 전계의 세기는 단위 면적당 전기력선의 수를 나타낸다.
⑤ 전속밀도 D
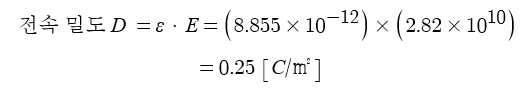
▣ 전속밀도는 단위 면적당 전속이 얼마나 있는가를 구하는 것이다.
전속이 1[C]에 해당하는 전하량이므로 전속밀도란 단위 면적당
몇 [C]의 전하가 있는지를 나타내는 값이라고 할 수 있다.
| 가우스 정리, 포아송 방정식, 라플라스 방정식, 공식정리 (2) | 2021.11.14 |
|---|---|
| 벡터의 적분, 발산 정리 - 전자기학 (0) | 2021.11.12 |
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
| 전자기학 - 전기력선, 등전위면, 도체, 벡터 미분 (0) | 2021.10.29 |
공기중의 전계의 세기를 구할 때 전하량을 유전율로 나누어 산정하게 된다.
유전율이 유전체가 전하를 품는 양이란 의미를 생각한다면
전계의 세기와 유전율의 관계를 이끌어 내기는 쉽지 않은 것 같다.
왜 전계의 세기를 구하는데 유전율의 개념을 끌어 들이고
총전하량을 유전율로 나누어 전계의 세기를 구하는지
차근차근 알아 보도록 하자.
전계의 세기 E는 공간중에 전하 Q[C]이 있을 때 이 전하로 부터 r [m] 떨어진 곳에
단위 양전하 +1[C]의 전하를 놓았을 때 이 단위 양전하에 미치는 힘의 세기를 말한다.
전계의 세기 E는 다음과 같이 표현한다.
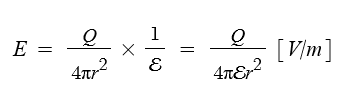
전계의 세기는 영향을 미치는 전하 Q로 부터 r[m] 떨어진 곳의 전계의 세기이므로 쿨룽의 법칙
에서 두전하량의 곱 Q × 1이므로 전하량은 Q가 되며 전하량은 거리 제곱에 반비례하게 되며
점전하 이므로 구의 표면적 4π로 나누어 산정하게 되며 여기에서 유전율 ε으로 나눠준다.
여기서 전계의 세기 E는 Q[C]의 점전하로 부터 r[m] 떨어진 점에 +1[C]의 양전하를 놓았을 때
이 단위 양전하에 영향을 미치는 전하량으로도 표현할 수도 있다.
위 식을 세분하여 보면 전계의 세기 E에 영향을 미치는 요인은 두가지로 나누어 볼 수 있다.
먼저는 전하 Q로 부터의 거리이다. 거리 r이 얼마만큼 떨어져 있느냐에 따라서
해당 등전위면의 구의 표면적은 결정된다. 구의 표면적에 따라 전계의 세기에 영향을 주는
전계의 발산량이 결정되게 된다. 또하나는 유전율에 따라 영향을 받게 된다.
유전율은 1[m] 거리에 1[V]의 전위차를 발생시키기 위해 필요한 전하량으로 생각하면 쉽다.
전계의 세기는 단위 면적당 전위경도를 의미하므로 전계의 세기를 계산하기 위해서는
전체 전하량을 유전율로 나눠주게 된다.

Q[C]의 점전하를 원점으로 하는 반지름 r[m]의 구체표면으로 나눈 양과 같으므로
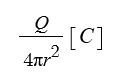
이 된다
이때, 이 전하가 놓여 있는 매질의 유전율이 ε [F/m]라 함은
그 매질 1[m]당 1[V] 의 전위차를 발생시키는데 ε[C]의 전하량을
필요로 한다는 의미이다
따라서 유전율이 ε[F/m]인 매질내에 놓여 있는 Q[c]의 점전하로 부터
r[m] 떨어진 지점에 도달한 전하들이 해당 지점에 영향을 미치는 힘의 세기인
전계의 세기는 해당 지점에 영향을 미치는 전하 즉

이 처럼 유전율로 나눠주게 되면
1[m] 당 전위차를 발생시키는 힘(세기)를 갖는다는 의미,
전계의 정의의 의미와 같게 된다.
종합하면, 유전율이란 그 매질이 전하를 품는 정도, 즉 1[m] 당 1 [V]의 전위차를
내기 위해 필요한 전하의 양이다.
전계의 세기란 어떤 전위차를 발생시킬 수 있는가를 나타내는 것이다.
따라서 전계의 세기를 나타낼 때에는 전계의 세기가 전하량과 비례하므로
전하량에 따라 전계의 세기가 달라지므로 유전율 즉 1[m]에 1[V]의 전위차를
발생시키기 위한 전하량인 유전율로 나누어 산정하게 된다.유전율이 높으냐, 낮으냐에 따라 전계의 세기는 달라지게 된다.진공중에서는 유전율이 낮으므로 아주 적은 전하량 만으로도
큰 전위차를 만들어 낼 수 있다.
| 벡터의 적분, 발산 정리 - 전자기학 (0) | 2021.11.12 |
|---|---|
| 전속과 전속밀도 (0) | 2021.11.11 |
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
| 전자기학 - 전기력선, 등전위면, 도체, 벡터 미분 (0) | 2021.10.29 |
| 전자기학 - 전위 [V] (0) | 2021.10.27 |
예제1 : V = 3x2y - y3z2 일 때 grad 의 점 (-1, -2, -1)에서의 값은 ?
※ 전위 경도를 구하라는 문제로서 grad는 편미분을 하라는 의미이다.
따라서 먼저 전위 V에 대하여 편미분을 하게 되고
편미분을 하고 난 후에 한점의 좌표값을 넣어 계산을 하면 된다.

▣ 전위 V에 대하여 편미분을 하였다. 전위 V를 x, y, z 축에 대하여 편미분을 하였다.

※ 위에서 편미분한 식에 대하여 점의 좌표값을 대입하여 최종값을 산정하였다.
예제2 : 전위함수 V = 2x+5yz+3 일 때 점 (2,1,0) 에서의 전계의 세기는 ?
※ 먼저 숙지해야 할 사항 : 전계의 세기 " E = - grad V " 이다.
전계의 세기는 마이너스(-) 전위경도 이므로 전위함수에 대하여
우선 편미분을 하게 된다. grad는 경도, 기울기를 의미하며 연산자는
편미분 연산자 즉 ▽을 적용하게 된다.

▣ 발산은 기호로 div 즉 diversions를 말하며 연산기호는 ▽· 이다.
발산은 편미분 연산자와 내적의 합성으로 결과값은 스칼라값이 된다.
▣ 발산의 계산, 산정방법
① 어떤 벡터 A가 있을 때 div A (▽·) 가 있을 때는
② 단위 체적당 발산하는 전기력선의 수를 계산하는 것임
A = Axi + Ayj + Azk 에 대하여 발산(div A), ▽· 를 구하라.

※ ▽· 는 계산 대상과 편미분 연산자를 내적하라는 의미로 보면 된다.
※ · (도트) 내적은 같은 성분끼리의 내적만 존재한다.

※ 내적의 곱은 스칼라값으로 나온다.
⇒ i, j, k 가 없다.
예제1. 벡터 A = x2i + y2j + z2k 일 때 점 (1,2,3) 에서 발산을 구하시오.
※ 발산 : div = ▽· ⇒ ▽ · A
▣ 발산 div를 구하라는 말은 계산 대상과 편미분 연산자를 내적하라는 말이다.
따라서 편미분 연산자 ▽과 벡터 A를 내적하게 된다.

예제2. 전계 E = 3x2i + 2xy2j + x2yzk 일 때 div E를 구하라.
div = 발산 = ▽ · E
▣ 전계의 발산을 구하는 것은 전계를 편미분 연산자 ▽와 내적하라는 말이다.

※ 한점이 주어지면 점 (1,2,3)을 위 식에 넣어서 계산하면 된다.
① 어떤 벡터 A = Axi + Ayj + Azk 일 때
② rot A = curl A = ▽ × A
※ 외적의 결과는 벡터이다. i, j, k 가 있어야 한다.

rot, curl는 벡터의 회전값을 구하는 것으로 이는 벡터의 외적값을 구하는 것이다.
외적은 값은 성분끼리의 값은 "0"이므로 자신과 같은 성분값은 계산하지 않고
자신과 다른 성분의 값으로 연산을 하게 된다. x축 성분의 값을 계산하는 경우에는
rot와 curl 값을 구하는 방법은 ①방향으로 곱한 다음에 이를 ②방향으로 곱한 값을
빼주는 방식을 산정을 하게 된다.
예제 1. 벡터 A = xyi + yzj + zxk 일 때 점 (4, 5, 3)에서의 ▽×A를 구하시오.
▽ × 는 curl, rot 를 구하라는 말로 이는 편미분 연산자 ▽과 계산 대상자를
외적하라는 말이다. 외적을 할 때에는 성분이 같은 경우에는 결과 값이
'0'이 되므로 성분이 다른 값을 계산하게 된다.
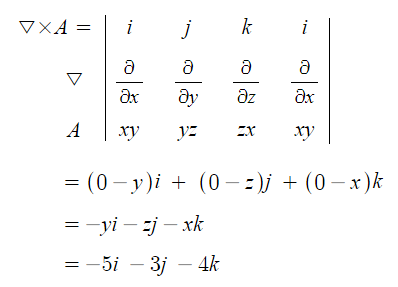
예제2. 벡터 A = xyz2i + xyzj + x2yzk 일 때 rot A를 구하면 ?
※ rot A = ▽ × A
rot 을 구하라는 의미는 편미분 연산자 ▽과 계산 대상을 벡터 외적하라는 의미이다.
외적을 할 때에는 성분이 같은 경우에는 결과 값이 '0'이 되므로 성분이 다른 값을
계산하게 되고 결과값은 벡터로 표시되게 된다.
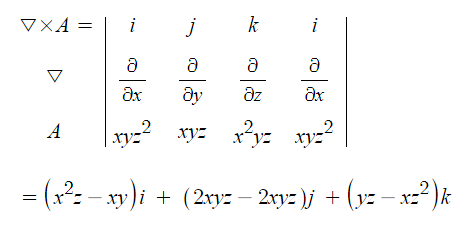
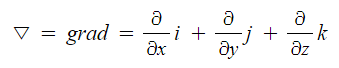
※ ▽ : 나블라, 델 - 편미분하라.
div 발산 = ▽· ⇒ 같은 성분 끼리만 내적한다.
※ i, j, k 가 없다.
rot = curl = ▽ × ⇒ 다른 성분끼리 외적한다.
※ i, j, k 가 붙는다.
| 전속과 전속밀도 (0) | 2021.11.11 |
|---|---|
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 전자기학 - 전기력선, 등전위면, 도체, 벡터 미분 (0) | 2021.10.29 |
| 전자기학 - 전위 [V] (0) | 2021.10.27 |
| 전계 및 전계의 세기 (0) | 2021.10.27 |
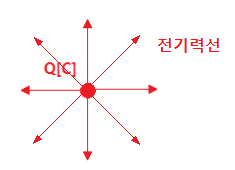
▣ 전기력선
⊙ 전계(E)내에서 단위 정전하 (+1[c])을 놓았을 때 이 단위 정전하가 받는
힘의 방향을 시각적으로 표현하기 위하여 가상한 선을 말한다.

가. 전기력선의 성질
① 전기력선은 양전하에서 시작하여 음전하에서 끝난다.

② 전하가 없는 곳에서는 전기력선의 발생과 소멸은 없다. (즉, 연속적이다)
③ 전기력선은 전위가 높은 곳에서 낮은 곳으로 향한다.

④ 두 전기력선은 서로 교차하지 않는다.
⑤ 전기력선은 그 자신만으로 폐곡선이 되지 않는다.
⑥ Q[C] 의 전하에서는 Q/εo 개의 전기력선이 나온다.

⑦ 전기력선의 밀도
⊙ 어느 점에서의 전기력선의 밀도를 그 점의 전계의 세기로 정의한다.
⊙ 전기력선이 어느 공간에 +1[C]의 양전하를 놓았을 때 받는 힘을 나타내기 위한 선이므로
이러한 전기력선이 얼마나 많이 있는지 적게 있는지를 나타내는 밀도는 전계의 세기를
나타낸다는 것은 당연한 말이다.

나. 전기력선의 방향
▣ 어느 점에서의 전기력선의 접선 방향을 그 점에서의 전계(E)의 방향으로 정의
※ 접선 : 수평방향, 법선 : 수직방향

⑨ 전기력선은 등전위면과 수직이다.
⑩ 전기력선은 도체 표면에 수직으로 출입한다.
⑪ 도체 내부에는 전기력선이 존재하지 않는다.
1. 등전위면
▣ 전계내에서 전위가 같은 점을 연결하여 얻어지는 면
⊙ 점전하로 부터 받는 힘의 세기는 그 점전하로 부터 거리의 제곱에 반비례하므로
등전위면은 점전하로 부터 같은 거리에 위치하게 된다.

가. 등전위면의 성질
① 서로 다른 전위를 가진 등전위면은 교차하지 않는다.
② 등전위면과 전기력선은 반드시 수직으로 교차한다.
③ 전기력선은 전위가 높은 곳에서 낮은 곳으로 향한다.
④ 등전위면은 폐곡면이다.
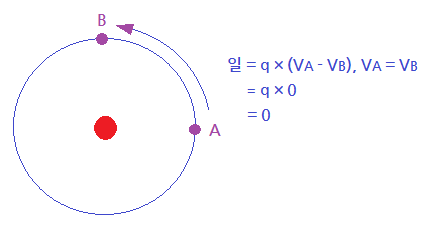
⑤ 등전위면을 따라 전하를 운반하는데 필요한 일은 영"0"이다.
① 대전된 도체의 전하는 도체 표면에만 존재한다.
※ 도체 내부에는 전하가 없다.
(대전체는 서로간 반발력이 작용하므로 밖으로 밀려나 바깥쪽에 대전체가 있다)
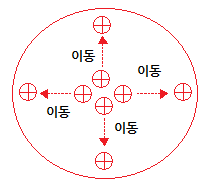
② 도체 내부의 "전계의 세기"는 "영(0)"이다.
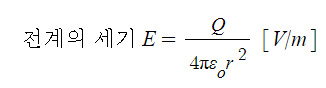
③ 도체 표면 및 내부의 전위는 등전위다.
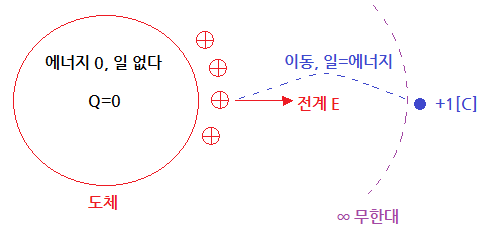
④ 도체 표면에서 전기력선은 도체표면에 수직으로 교차한다.
※ 도체 표면은 등전위면이다.
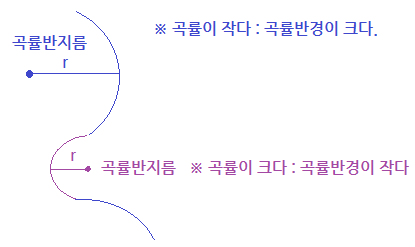
⑤ 도체 표면에서 전하밀도는 곡률반경이 클 수록 (곡률이 작을 수록) 작아진다
▣ 미분방정식은 다음과 같다.

미분
▣ 변수와 미분계수가 같을 때만 미분이 가능하다.

▣ 미분의 기본방식은 다음과 같다.


▣ 편미분 : 미분계수와 변수가 다른 경우에도 미분을 가능하게 한다.
① 변수와 미분계수가 달라도 미분이 가능하다.
② 다변수 함수에서 한개의 변수에 대해서만 미분을 한다.
③ 미분계수와 상관없는 변수들은 상수 취급을 한다.
④ 나머지는 "일반미분"과 같다.
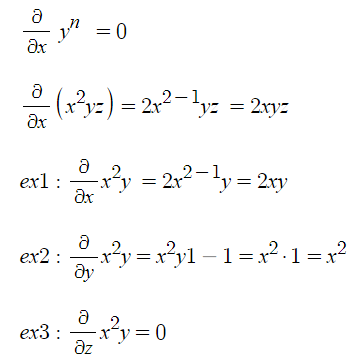
가. ▽
① 명칭 : "나블라", "del 델" ⇒ 편미분 연산자
② 표현

③ 결과 : 벡터 ⇒ i, j, k 로 표현
나. grad
① 명칭 : gradient
② 의미 : 기울기, 경사, 경도, 구배
③ 용도 : "전위 V"의 기울기를 구할 때
④ 표현 : " ▽"와 같다.
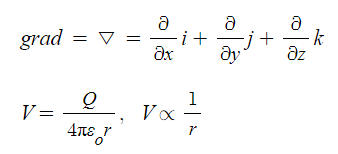
다. div
① 명칭 : 다이버젼스 divergence
② 의미 : 발산
③ 용도 : 전기력선이 발산하는 모양을 수식화할 때 사용
④ 표현 (연산자) : ▽ · (나블라 도트)
⑤ 결과 : 스칼라
라. rot, curl, Rotation
① 명칭 : 로테이션, 커얼
② 의미 : 회전 (Rotation)
③ 용도 : 자속이 회전하는 모양을 나타낸다.
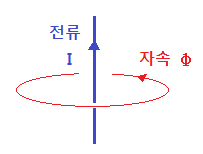
④ 표현 (연산자) : ▽ × (나블라 크로스)
⑤ 결과 : 벡터 i, j, k 로 표현
① ▽, grad, rot (curl) ⇒ 벡터 : 방향을 나타내는 i, j, k 로 표현
② div (▽·) ⇒ 스칼라 (내적)
가. 스칼라 기울기 = 전위의 기울기

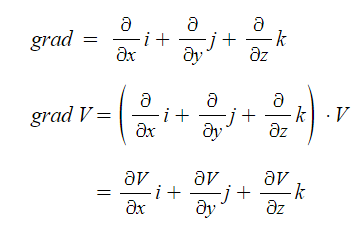
예제1. 전위함수 V = x^2yz 일 때 한점 (1,2,3)에서 grad V를 구하시오.
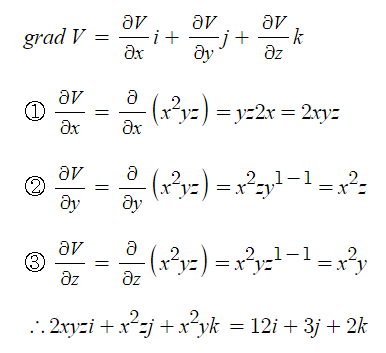
| 유전율과 전계의 세기 (0) | 2021.11.11 |
|---|---|
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
| 전자기학 - 전위 [V] (0) | 2021.10.27 |
| 전계 및 전계의 세기 (0) | 2021.10.27 |
| 대전, 대전체, 쿨룽의 힘 (5) | 2021.10.27 |
▣ 전위는 일의 다른 표현이다. 일은 특정 힘으로 대상물을 옮긴 거리로 볼 수 있다.
즉, 일은 힘 × 이동한 거리로 표현할 수 있다.
▣ 전위를 설명하기 전에 우선 "일"에 대하여 알아 보자


▣ 전위 : 전계의 세기가 E인 평등전계내에서 P점의 전위란 ?
⊙ 무한 원점으로 부터 단위 점전하(+1[C])를 전계에 대항하여 P점까지 이동시키는데
소요되는 일 (힘 × 이동거리)

▣ 전위란 위 그림과 같이 무한원점에 있는 +1[C] 전하를 P점으로 옮기는데 소요되는 일이
다. 전위를 구하기 위하여 힘과 거리로 나누어 일량을 구해 보자.

【 기본 적분식 】
▣ 전자기학 공부에 필요한 기본적분식에 대하여 알아보자.

▣ Q[C] 전하로 부터 r[m] 떨어진 지점의 전위는 ?


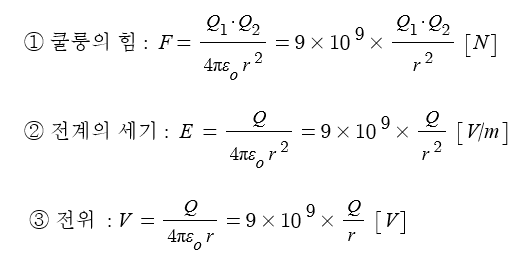
▣ 전위차 : +1 [C]의 단위전하를 B점에서 A점으로 이동하는데 소요되는 일
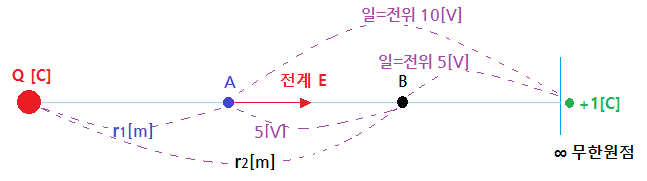
▣ 위 그림에서 전위차는 VA와 VB의 전위의 차이를 말하는 것으로 +1[C]의 단위전하를
B점에서 A점으로 옮기는데 소요되는 에너지(일)를 말한다.
⊙ 전위차 VAB = VA - VB
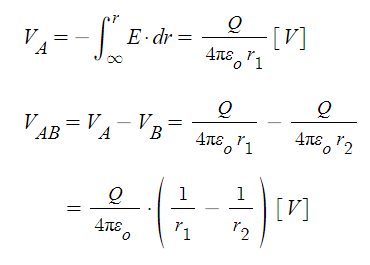
나. A,B점 사이에 q[C]을 이동시킬 때 소요되는 일
▣ B점에서 A점으로 +1[C]의 단위 전하를 이동하는데 소요되는 일이 전위이므로
B점에서 A점으로 q[C]을 옮기는데 소요되는 일은 전위차 × q[C]이 된다.

다. 전위의 기준

① 전위의 기준은 "무한원점"을 기준으로 한다.
② 무한원점의 전위는 "0" 전위이다.
※ 일 = 힘 × 이동한 거리 = +1[C] × "0" = "0"
▣ Q[C]의 전하에 의하여 만들어진 전계내에서 단위 정전하를 폐회로에 따라 일주
시킬 때 "전계 E가 하는 일"은 "영(0)"이다.
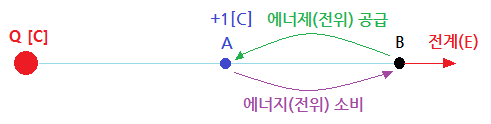
※ 정전하가 이동하여 제자리로 돌아 오면 이동하면서 소비된 에너지 만큼 제자리로
돌아 오기 위해서는 전위를 외부에서 공급받아야 하므로 결국 소요된 전위(에너지)는
없게 된다.
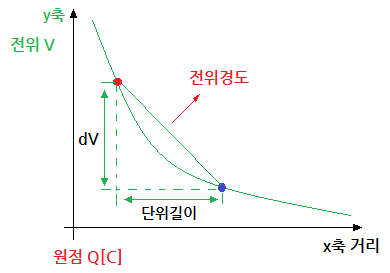
가. 전위의 경도 (전위의 기울기)
※ 기울기를 구하라는 말은 미분하라는 말과 같다.
⇒ 단위 길이당 전위의 변화
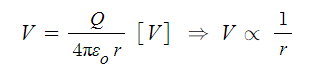

【 종합정리】
전계 E = - grad V (전위의 기울기) - 는 방향이 반대라는 의미이다.
※ 전위의 경도는 전계의 세기와 크기는 같고 방향이 반대라는 의미이다.
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
|---|---|
| 전자기학 - 전기력선, 등전위면, 도체, 벡터 미분 (0) | 2021.10.29 |
| 전계 및 전계의 세기 (0) | 2021.10.27 |
| 대전, 대전체, 쿨룽의 힘 (5) | 2021.10.27 |
| 정전계, 전자유도, 쿨룽의 법칙 - 전자기 (0) | 2021.08.25 |