Darcy's Law : 달시의 법칙
1856년 프랑스인 다르시(H. Darcy)가 여과사(濾過沙)의 실험에서 발견한 법칙으로
한마디로 말하면 모래로 가득 채운 원통에 물을 통과시키는데 필요한 압력과 원통의 길이와의 관계를 나타내는 식을 말한다.
즉, 다공성 매질(모래)를 통과하는 수량(물의 양)이 압력과 원통의 길이에 따라 얼마나 달라 지는가를 나타내는 식이다.
다르시는 모래 내부에서 물의 움직임을 규명하기 위해 실험을 하였다.
시간(t) 동안 모래 단면적 A를 통하여 흐른 물의 체적(수량, Vol), 수두(水頭, h1과 h2)를 측정한 결과 물의 체적(수량, Vol)과 다른 요소들 사이에는 일정한 관계법칙이 있음을 발견하였다.
Darcy는 모래층을 통과하는 물의 유동을 연구하던 중에 모래층을 통과하는 물의 유량 Q는 모래층의 지점1의 수두 h1과 지점2의 수두 h2의 차에 비례하고, 1, 2 지점간의 거리 L에 반비례하며, 단면적 A와 매질의 성질에 따라 좌우되는 계수 K 즉, 수리전도도에 비례함을 알아 냈다.
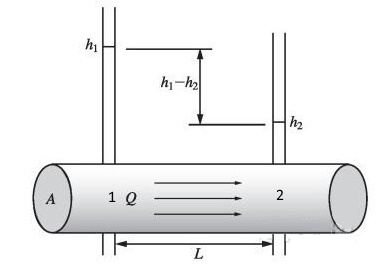
다르시의 법칙은 다공성 매질을 통과하는 유체의 단위 시간당 유량과 유체의 점성, 유체가 흐르는 거리와 그에 따른 압력 차이 사이의 비례관계를 보여준다. 유체로 포화된 다공성 물질(多孔性物質) 매체 속을 통과하는 수량(水量)은 수두손실(水頭損失)에 비례하고 통과하는 매체의 거리에 반비례한다는 것을 보여준다.
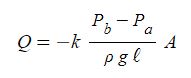
유량 Q (㎥/s)는 매질의 투과율 (Permeability, K), 물이 흐르는 매질의 내부 단면적 A과 유체가 흐르는 두 점간 압력차이 (Pb - Pa)의 곱을 유체가 흐르는 길이(ℓ)로 나눈 것과 같다. 음의 기호는 압력이 낮아지는 방향으로 유체가 흐른다는 것을 의미한다.
여기서 투수계수는 유체의 점성, 매질의 특성 (흙 입자의 크기와 모양, 배열 상태, 포화도,
간극비 등)과 관련 되어 정해지는 값이다.
적용범위
다르시의 법칙은 유속이 느린 점성 흐름에 대해서만 유효한데 대부분의 흐름에는 다르시의 법칙을 적용할 수 있다. 일반적으로 레이놀즈 수가 1보다 작은 흐름은 층류이고 다르시의 법칙을 적용할 수 있으며 실험에 의하면 레이놀즈수가 약 10 정도인 흐름까지도 다르시의 법칙을 적용할 수 있다.
#달시 #다르시 #유체 #손실수두 #유량 #압력 #매질 #투과율 #단면적 #길이 #레이놀즈
'소방설비기사 (기계) > 기초물리' 카테고리의 다른 글
| 특수 상대성 이론의 기본원리 : 마이컬슨-몰리실험, 상대성원리, 광속불변원리 (0) | 2024.08.20 |
|---|---|
| 열기관과 열효율 : 카르노기관, 영구기관 (0) | 2024.08.19 |
| 에너지 기본 개념 (위치 · 운동 · 내부 에너지, 엔탈피) (0) | 2024.08.15 |
| 열역학 제1·2법칙 : 에너지보존법칙, 가역과정 · 비가역 과정 (0) | 2024.08.14 |
| 열역학 제1법칙 (등적 · 등압 · 등온 · 단열과정) (0) | 2024.08.13 |
