1. 기체가 한일과 내부에너지
가. 열에너지
▣ 열에너지 : 물체 내부의 분자운동에 의해 나나타는 에너지
⊙ 온도 : 물체의 차갑고 뜨거운 정도를 기준을 정해 수치로 나타낸 것
⊙ 열 : 온도가 높은 물체에서 낮은 물체로 스스로 이동하는 에너지
▣ 열 평형상태 : 온도가 다른 두 물체가 접촉해 있을 때 두 물체의 온도가 같아지는 상태
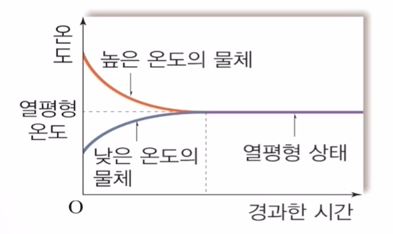
위 그림에서 온도가 높은 물체와 낮은 물체가 접촉하면 결국 열평형상태가 된다는 것을 보여 준다.
나. 기체가 하는 일
▣ 여기서 일은 물체가 힘 방향으로 이동하는 것을 말한다.
W = P · △ V [단위 : J]
여기서, W : 기체가 외부에 한 일
P : 압력
△V : 부피의 변화 (이동한 거리)
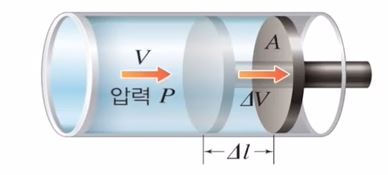
위 그림에서 압력은 기체가 벽면을 때리는 힘으로 보면 되는데 이 힘에 의하여 피스톤이 힘 방향으로 이동하게 되면 이를 일을 한 것으로 볼 수 있다. 즉, 일정한 압력일 때 부피를 증가시키면 일을 하게 된다. W = F · d 에서 W = P · △V 가 된다.
이 때 일이란 부피의 변화가 있어야 한다. 부피의 변화가 없다면 일을 한 것이 아니다.
▣ 기체의 부피 변화와 외부에 한 일의 관계
⊙ 기체가 팽창할 때 : △V > 0 이므로 W > 0 이다. ⇒ 기체가 외부에 일을 한다.
⊙ 기체가 수축할 때 : △V < 0 이므로 W < 0 이다. ⇒ 기체가 외부에서 일을 받는다.
▣ 압력과 부피의 관계 그래프
⊙ 기체가 한 일은 압력 - 부피 그래프 아랫부분의 넓이와 같다.

위 그래프에서 압력은 힘이고 부피는 이동거리이므로 P × V는 일의 양 W가 된다.
그런데 압력 - 부피 곡선이 직선일 경우 P × V는 직선 아래 부분 면적이 되므로 P - V 곡선 아래 부분 면적이 일의 양이 된다.
위 그림의 오른쪽 순환과정의 경우에는 순환과정 위 부분 곡선 아래 부분면적에서 아래 부분 곡선 아래 부분 면적을 뺀 면적이 일의 양이 되는데 이는 순환곡선 내부의 면적이 된다.
즉, 순환과정의 경우에는 순환곡선내부의 면적이 일의 양이 된다.
나. 기체의 내부 에너지
▣ 기체 내부 에너지 : 이상기체의 경우 내부에너지는 기체 분자운동에너지의 총합이다.
기체의 내부에너지는 열역할 제1법칙을 이해하는데 매우 중요한 개념이다. 내부에너지는 이상기체상태를 가정해서 알 아 볼 것인데 이상기체란 기체 분자간 힘을 거의 무시하는
상태를 말한다. 분자간 힘이 작용하지 않고 분자간 충돌이 일어나지 않는 상태를 말한다.
U ∝ N Ek ⇒ U ∝ NT
여기서, U : 이상기체 내부에너지
Ek : 분자의 평균 운동에너지
N : 기체 분자수
이상기체 내부에너지는 기체의 평균운동에너지에 비례하고 기체의 분자수와 절대온도의 곱에 비례한다. 즉, 기체의 내부에너지는 기체의 분자수와 절대온도에 의해 결정된다. 특히, 절대온도에 의해 내부에너지가 결정된다.
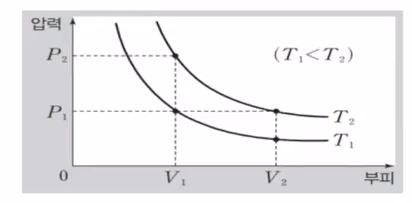
위 그림의 그래프는 등온선을 나타낸다.
등온선은 온도가 같은 점을 이은 선이다. 위 그래프에서 T1선과 T2선 상에 있는 점들은 온도가 같게 된다. 등온선의 특징중에 하나가 P × V 값이 같다. 따라서 동온선 내에서는 모두 P × V 값이 같고 동온선이 우상향하게 되면 P × V 값이 커지게 된다.
2. 열역학 제1법칙
Q = △ U + W = △U + P · △V
여기서, Q : 외부에서 가해지는 열량
△U : 기체 내부의 에너지 변화량
W : 기체가 외부에 한 일
P : 압력
△ V : 기체의 부피 변화량
위 식의 의미는 어떤 기체에 외부에서 열을 가해 주면 기체의 내부에너지를 증가시키거나 기체가 외부에 일을 할 수 있게 도와 준다라고 할 수 있다. 즉, 외부에서 받은 열이 기체의 내부에너지로 변화되거나 외부에 하는 일로 변환된다는 에너지 보존 법칙을 말한다.

위 그림의 실린더를 예를 들면 외부에서 열이 가해지면 실린더 내의 기체의 내부에너지는 증가하데 된다. 왜냐하면 실린더 내의 기체의 온도가 증가하기 때문이다. 또한 기체 내부에 증가한 에너지로 외부에 일을 할 수 있게 된다.
그런데 위 식에서 △U ∝ N · T 이다. 즉, 내부에너지는 기체의 분자수와 절대온도에 비례하게 된다.
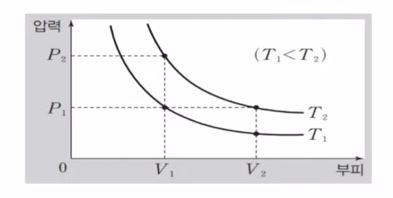
위 그래프에서 곡선은 동온선을 나타낸다.
이 등온선에서는 P × V 값이 같게 된다. 등온선에서는 온도가 같게 되는데 온도가 같다는 말은 내부에너지가 같다는 의미이다. 이는 기체 분자의 운동에너지도 같다는 것과 같다.
가. 등적 과정 (부피가 일정한 과정)
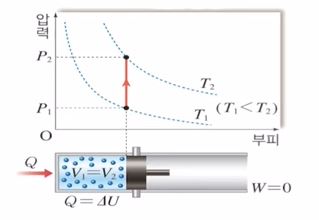
등적과정은 부피가 일정할 때의 과정을 말한다.
즉, 부피의 변화량 △V가 "0"일 때의 과정이다. 위 그림에서 실린더 내에 외부로 부터 열이 가해지는데 부피가 변화할 수 없는 상황이다.
Q = △U + P · △V 의 식에서 △V=0 이면 Q = △U 가 되므로 외부에서 가해준 열은 모두 내부에너지 증가로 변환된다.
위 그래프를 보면 부피가 변하지 않고 있다. T1 곡선에서 T2 곡선으로 올라가는 모습을 보여준다. 등온 곡선이 우측 상단으로 이동하였으므로 내부에너지는 증가하고 온도도 증가하고 압력도 증가하게 된다.
나. 등압과정 (압력이 일정한 과정)
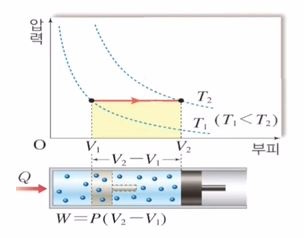
등압과정은 압력이 일정한 과정이다. 위 그림의 실린더를 보면 외부로 부터 열을 받고 부피가 증가하는 모습을 보여 준다. 식으로 표현을 하면 다음과 같다.
Q = △U + P · △V
위 식에서 압력이 일정하다고 하였으므로 P값이 일정하다. 외부에서 열이 가해지면 압력 P값만 제외하고 모두가 증가하게 된다. 외부에서 열이 전달되니 온도가 올라가서 내부에너지가 증가하게 되고 부피가 팽창하게 된다. 열이 들어 오면 내부 에너지가 증가하고 동일한 압력 내에서 부피가 증가하므로 외부에 일을 하게 된다.
위 그림의 그래프를 보면 압력은 일정한 상황이고 부피가 쭉 증가하게 된다. 압력 - 부피 그래프에서 그래프 아랫쪽 부분의 면적이 일의 양이 된다.
다. 등온과정 (온도가 일정한 과정)
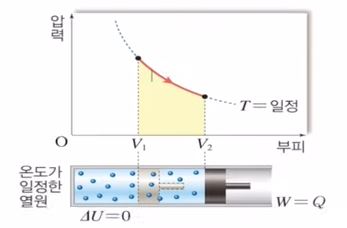
등온과정은 온도가 일정한 과정을 말하는데 위 그림에서 온도가 일정하다는 것은 동온선을 변화하는 과정을 말한다. 이를 식으로 나타내면 다음과 같다.
Q = △U + P · △V
위 식에서 외부에서 열을 받는데 온도가 일정하다 하였으므로 내부에너지의 변화량은 없게 된다. P · △V 는 일을 나타내는데 외부에서 받은 열이 모두 일로 변화한다는 것이다.
위 그래프를 보면 그래프 아래쪽 면적이 일의 양이 된다. 일을 할려면 부피가 증가해야 한다. 즉, 외부에서 열을 받아 부피가 증가하게 된다. 등온선은 P × V가 일정하다고 했다. 따라서 P × V 가 일정하려면 P·△V에서 부피가 증가해야 하므로 압력은 감소해야 한다.
종합하면 동온 과정에서는 내부에너지의 변화가 없으므로 외부에너지를 받은 만큼 일을 하게 된다. 압력은 감소하면서 부피가 증가하여 외부에 일을 하게 된다.
라. 단열과정
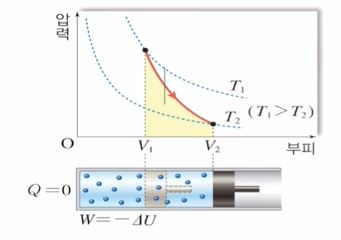
단열과정은 열의 출입이 없는 과정을 말한다. 즉, Q의 값이 변화가 없다. △Q = 0 인 상태를 말한다. 열량 즉, Q값에 변화가 없다. △Q = 0 인데 위 식에서 보면 부피가 증가하고 있다. 이를 식으로 나타내면 다음과 같다.
Q = △U + P · △V
위 식에서 Q는 변화가 없는데 부피가 증가하려면 내부에너지를 소모하면서 일을 해야 하는 과정을 말한다. 위 그림에서 그래프를 보면 내부에너지가 감소하므로 등온선이 아래로 떨어지게 된다. 이는 P × V 값이 감소함을 나타낸다. 따라서 부피는 증가하는데 P × V값이 감소하므로 압력 P값은 감소해야 된다.
이를 종합하면 외부에 한 일 W = - △U 가 된다. 즉, 내부에너지를 소모하면서 일을 하는 과정을 나타낸다.
#에너지보존법칙 #열역학제1법칙 #열역학 #에너지 #열 #온도 #등온과정 #등적과정
#등압과정 #단열과정
'소방설비기사 (기계) > 기초물리' 카테고리의 다른 글
| 에너지 기본 개념 (위치 · 운동 · 내부 에너지, 엔탈피) (0) | 2024.08.15 |
|---|---|
| 열역학 제1·2법칙 : 에너지보존법칙, 가역과정 · 비가역 과정 (0) | 2024.08.14 |
| 응력 (Stress, σ), 응력의 측정 및 사용목적 (1) | 2024.08.12 |
| 응력 (Stress, σ)란 무엇인가 ? (0) | 2024.08.12 |
| 일반기체상수(R)와 특정기체상수(R')와의 관계 (0) | 2024.08.12 |
